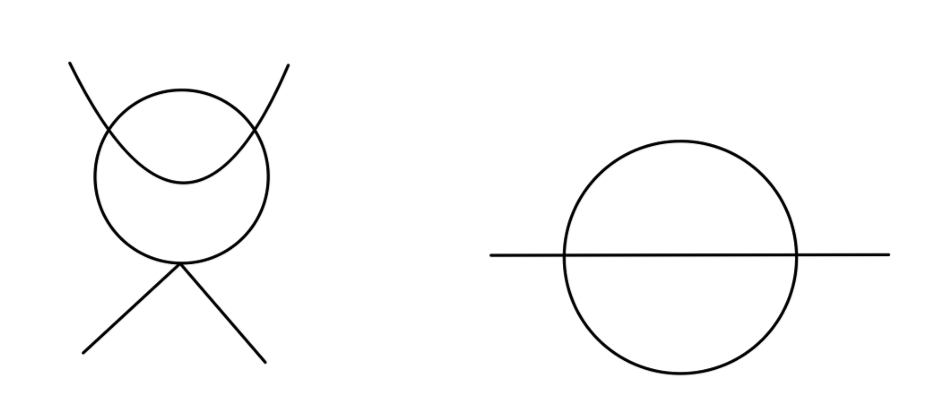高阶重整化微扰论

在上一篇中我们讨论了标量场以及 QED 的重整化理论，我们实际上提出了一套原则上可以计算到任意阶微扰论的方法。现在我们来进行一些更高阶的讨论。

当一个有限的图包含一个发散的子图时，对其的讨论是容易的。例如，我们将得到下两图的和是有限的：

我们可以预期进行外圈积分得到的结果会是收敛的。

但是有时候的情形就更为复杂一些，例如如下的 nested 或 overlapping 发散：其中两个发散的圈分享同一个传播子：

ϕ4\phi^4 理论

QED

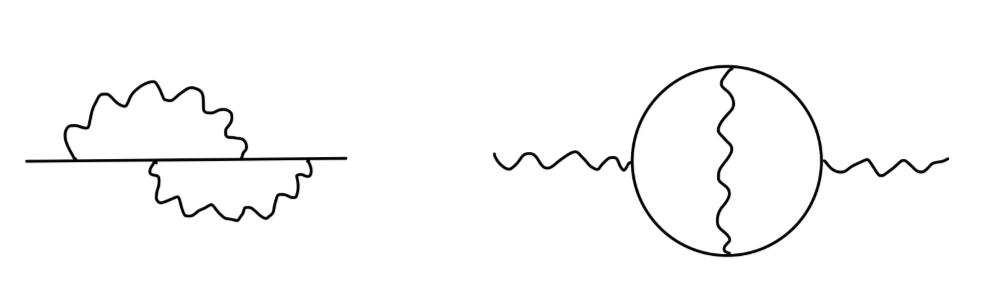
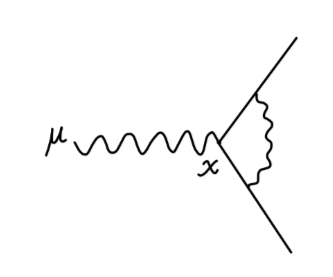
不妨以以下光子自能图为例：

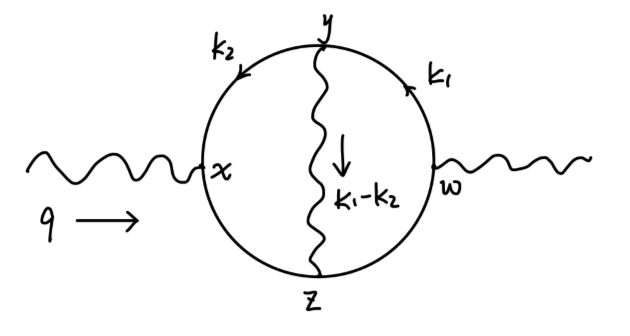
我们对上图进行一些基本的观察。我们根据费曼规则写出上式的值将包含两个圈动量 k1,k2k_1,k_2 的积分。我们先考虑动量 k1k_1 很大，而 k2k_2 很小的贡献，在动量空间中 k1k_1 的取值越大，将意味着在坐标空间中 x,y,zx,y,z 三个点越接近。因此此时的贡献可以看作对一阶光子自能图的一个顶点进行修正：

∼−ieγμ⋅αlog⁡Λ2\sim -ie\gamma^{\mu}\cdot \alpha \log\Lambda^2

得到光子自能图的值为：

∼α(gμνq2−qμqν)Π2(q2)⋅αlog⁡Λ2∼α(gμνq2−qμqν)(log⁡Λ2+log⁡q2)⋅αlog⁡Λ2\begin{aligned} \sim & \alpha(g^{\mu\nu}q^2 - q^{\mu}q^{\nu})\Pi_2(q^2)\cdot \alpha \log \Lambda^2\\ \sim & \alpha(g^{\mu\nu}q^2 - q^{\mu}q^{\nu})(\log \Lambda^2 + \log q^2)\cdot \alpha \log \Lambda^2\\ \end{aligned}

其中 log⁡Λ2\log\Lambda^2 项的贡献来自于 k1k_1 很大，k2k_2 也很大的区域。log⁡q2\log q^2 项的贡献来自于 k1k_1 很大，k2k_2 很小的区域。同样的项还来自于对光子自能图另一个顶点的修正。新出现的发散项：Π2(q2)⋅log⁡Λ2\Pi_2(q^2)\cdot \log\Lambda^2，在表观发散度的评判标准中是难以理解的：在我们利用表观发散度对发散的估计中，只会出现有关 qq 的多项式形式的发散，我们将其称之为 local divergences。而对于这种非多项式形式的发散，我们称之为 nonlocal divergences。nonlocal divergence 在物理本质上是将 local divergence 的图嵌入一个不发散的图（相应的动量取值很小，自然这部分的贡献不会发散）中得到的。

如果这种描述确实反映了两阶光子自能图的发散情况，对于 k1k_1 很小 k2k_2 很大 或 k2k_2 很小 k1k_1 很大的区域，因为此时的发散是由顶点修正的子图产生的，我们可以对每个顶点分别引入 α\alpha 阶的 counterterms，在代入一阶的光子自能图，即通过以下 counterterms 消去：

考虑这两项 counterterms 之后，通过我们之前的分析得到，剩余的发散将是 local 的，这正对应于 k1k_1 与 k2k_2 均取值较大时的贡献，我们可以通过下列 counterterm 的 α2\alpha^2 阶的项消去：

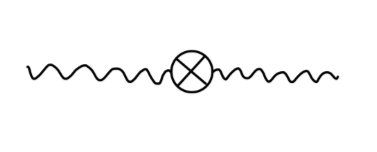
这种处理方法为我们提供了处理高阶费曼图的一种一般思路。对于一个给定的费曼图来说，其中可能包含 local divergences，这可以通过上一篇的方法消除（为 counterterms 添加相应的高阶项），而对于 nonlocal divergences，我们需要考虑这个发散的子图，将对应的顶点替换为 counterterms。这种做法能否消除 nonlocal divergences 并且保证计算出来的振幅是有限的呢？这个问题的答案是肯定的，称为 BPHZ theorem。

两圈图计算

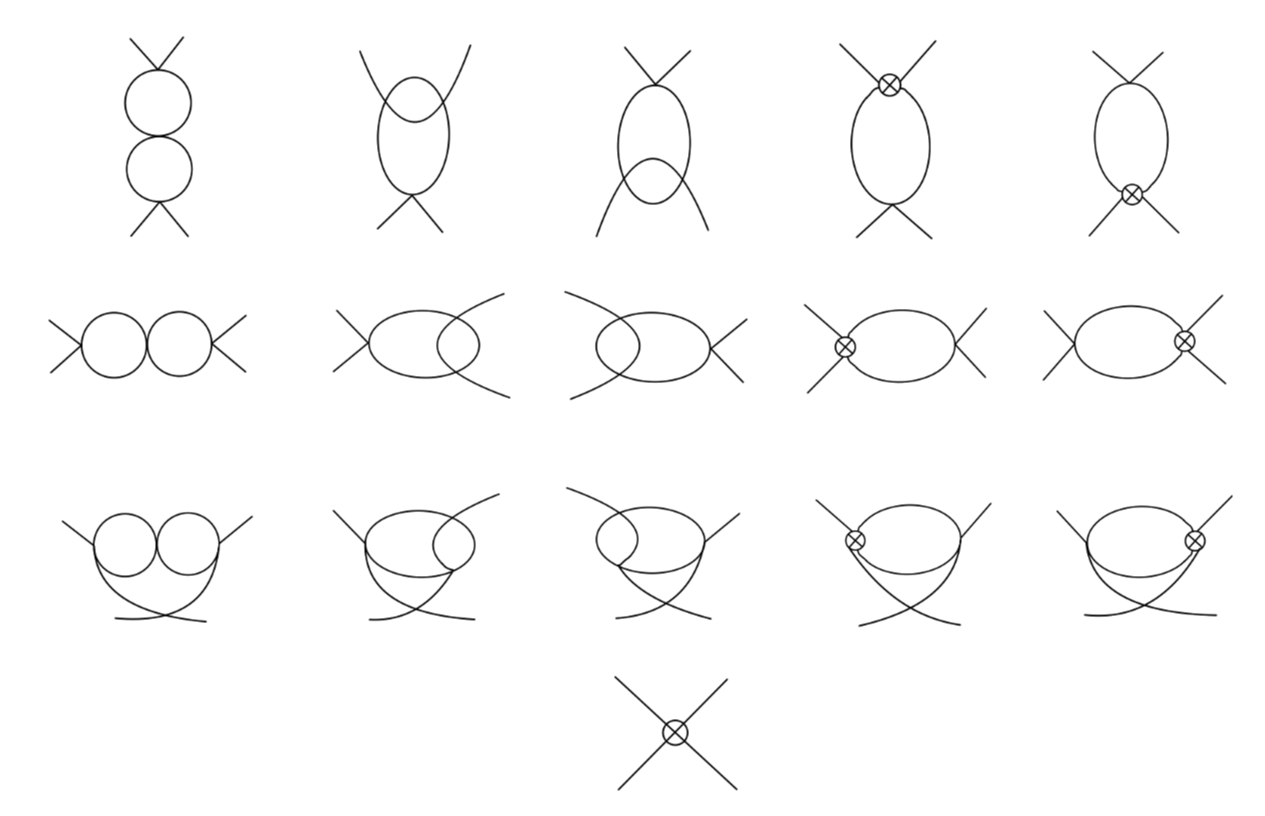
现在我们来举例说明高阶重整化微扰论，我们以 ϕ4\phi^4 理论的二阶圈图为例说明。有 1616 个相关圈图需要计算：

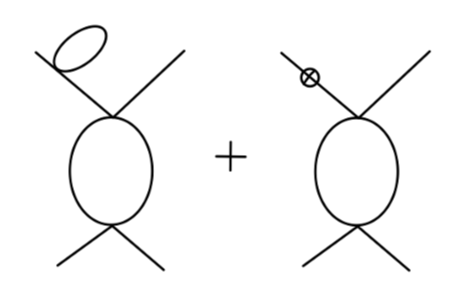
当然这里我们忽略了对传播子的一阶圈图修正的情况，因为这些图不难通过重整化消去，例如：

当然这 1616 个图通过 crossing symmetry 相关联。第一、二、三行分别为 ss-channel，tt-channel，uu-channel 的图。我们只需要先考虑 ss-channel 的图，再根据 crossing symmetry 就能够推广到 tt-channel 与 uu-channel 的情况。

因此我们考虑如下 ss-channel 的图：

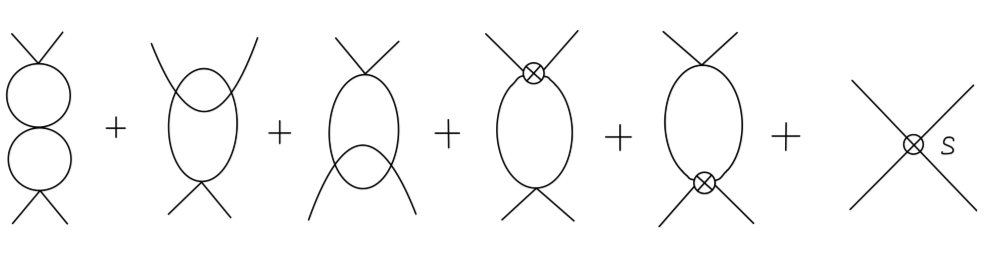
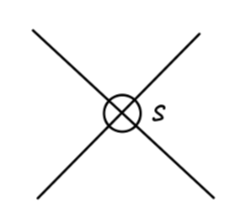
其中最后一项 counterterm 标有 ss 是指：该项 counterterm 仅仅代表对 ss-channel 部分的 O(λ3)\mathcal{O}(\lambda^3) 阶顶点修正。把 s,t,us,t,u 三个 channel 的图加起来才会得到完整的顶点 counterterm ：

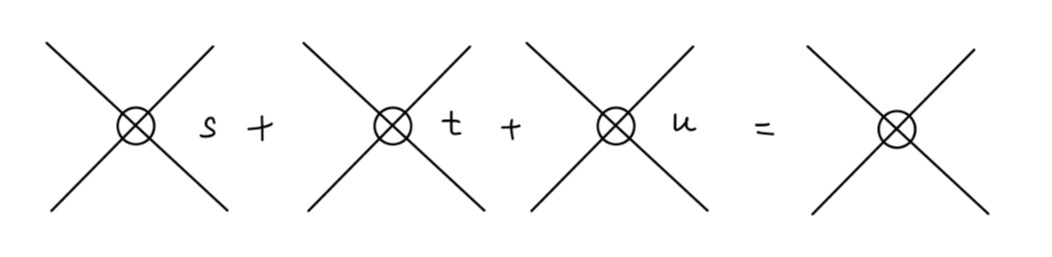
其中第四、五个图为：将顶点 counterterm 插入到一阶圈图中，这里的 counterterms 为 O(λ2)\mathcal{O}(\lambda^2) 阶顶点修正。我们先来回顾一下对 ϕ4\phi^4 重整化理论的一阶圈图计算：对于以下图

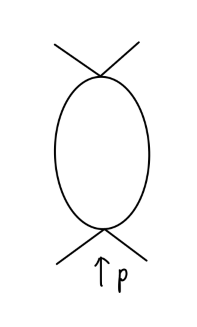
计算得到：

(−iλ)2⋅iV(p2)=(−iλ)2[−i2Γ(2−d2)(4π)d/2∫01dx1[m2−x(1−x)p2]2−d/2](1)\begin{aligned} &(-i\lambda)^2\cdot iV(p^2)\\ =&(-i\lambda)^2 [-\frac{i}{2} \frac{\Gamma(2-\frac{d}{2})}{(4\pi)^{d/2}} \int_{0}^{1} dx \frac{1}{[m^2-x(1-x)p^2]^{2-d/2}}]\\ \end{aligned}\tag{1}

根据重整化条件，得到 counterterms 的值为：

−iδλ=(−iλ)2[−iV(4m2)−2iV(0)](2)-i\delta_{\lambda} = (-i\lambda)^2[-iV(4m^2) - 2iV(0)]\tag{2}

我们将其分为 ss-channel 与 t,ut,u-channel 的贡献：

其值为：

(−iλ)2⋅−iV(4m2)(3)(-i\lambda)^2\cdot -iV(4m^2)\tag{3}

其值为：

(−iλ)2⋅−2iV(0)(4)(-i\lambda)^2\cdot -2iV(0)\tag{4}

上述式子确定了 counterterms 在 O(λ2)\mathcal{O}(\lambda^2) 阶的取值。为了计算 ss-channel 的二阶顶点修正。我们将前五个图分为三组

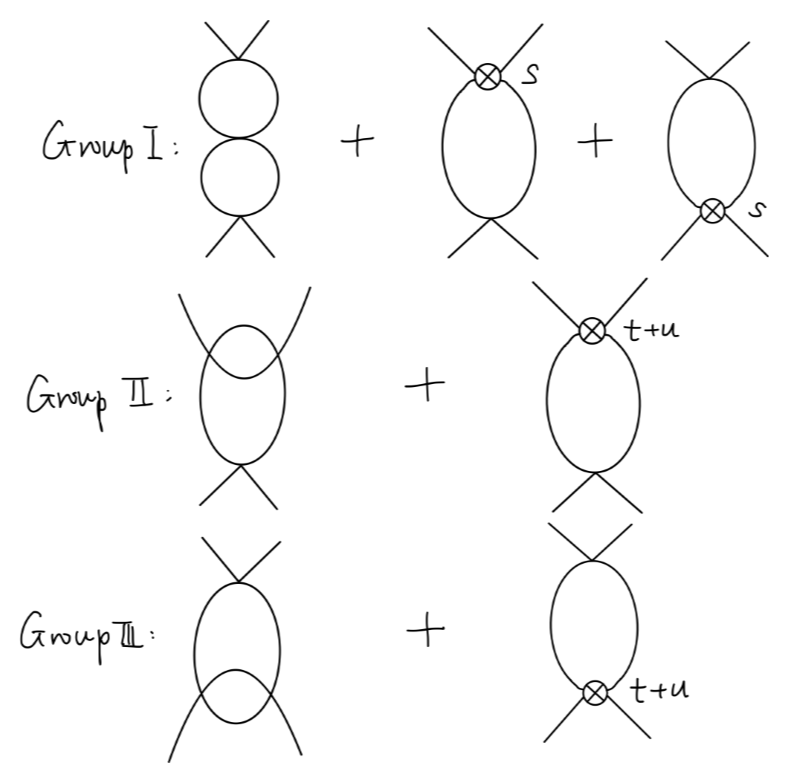
其中第二组与第三组通过交换初末态可以联系起来。直接计算第一组图是不难的：

其值为：

(−iλ)3⋅[iV(p2)]2(5)(-i\lambda)^3\cdot[iV(p^2)]^2\tag{5}

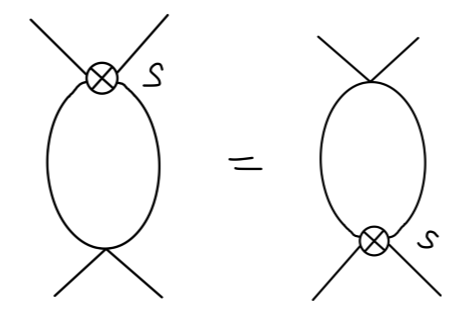
其值为：

(−iλ)3⋅iV(p2)⋅−iV(4m2)(6)(-i\lambda)^3\cdot iV(p^2)\cdot -iV(4m^2)\tag{6}

以上三个图相加得到：

(−iλ)3⋅[iV(p2)]2+(−iλ)3⋅iV(p2)⋅−iV(4m2)=(−iλ)3(−[V(p2)−V(4m2)]2+[V(4m2)]2)\begin{aligned} &(-i\lambda)^3\cdot[iV(p^2)]^2 + (-i\lambda)^3\cdot iV(p^2)\cdot -iV(4m^2)\\ =& (-i\lambda)^3(-[V(p^2) - V(4m^2)]^2 + [V(4m^2)]^2) \end{aligned}

其中 V(p2)−V(4m2)V(p^2) - V(4m^2) 为一个有限值，这是我们在一阶圈图中计算得到结果：

V(p2)−V(4m2)=132π2∫01dxlog⁡(m2−x(1−x)p2m2−x(1−x)4m2)(7)V(p^2) - V(4m^2) = \frac{1}{32\pi^2}\int_{0}^{1}dx \log(\frac{m^2 - x(1-x)p^2}{m^2 - x(1-x)4m^2})\tag{7}

那么仅剩的发散项为 [V(4m2)]2[V(4m^2)]^2，其不依赖于动量，我们可以将其吸收进 O(λ3)\mathcal{O}(\lambda^3) 阶顶点 counterterm 中去。

现在来考虑第二组。对于以下图：

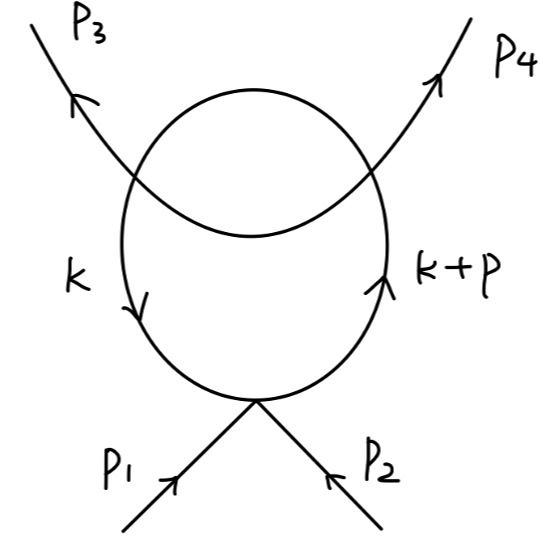
其值为：

(−iλ)3∫ddk(2π)dik2−m2i(k+p)2−m2iV((k+p3)2)(-i\lambda)^3 \int \frac{d^dk}{(2\pi)^d} \frac{i}{k^2-m^2} \frac{i}{(k+p)^2 - m^2} iV((k+p_3)^2)

使用费曼参数化得到：

−λ32⋅Γ(2−d2)(4π)d/2∫01dx∫01dy∫ddk(2π)d1[k2+2yk⋅p+yp2−m2]2×1[m2−x(1−x)(k+p3)2]2−d2\begin{aligned} -\frac{\lambda^3}{2}\cdot \frac{\Gamma(2-\frac{d}{2})}{(4\pi)^{d/2}} \int_{0}^{1}dx\int_{0}^{1}dy\int\frac{d^dk}{(2\pi)^d} &\frac{1}{[k^2 + 2yk\cdot p + yp^2 - m^2]^2}\\ \times & \frac{1}{[m^2-x(1-x)(k+p_3)^2]^{2-\frac{d}{2}}} \end{aligned}

现在继续将这两个分母结合在一起。利用以下公式：

1AαBβ=∫01dwwα−1(1−w)β−1[wA+(1−w)B]α+βΓ(α+β)Γ(α)Γ(β)\frac{1}{A^{\alpha}B^{\beta}} = \int_{0}^{1}dw\frac{w^{\alpha-1}(1-w)^{\beta-1}}{[wA + (1-w)B]^{\alpha+\beta}}\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}

将结果写为：

−λ32⋅Γ(4−d2)(4π)d/2∫01dx∫01dy∫01dw∫ddk(2π)d×w1−d2(1−w)(w[m2−x(1−x)(k+p3)2]+(1−w)[m2−k2−2yk⋅p−yp2])4−d2\begin{aligned} &-\frac{\lambda^3}{2}\cdot \frac{\Gamma(4-\frac{d}{2})}{(4\pi)^{d/2}} \int_{0}^{1}dx\int_{0}^{1}dy\int_{0}^{1}dw\int\frac{d^dk}{(2\pi)^d}\\ &\quad\times \frac{w^{1-\frac{d}{2}}(1-w)}{(w[m^2-x(1-x)(k+p_3)^2] + (1-w) [ m^2-k^2-2yk\cdot p -yp^2 ])^{4-\frac{d}{2}}} \end{aligned}

将完全平方式补齐之后，得到的分母形式为：

−[(1−w)+wx(1−x)]l2−P2+m2-[(1-w) + wx(1-x)]l^2 - P^2 + m^2

其中 ll 是 shift 后的动量，PP 是关于 p,p3p,p_3 的一个复杂函数。我们并不关心 PP 的具体取值，除了在 ω→0\omega \rightarrow 0 时，此时近似有：

P2(ω)=y(1−y)p2+O(w)P^2(\omega) = y(1-y)p^2 + \mathcal{O}(w)

完成对 ll 的积分，得到：

−iλ32(4π)d∫01dx∫01dy∫01dww1−d2(1−w)[1−w+wx(1−x)]d/2Γ(4−d)(m2−P2)4−d(8)-\frac{i\lambda^3}{2(4\pi)^d}\int_{0}^{1}dx\int_{0}^{1}dy\int_{0}^{1}dw \frac{w^{1-\frac{d}{2}}(1-w)}{[1-w+wx(1-x)]^{d/2}}\frac{\Gamma(4-d)}{(m^2-P^2)^{4-d}}\tag{8}

上述表达式除了有 d=4d=4 的极点外，还有 ω=0\omega = 0 的极点。我们将上式写为：

∫01dww1−d2f(w)(9)\int_{0}^{1}dw w^{1-\frac{d}{2}}f(w) \tag{9}

其中 f(w)f(w) 的具体形式在 (8)(8) 式中可以看出。为了单独讨论极点 w=0w=0 处的性质，我们将上式写为：

∫01dww1−d2f(w)=∫01dww1−d2f(0)+∫01dww1−d2(f(w)−f(0))(10)\int_{0}^{1}dw w^{1-\frac{d}{2}}f(w) = \int_{0}^{1}dw w^{1-\frac{d}{2}}f(0) + \int_{0}^{1}dw w^{1-\frac{d}{2}}(f(w)-f(0))\tag{10}

其中第二项为：

−iλ3Γ(4−d)2(4π)d∫01dx∫01dy∫01dww1−d2×((1−w)[1−w+wx(1−x)]d/21(m2−P(w)2)4−d−1(m2−P2(0))4−d)\begin{aligned} &-\frac{i\lambda^3 \Gamma(4-d)}{2(4\pi)^d}\int_{0}^{1}dx\int_{0}^{1}dy\int_{0}^{1}dw w^{1-\frac{d}{2}}\\ &\quad\times\big(\frac{(1-w)}{[1-w+wx(1-x)]^{d/2}}\frac{1}{(m^2-P(w)^2)^{4-d}} - \frac{1}{(m^2-P^2(0))^{4-d}}\big) \end{aligned}

相应的发散可以吸收进 O(λ3)\mathcal{O}(\lambda^3) 阶的顶点 counterterm 中。对于 (10)(10) 式中第二项，当 d→4d\rightarrow 4 时为：

−iλ32(4π)d(2ϵ)∫01dyΓ(ϵ)[m2−y(1−y)p2]ϵ⟶d→4−iλ32(4π)4(2ϵ)∫01dy(1ϵ−γ+log⁡(4π)−log⁡[m2−y(1−y)p2])(11)\begin{aligned} &-\frac{i\lambda^3}{2(4\pi)^d}(\frac{2}{\epsilon})\int_{0}^{1}dy \frac{\Gamma(\epsilon)}{[m^2-y(1-y)p^2]^{\epsilon}}\\ & \underset{d\rightarrow 4}{\longrightarrow} -\frac{i\lambda^3}{2(4\pi)^4}(\frac{2}{\epsilon})\int_{0}^{1}dy(\frac{1}{\epsilon} - \gamma + \log(4\pi) -\log[m^2-y(1-y)p^2]) \\ \end{aligned}\tag{11}

我们发现其中出现了对数项与 2ϵ\frac{2}{\epsilon} 相乘的 nonlocal divergence。

再计算以下 counterterm：

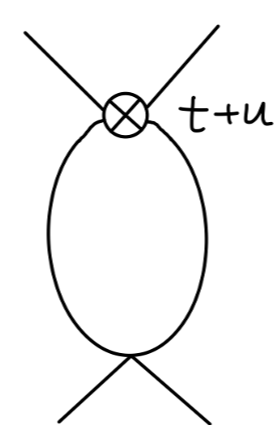
其值为：

(−iλ)3⋅−2iV(0)⋅iV(p2)=iλ32(4π)d∫01dyΓ(2−d2)[m2]2−d/2Γ(2−d2)[m2−y(1−y)p2]2−d/2⟶d→4iλ32(4π)4∫01dy(2ϵ−γ+log⁡(4π)−log⁡m2)×(2ϵ−γ+log⁡(4π)−log⁡[m2−y(1−y)p2])(12)\begin{aligned} &(-i\lambda)^3\cdot -2iV(0)\cdot iV(p^2)\\ =& \frac{i\lambda^3}{2(4\pi)^d}\int_{0}^{1}dy \frac{\Gamma(2-\frac{d}{2})}{[m^2]^{2-d/2}} \frac{\Gamma(2-\frac{d}{2})}{[m^2-y(1-y)p^2]^{2-d/2}}\\ \underset{d\rightarrow 4}{\longrightarrow} & \frac{i\lambda^3}{2(4\pi)^4} \int_{0}^{1}dy(\frac{2}{\epsilon} - \gamma + \log(4\pi) - \log m^2)\\ &\quad \times (\frac{2}{\epsilon} - \gamma + \log(4\pi) - \log[m^2-y(1-y)p^2]) \end{aligned}\tag{12}

将 (11)(12)(11)(12) 式相加，可以得到除了有限项与二阶极点 1/ϵ21/\epsilon^2 项，其中的 nonlocal 发散项将会消失，而二阶极点可以通过 O(λ3)\mathcal{O}(\lambda^3) 阶的顶点 counterterm 消去。最终我们将发现该散射振幅的有限项在 p→∞p\rightarrow \infty 时的行为：λ3log⁡2p2\lambda^3\log^2p^2。