原子核是多粒子体系,目前量子力学的方法对解决这类强相互作用的、粒子数目不是很大的多体问题还很困难。目前有关核结构的理论大多是半唯象的理论,即在实验基础上对原子核的某种模型进行假设,用来解释原子核的某些性质,它们指出了原子核内部运动的一些特点。除去半唯象模型理论外,核结构的微观理论也有很大发展:例如 Hartree-Fock 方法及其理论。本篇将介绍两种模型:壳模型与集体模型。
壳模型
幻数
对于原子来说,当核外电子数目为一定值时(2、10、18、36、54、86),原子特别稳定。同样的,实验发现:对于原子核来说,当质子数或中子数为 2、8、20、28、50、82,中子数为 126 时,原子核会特别稳定。这些数字被称为 幻数。由此启发:原子核是否也存在 壳层结构?
核素丰度是指核素在自然界中的含量。核素丰度是核素稳定性的一种标志。研究发现,中子数或质子数为幻数的核素的含量比附近核素的含量高的多。在利用液滴模型得到的原子核结合能公式中,在中子数或质子数为幻数时,实验与理论偏离最大,这表明这些原子核比一般原子核结合更加紧密。在 衰变中,也观察到了类似的现象。
壳模型
类比原子中电子的壳层结构,如果原子核中也存在类似于的壳层结构,则须满足以下条件:
- 在每一个能级上,容纳核子的数目应当有一定的限制。
- 核内存在一个平均场,对于接近于球形的原子核,这个平均场是一种有心场。
- 每个核子在核内的运动应当是各自独立的。
其中第一点是很好理解的:质子、中子也是费米子,满足泡利不相容原理。但第二、三点会让人费解:核中的核子密度很大,对应的核子在核中的平均自由程比核半径小很多,可以想象核子间似应不断发生碰撞,很难理解核子的运动是相互独立的。但液滴模型在解释幻数上无能为力,于是针对二、三点作一些解释:
-
原子核中虽然不存在与原子中相类似的不变的有心力场,但可以把每个核子的运动看成在一个平均场内运动。对于接近球形的原子核,可以认为这个平均场是一个有心场。
-
泡利不相容原理不但限制了同一能级所容纳核子的数目,更限制了原子核中核子与核子相互碰撞的概率。这使得核子在核内会有较大的平均自由程,单个核子能看做在核内独立运动。因此,壳模型也叫 独立粒子模型。
现在考虑选取中心势的形式,对比直角势能(认为核子从核的边界往外移动时所受向里的力会发生从极大到零的突变)和谐振子势能(核力的作用范围并不局限在核内),伍兹-萨克森(Woods-Saxon)势阱是一个合理的核场选择:
上式中, 为参量,对于这种势阱的处理一般要使用计算机。
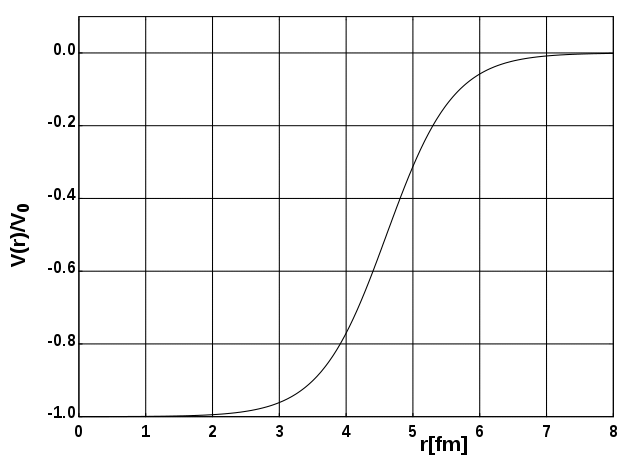
Fig:伍兹-萨克森势阱
理论计算表明,不同势阱的选择对推导得到能级的次序影响很小。我们回过头来考虑直角势阱与谐振子势阱。对于谐振子势阱,有:
其中 为 谐振子量子数, 为 径向量子数, 为 轨道量子数。
对于直角势阱有:
其中 是贝塞尔函数 的根。
对比直角势阱与谐振子势阱(包括数值计算伍兹-萨克森势阱),我们发现只能给出 ,, 三个幻数。这说明:除了势阱的形状之外,尚需考虑别的重要因素。
自旋-轨道耦合
原子核中核子的自旋-轨道耦合是很强的,实验表明,核子的自旋-轨道耦合不但存在,而且很大。在考虑自旋-轨道耦合之后,能级会发生劈裂,并且会改变能级次序。由于能级的劈裂,将会出现新的壳层。
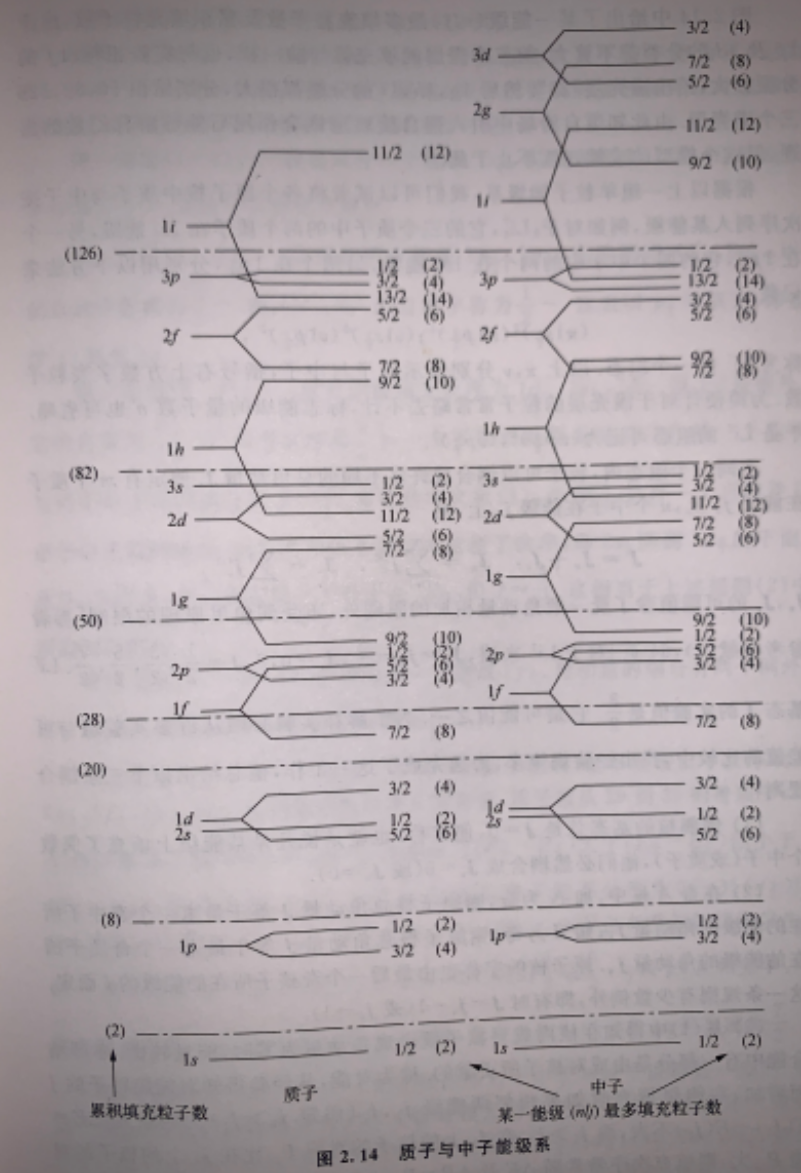
Fig:考虑自旋-轨道耦合后的核子能级
两个幻数之间的各能级组成一个 主壳层,主壳层之间的每个能级叫做 支壳层。新的主壳层的形成,是由于有些能级劈裂得特别大。
壳结构理论能够给出所有的幻数。另外,根据理论预言,在质子数为 ,中子数为 的原子核为双环核,在该核及其附近的一些核可能具有相当大的稳定性。
对关联
上面的讨论基于包括自旋-轨道耦合在内的平均场,以及核子可以独立的在平均场中运动的假设。作为壳模型的改进,我们还应该考虑核子间存在的较小的 “剩余” 相互作用,即除了平均场以外的部分。
许多实验现象表明:两个同类核子间可以存在重要的相互关联,叫做 对关联。
忽略对关联时,在费米能量 之下的每一状态都被粒子占有,在费米能量以上的态则是空缺的。考虑对关联时,理论给出,平均占有数是单粒子状态能量 的函数:
为由于相互作用产生的 能隙。在引入对关联之后,平均占有数在费米能处并不发生突变,而是在 的能量间隔内连续改变。这表示原子核的基态并不是单一的组态,而决定于许多组态的线性组合。
偶偶核的最低激发态是由核子对的崩溃产生的,结果会使核子对的一个粒子处于激发态。因此,形成了一个空穴与一个非成对粒子,通常称为准粒子。
对关联的理论比较复杂,此处不做过多展开。其在壳模型和集体模型中具有重要应用。
壳模型的应用
原子核基态的角动量和宇称
当质子和中子都填满最低的一些能级时,原子核的能量最低,称为基态。我们现在来讨论原子核处于基态时的能级特性——自旋和宇称。
对于 双幻核 ,质子数与中子数都是幻数,正好填满各自的主壳层,每一个能级的角动量为零,原子核的自旋为零,宇称为 。
对于 偶偶核,质子数与中子数都是偶数,由于对力的最用,成对的核子的角动量恰好相反。如此,这两个核子对于总角动量的贡献为零。偶偶核的自旋为零,宇称为 。
对于 奇 核来说,根据壳模型,其自旋和宇称由填充壳层的最后那个奇数的核子的状态决定。奇 核的自旋总是半整数。
对于 奇奇核 来说,其宇称和自旋由最后两个核子状态决定。
另外,壳模型对于解释同核异能素岛、 衰变、核磁矩、核电四极矩、 跃迁概率上也有应用,此处不展开说明。
集体模型
壳模型本身也存在很多缺陷,对于远离双幻核区域的磁矩、电四极矩、 跃迁概率的解释遇到了很大困难。壳模型的成功表明核中粒子的独立运动有一定意义,但是其应用范围只限于双幻核附近的球形核。
原子核的运动模式,除核内存在核子的独立运动以外,许多事实还表明原子核具有集体运动的形式。
特别明显的是偶偶核的能级规律:
- 在双幻核附近,可以用壳模型解释。称为 粒子能级
- 在离双幻核稍远的原子核 ,其低激发态能级之间的距离大致相等。这与谐振子的能级特点相符,称为 振动能级。
- 在远离双幻核的原子核 。这类能级的自旋为 ,其能量之比大致为 ,我们发现这与角动量平方的本征值特点相符,这表明这种能级应当是原子核转动形成的,称为 转动能级。
振动能级与转动能级的规律是壳模型无法解释的。我们把壳模型进行推广,在考虑核子独立运动的同时,还要考虑原子核的集体运动,由此得到 集体模型。
集体模型的基础是壳模型,它保留了壳模型的基本概念,即认为核子在平均核场中独立运动并形成壳层结构。但它对壳模型作了重要补充,认为原子核可以发生形变(指球形变为非球形),并产生转动和振动等集体运动。
原子核的平衡形状依赖于以下两种作用相互竞争的结果:
- 外围核子对核心的极化作用
- 核心保持球形的作用
原子核的转动是指原子核势场空间取向的变化。对于球形核,它的势场是球对称的,没有特定的方向,所以球形核无集体转动可言的。同理,形状为轴对称的原子核绕对称轴的集体转动也是没有意义的。
原子核的振动是指原子核在平衡形状附近作振荡。假定核物质是不可压缩的,则在振动过程中核的体积保持不变,因而原子核的振动一般都是体积不变而形状变化的表面振动。
原子核集体运动的周期一般要比核内单个核子运动的周期长得多;换句话说,单粒子运动要比集体运动快得多。这种近似地把单粒子运动和集体运动分开考虑的方法,叫做 绝热近似。
转动能级和振动能级
转动能级
假定形变原子核的平衡形状是一个旋转椭球,对称轴为 ,那么只有绕垂直于 轴的转动才是有意义的。考虑角动量 垂直于 。此时形变核的势场将不是球对称的,核子在 轴对称的椭球势场 中运动时,核子的角动量 不是守恒量,只有在 轴的投影 才是守恒量。考虑转动时,体系的总角动量可以写为:
描述轴对称原子核的转动时,可以用三个量子数表示:
- 总角动量量子数
- 在对称轴 上的投影
- 在 轴上的投影
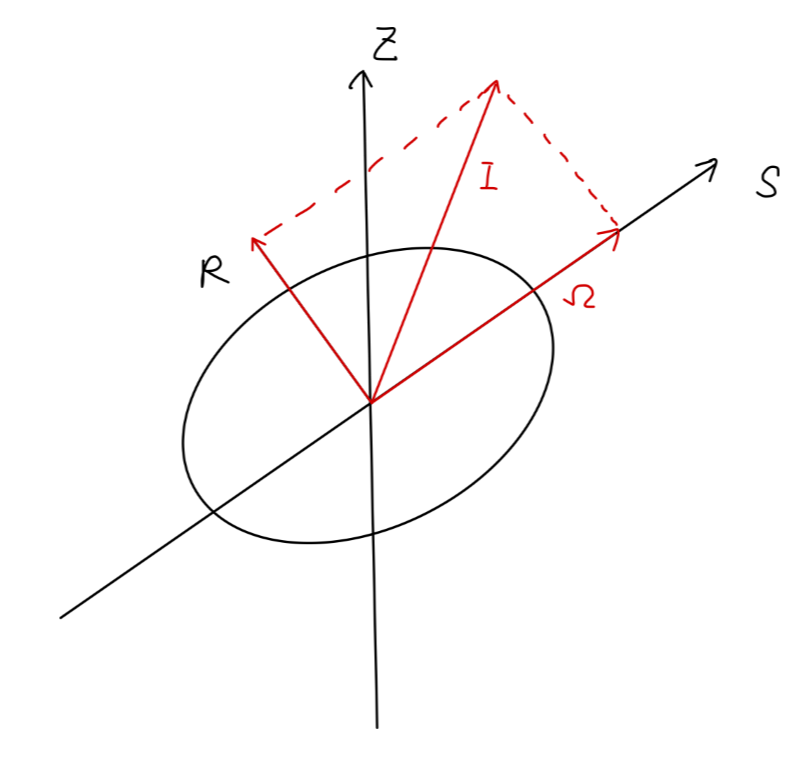
Fig:形变核的矢量模型
对于偶偶核来说,其能级公式最简单:
其中 为转动惯量。
偶偶核
可以证明,偶偶核的自旋只能取偶数、宇称为正。所以 取值为:
对于形变的奇 核,此处不过多展开。
振动能级
先简单介绍一下原子核的定量描述。假定核物质是不可压缩的,在形变中体积保持不变是,任何形变的原子核的表面在球坐标中的表示式 可以用球谐函数表示为:
代表质心的移动; 代表四极形变; 代表八极形变。研究表明, 的形变最重要; 的形变只有在重核中才重要。
当慢壳层外的核子数不多时,原子核的稳定形变还不能发生。它的平衡形状仍然是球形,这种原子核,主要出现在 和 ,这个区域通常称为过渡区,过渡区的原子核具有明显的振动运动,这种振动主要为在球形附近作 四极振动。
对于偶偶核来说,其振动能量为:
这种模式的元激发称为声子。 对应于声子数。每个声子带两个角动量,宇称总为正。
第一激发态的能级特性为 。第二激发态为 。
参考资料
- 原子核物理 卢希庭
- By !Original: ChzzVector: Benjamin Bannier - http://skipper.physics.sunysb.edu/~benjamin/ws/, Public Domain, https://commons.wikimedia.org/w/index.php?curid=14388772
- http://jpk.pku.edu.cn/course/hwl/script/chap_8_4-6.pdf
- 封面图 by 由英语维基百科的Bakken,CC BY-SA 3.0,https://commons.wikimedia.org/w/index.php?curid=15039395










