前言：上一篇在矢量力学的框架下介绍了运动学的基本内容。通过引入参考系，我们能够对质点运动的位矢、速度、加速度等物理量进行描述。在考虑到不同的参考系之间的变换之后，可以得到对应的运动量的变换关系。在接下来的牛顿力学部分，我们介绍力与运动的关系。

牛顿运动定律

牛顿运动定律是牛顿力学的基础。

牛顿运动定律（Newton’s laws of motion）描述施加于物体的外力与物体所呈现出的运动彼此之间的关系。这定律被誉为经典力学的基础，牛顿运动定律的现代版本通常表述为[1][2]^{[1][2]}：

  • 第一定律：假若施加于某物体的外力为零，则该物体的运动速度不变（惯性定律）
  • 第二定律：施加于物体的外力等于此物体的质量与加速度的乘积（加速度定律）
  • 第三定律：当两个物体相互作用于对方时，彼此施加于对方的力，其大小相等、方向相反（作用力与反作用力定律）

在中学和普通物理的学习中对牛顿定律已经了解很多了，现在再说明几个问题：

1. 牛顿定律可以被证明吗？
所有的定律都是无法被证明的。定律是通过大量具体的客观事实归纳而成的结论。在牛顿定律的基础上，我们计算的结果如果符合实验，我们就有理由相信这个基础是可靠的，尽管如此，也不能说明牛顿定律在任何场景是正确的（事实上，牛顿定律确实有本身的局限性）。在牛顿的经典力学中，我们从牛顿定律出发，逐步推导出矢量力学体系。

2. 牛顿第一定律的意义
牛顿第一定律在物理学中具有重要意义，因为牛顿第一定律与 惯性系 密切相关。对于牛顿第一定律与惯性系的关系，有一些不同的观点：

  • 牛顿绘景[3]^{[3]}
    牛顿认为，第一定律是物理定律，因此具有可证伪性，即做实验可以核对第一定律是否正确。在做这实验时，必须测量物体的运动速度，但这涉及到参考系的设定。因此，可以更详细地将第一定律表明为[4]^{[4]}：

    采用某种参考系来做测量，假若施加于一个物体的外力为零，则该物体的运动速度不变。

    尽管在《自然哲学的数学原理》里没有明确地指明应该怎样诠释作用力，从第一定律的内容可以推论，牛顿认为，零作用力案例可以很容易地被辨认出来。这案例能够对于惯性参考系给出定义：假若，从一个参考系观测，不受力的物体的运动速度不变，则这参考系是惯性参考系。在宇宙中，存在着无数可能的参考系，在这些参考系中，满足第一定律的参考系称为“惯性参考系”，而其它不满足第一定律的参考系称为“非惯性参考系”。因此，第一定律可以被视为惯性参考系的定义。从做实验观察物体的运动行为，就可以辨别出哪个是惯性参考系，哪个不是惯性参考系[5]^{[5]}。
    在做实验核对第一定律时，还必须测量是否有外力施加于物体，这意味着必须对于力给出严格定义。但是他并没有对于力给出严格定义。

  • 基尔霍夫绘景[3]^{[3]}
    另外还有一种常见的绘景是由古斯塔夫·基尔霍夫最先给出，后来又获得恩斯特·马赫、海因里希·赫兹等人的支持。按照这种绘景，第一定律被视为第二定律的零外力特别案例，而第二定律则被视为力的定义，即将力定义为质量与加速度的乘积。这样，就不必涉及引入力的概念这棘手的任务。假若采用这种绘景，则第二定律不再拥有任何物理内涵，[6]^{[6]}而牛顿并没有发现力是质量与加速度的乘积，因为这只是一个定义，牛顿发现的是，物理定律比较容易用力的概念来表达。

    这种绘景会导致的后果是，整个经典力学会变成一种公理化理论，所有结论都是源自于这个定义，而不是源自于更为物理学者青睐的从做实验总结出的“自然定律”。只有从某种特定的参考系观测，才可以将牛顿定律与实际物理接轨，这种特定的参考系就是惯性参考系，通过做实验可以找到无限数量的这种惯性参考系。从任何其它种参考系观测，都无法达成接轨的目标。更具体而言，只有从惯性参考系才可观测到不受力物体的运动速度不变。[6]^{[6]}

另外爱因斯坦的等效原理对惯性系也做出了一些诠释，在这里不展开了。牛顿绘景比较符合物理直觉，但是不由得陷入力与惯性系循环定义的陷阱中，基尔霍夫绘景回避了这个问题。总之，我们如果不深究其中的哲学内核，完全可以简单的承认牛顿定律，认为惯性系就是牛顿定律成立的参考系，然后继续开始理论推导。

3. 牛顿定律的局限性

  1. 高速
    在粒子速度接近光速时，牛顿定律失效。我们需要使用相对论对粒子进行描述。
  2. 小尺度
    不确定关系使得经典力学中确定的轨道变得没有意义，量子力学取代经典力学。
  3. 混沌
    大量粒子组成的体系中，虽然原则上利用牛顿定律是以求出每个粒子确定的轨道。但在事实上是不可解的。

伽利略相对性原理

伽利略最早提出 伽利略相对性原理：物理定律在一切惯性参考系中具有相同的形式，任何力学实验都不能区分静止和匀速运动的惯性参考系。

伽利略相对性原理实际上将一系列相对作匀速运动的惯性参考系等同起来，构成一个等价类。联系起这些互相等价的参考系之间的变换就是 伽利略变换。

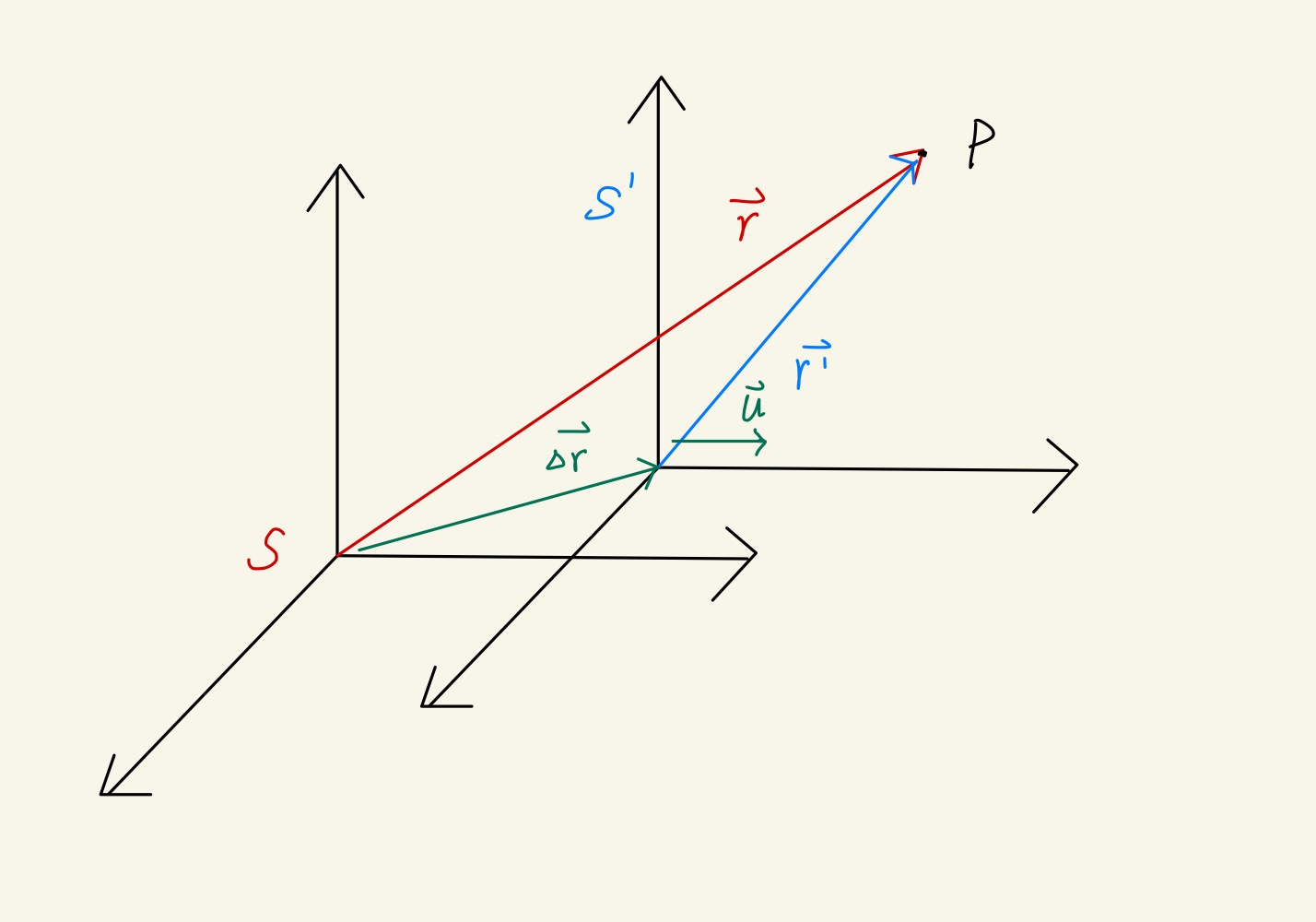
考虑 位矢、速度 的伽利略变换：

{r′=r−Δrv′=v−Δv\left\{\begin{aligned} &\bm{r'}=\bm{r}-\bm{\Delta r}\\ &\bm{v'}=\bm{v}-\bm{\Delta v}\\ \end{aligned}\right.

其中 Δr,Δv\bm{\Delta r},\bm{\Delta v} 表示相对位矢和相对速度。而加速度在伽利略变换下是不变的。

质点动力学

动力学主要研究作用于物体的力与物体运动的关系。动力学的研究对象是运动速度远小于光速的宏观物体。在以下我们先讨论在惯性系中的质点动力学，然后再推广到非惯性系中去。

惯性系

在惯性系中，牛顿第二定律给出了运动与力的关系：

此处我们采用牛顿绘景，认为力是改变物体运动状态的原因。

F=ma(1)\bm{F} = m\bm{a} \tag{1}

非惯性系

在非惯性系中，牛顿运动定律不成立。但是我们可以通过坐标变换将非惯性系与惯性系联系起来，从而给出在非惯性系中力与运动的关系。

对应上一篇中提到的一般参考系之间的加速度的变换，我们可以做出如下推导：
假设 SS 为一个惯性参考系，S′S' 是相对 SS 做 ω(t)\bm{\omega}(t) 的角运动，Δr(t)\Delta r(t) 平动的非惯性参考系。

对于一个质点，在惯性参考系 SS 中，由牛顿第二定律，有：

FS=maS\bm{F}_S = m\bm{a}_S

坐标变换给出：

aS=aS′′+2ω×v′S′+β×r′S′+ω×(ω×r′S′)+ΔaS\bm{a_{S}}=\bm{a}'_{S'}+2\bm{\omega}\times\bm{v'}_{S'}+\bm{\beta}\times\bm{r'}_{S'}+\bm{\omega}\times(\bm{\omega}\times\bm{r'}_{S'})+\Delta\bm{a}_S

由此可得：

aS=aS′′+aS′′\bm{a}_S=\bm{a} _ {S'}'+\bm{a}''_{S}

其中，我们用 aS′′\bm{a}''_{S} 表示参考系所带来的牵连加速度。

由此，在 SS 系中写出动力学方程：

FS=maS=maS′′+maS′′\begin{aligned} \bm{F}_S &= m\bm{a}_S\\ &=m\bm{a _ {S'}'}+m\bm{a}''_{S} \end{aligned}

在经典力学中，力是不随参考系变化的，于是：

FS′=FS\bm{F}_{S'} = \bm{F}_{S}

得到：

FS′=maS′′+maS′′\bm{F}_{S'} =m\bm{a }_ {S'}'+m\bm{a}''_{S}

我们发现在引入 惯性力

FS′′′=−maS′′(2)\bm{F}''_{S'}=-m\bm{a}''_{S} \tag{2}

后，牛顿第二定律在 非惯性系 S′S' 中也成立：

∑FS′=FS′+FS′′′=maS′′(3)\sum \bm{F}_{S'}=\bm{F}_{S'}+\bm{F}^{''}_{S'}=m\bm{a}'_{S'} \tag{3}

因此可以说，在经典力学中，只要引入惯性力，那么对惯性系使用的任何方法都可以应用到非惯性系中去。

参考系变换所引起的向心加速度，科里奥利加速度所对应的惯性力分别称作 离心力，科里奥利力。

地球自转偏向力就是把地球看做一个惯性系所引入的科里奥利力。

质点运动定理

从质点运动方程出发，可以从其他观点来看质点的运动：

  1. 动量定理
    牛顿第二定律

mr¨=Fm\ddot{\bm{r}}=\bm{F}

两边同时对时间积分，得到：

mr˙∣t1t2=∫t1t2Fdt(4)m\dot{\bm{r}}|_{t_1}^{t_2}=\int_{t_1}^{t_2}\bm{F}dt\tag{4}

定义 动量 p\bm{p} 为质量与速度的乘积：

p=mv(5)\bm{p}=m\bm{v} \tag{5}

等式右边的积分项称作力 F\bm{F} 在 t1t_1 到 t2t_2 时间内的 冲量。因此从 (4)(4) 式可以得到 动量定理 ：一段时间内动量的变化等于外力的冲量。

p2−p1=I\bm{p}_2-\bm{p}_1=\bm{I}

在引入动量之后，力又可以写做：

F=dpdt\bm{F}=\frac{d\bm{p}}{dt}

这是一个很重要的式子。

  1. 角动量定理
    由牛顿第二定律可得

mr×r¨=r×F\bm{m}\bm{r}\times\ddot{\bm{r}}=\bm{r}\times\bm{F}

考虑到：

ddt(r×r˙)=r˙×r˙+r×r¨=r×r¨\begin{aligned} \frac{d}{dt}(\bm{r}\times\dot{\bm{r}})&=\dot{\bm{r}}\times\dot{\bm{r}}+\bm{r}\times\ddot{\bm{r}}\\ &=\bm{r}\times\ddot{\bm{r}}\\ \end{aligned}

两边同时对时间积分后，得到：

mr×r˙∣t1t2=∫t1t2r×Fdt(6)m\bm{r}\times\dot{\bm{r}}|_{t_1}^{t_2}=\int_{t_1}^{t_2}\bm{r}\times\bm{F}dt\tag{6}

引入 角动量 L\bm{L}：

L=r×p=mr×r˙(7)\bm{L}=\bm{r}\times\bm{p}=m\bm{r}\times\dot{\bm{r}}\tag{7}

以及 冲量矩 J\bm{J}：

J=∫t1t2Mdt=∫t1t2r×Fdt(8)\bm{J}=\int_{t_1}^{t_2}\bm{M}dt=\int_{t_1}^{t_2}\bm{r}\times\bm{F}dt\tag{8}

结合 (6)(6)，得到 角动量定理 ：一段时间内角动量的变化等于外力矩的冲量矩：

L2−L1=J(9)\bm{L}_2 - \bm{L}_1 = \bm{J} \tag{9}

在引入角动量后，力矩又可以写为：

M=dLdt(10)\bm{M} = \frac{d\bm{L}}{dt} \tag{10}

  1. 动能定理
    由质点运动方程可得

mr˙⋅r¨=r˙⋅F\bm{m}\dot{\bm{r}}\cdot\ddot{\bm{r}}=\dot{\bm{r}}\cdot\bm{F}

考虑到：

ddt(12r˙2)=r˙⋅r¨\frac{d}{dt}(\frac{1}{2}\dot{\bm{r}}^2)=\dot{\bm{r}}\cdot\ddot{\bm{r}}

对两边同时积分可得：

12mr˙2∣t1t2=∫12F⋅dr(12)\frac{1}{2}m\dot{\bm{r}}^2|_{t_1}^{t_2} = \int_{1}^{2} \bm{F}\cdot\bm{dr}\tag{12}

上式左边为质点 动能 EkE_k 的变化，右边为外力所做的功 WW。从 (12)(12) 式得到 动能定理：一段时间内动能的变化等于外力所做的功：

E2−E1=W(13)E_2 - E_1 = W \tag{13}

虽然从上面的推导来看，似乎 动量定理、角动量定理、动能定理 是从牛顿运动定律推导而来的。但事实上，这些运动定理比牛顿运动定律更为普适。因为在量子力学中：动量、角动量、能量比力更为基本。

质点组动力学

当研究的体系不止超过一个质点时，我们需要列出所有质点的运动方程。对于一个两体系统来说，这个方程是容易求解的。但是对于三个质点以及以上的系统，求出解析解的过程很复杂，或者解析解根本不存在。但是，我们可以对整个系统的动力学性质作一些讨论。

两体问题

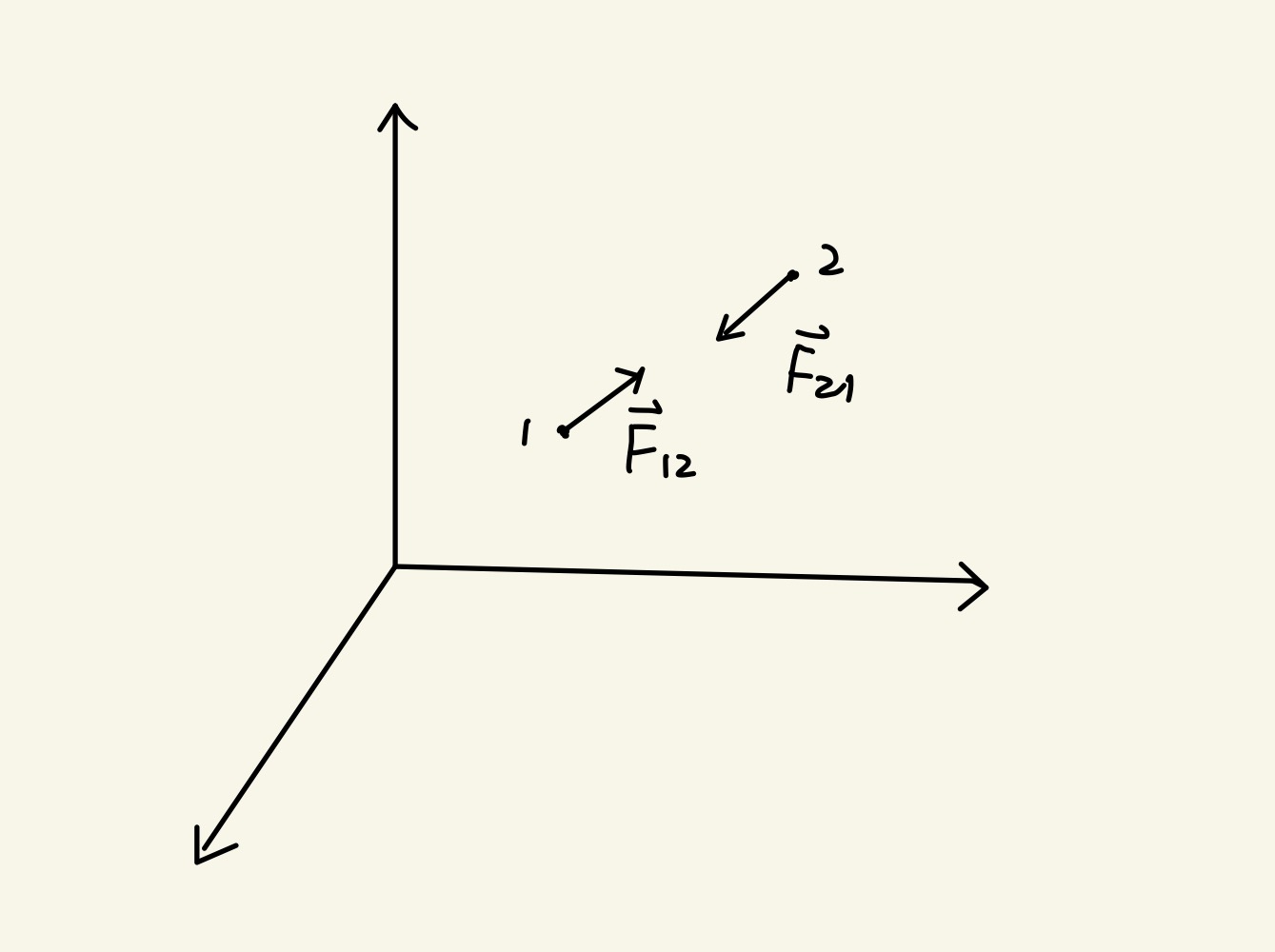
质点组动力学有一类特殊问题——两体问题：指两质点彼此相互作用，但不受到其他力的作用。动力学方程写做：

{m1r¨1=F12m2r¨2=F21\left\{\begin{aligned} & m_1\ddot{\bm{r}}_1=\bm{F}_{12}\\ & m_2\ddot{\bm{r}}_2=\bm{F}_{21}\\ \end{aligned}\right.

其中 F12\bm{F}_{12} 表示质点 11 受到质点 22 的作用力。
由牛顿第三定律可得：

F12=−F21\bm{F}_{12}=-\bm{F}_{21}

引入 质心位矢：

R=m1r1+m2r2m1+m2\bm{R} = \frac{m_1\bm{r}_1+m_2\bm{r}_2}{m_1+m_2}

相对位矢：

r=r2−r1\bm{r} = \bm{r}_2-\bm{r}_1

于是运动方程可以重写为：

{R¨=0μr¨=F21(14)\left\{\begin{aligned} & \ddot{\bm{R}}=0\\ & \mu \ddot{\bm{r}}=\bm{F}_{21}\\ \end{aligned}\right.\tag{14}

其中

μ=m1m2m1+m2(15)\mu=\frac{m_1m_2}{m_1+m_2}\tag{15}

为 约化质量。

质点组运动定理

考虑一个质点组的运动，对于质点 ii 来说，受到质点 jj 的作用力 Fij\bm{F}_{ij} 以及外部作用力 Fi\bm{F}_i 有：

mir¨i=∑j≠iFij+Fi(16)m_i\ddot{\bm{r}}_i=\sum_{j\neq i}\bm{F}_{ij}+\bm{F}_i\tag{16}

求解出每个质点的运动是很麻烦的。在二体运动中我们将两个运动方程相加后，利用牛顿第三定律消去内部作用力，由此得到了质心的运动方程。这启发我们，消去内部作用力去得到一些质点组的整体性质。

质点系动量定理

∑imir¨i=∑i(∑j≠iFij+Fi)=∑i∑j≠iFij+∑iFi=12∑ij,i≠j(Fij+Fji)+∑iFi=∑iFi\begin{aligned} \sum_{i}m_i\ddot{\bm{r}}_i&=\sum_{i}(\sum_{j\neq i}\bm{F}_{ij}+\bm{F}_i)\\ &=\sum_{i}\sum_{j\neq i}\bm{F}_{ij}+\sum_{i}\bm{F}_i\\ &=\frac{1}{2}\sum_{ij,i\neq j}(\bm{F}_{ij}+\bm{F}_{ji})+\sum_{i}\bm{F}_i\\ &=\sum_{i}\bm{F}_i \end{aligned}

上式中的求和符号 ∑ij,i≠j\sum_{ij,i\neq j} 表示对每一对不相等的 i,ji,j 求和。这样算每一个力算了两次，因此前面要乘以 12\frac{1}{2}。

两边对时间积分得到：

ΔPtotal=Itotal(17)\Delta\bm{P}_{total}=\bm{I}_{total}\tag{17}

即 质点系动量定理：一个质点系总动量的变化等于外力的总冲量

质点系角动量定理

∑imiri×r¨i=∑i(∑j≠iri×Fij+ri×Fi)=∑i∑j≠iri×Fij+∑iri×Fi=12∑ij,i≠j(ri×Fij+rj×Fji)+∑iri×Fi=12∑ij,i≠j(rij×Fji)+∑iri×Fi=∑ir˙ij⋅Fi\begin{aligned} \sum_{i}m_i\bm{r}_i\times\ddot{\bm{r}}_i&=\sum_{i}(\sum_{j\neq i}\bm{r}_i\times\bm{F}_{ij}+\bm{r}_i\times\bm{F}_i)\\ &=\sum_{i}\sum_{j\neq i}\bm{r}_i\times\bm{F}_{ij}+\sum_{i}\bm{r}_i\times\bm{F}_i\\ &=\frac{1}{2}\sum_{ij,i\neq j}(\bm{r}_i\times\bm{F}_{ij}+\bm{r}_j\times\bm{F}_{ji})+\sum_{i}\bm{r}_i\times\bm{F}_i\\ &=\frac{1}{2}\sum_{ij,i\neq j}(\bm{r}_{ij}\times\bm{F}_{ji})+\sum_{i}\bm{r}_i\times\bm{F}_i\\ &=\sum_{i}\dot{\bm{r}}_{ij}\cdot\bm{F}_i\\ \end{aligned}

两边对时间积分得到：

Ltotal=Jtotal(18)\bm{L}_{total}=\bm{J}_{total}\tag{18}

即 质点系动量定理：一个质点系总角动量的变化等于外力矩的总冲量矩

质点系动能定理

∑imir˙i⋅r¨i=∑i(∑j≠ir˙i⋅Fij+r˙i⋅Fi)=∑i∑j≠ir˙i⋅Fij+∑ir˙i⋅Fi=12∑ij,i≠j(r˙i⋅Fij+r˙i⋅Fji)+∑ir˙i⋅Fi=12∑ij,i≠j(r˙ij⋅Fji)+∑ir˙i⋅Fi\begin{aligned} \sum_{i}m_i\dot{\bm{r}}_i\cdot\ddot{\bm{r}}_i&=\sum_{i}(\sum_{j\neq i}\dot{\bm{r}}_i\cdot\bm{F}_{ij}+\dot{\bm{r}}_i\cdot\bm{F}_i)\\ &=\sum_{i}\sum_{j\neq i}\dot{\bm{r}}_i\cdot\bm{F}_{ij}+\sum_{i}\dot{\bm{r}}_i\cdot\bm{F}_i\\ &=\frac{1}{2}\sum_{ij,i\neq j}(\dot{\bm{r}}_i\cdot\bm{F}_{ij}+\dot{\bm{r}}_i\cdot\bm{F}_{ji})+\sum_{i}\dot{\bm{r}}_i\cdot\bm{F}_i\\ &=\frac{1}{2}\sum_{ij,i\neq j}(\dot{\bm{r}}_{ij}\cdot\bm{F}_{ji})+\sum_{i}\dot{\bm{r}}_i\cdot\bm{F}_i\\ \end{aligned}

两边对时间积分得到：

∑iEki=Wint+Wext(19)\sum_{i}E_{ki}=W_{int}+W_{ext}\tag{19}

即 质点系动量定理：一个质点系总动能的变化等于内力做功和外力做功之和。

质心系

在两体问题中，我们采用质心位矢与相对位矢改写运动方程，我们发现这样效果很好，得到的运动方程形式很简单。这些提示我们，可以将质点系的整体运动与相对运动区分开来。

首先引入质心位矢（各个质点位矢以质量为权重加权平均）：

R=∑imiri∑imi\bm{R}=\frac{\sum_{i}m_i\bm{r}_ i}{\sum_{i}m_i}

对于连续体来说，质心位矢为：

rc=∫rρ(r)dr∫ρ(r)dr\bm{r}_c = \frac{\int \bm{r}\rho(\bm{r})d\bm{r}}{\int\rho(\bm{r})d\bm{r}}

由此将各个质点的运动方程直接相加，就可以得到质心的运动方程：

MR¨=FtotalM\ddot{\bm{R}}=\bm{F}_{total}

上式中 M=∑imiM = \sum_{i}m_i 为系统中所有质点的总质量。

如何剔除整体运动的部分，一个很自然的想法是在质心参考系（简称质心系 ）中求解问题。注意，质心系是一个平动系，不一定是惯性系。

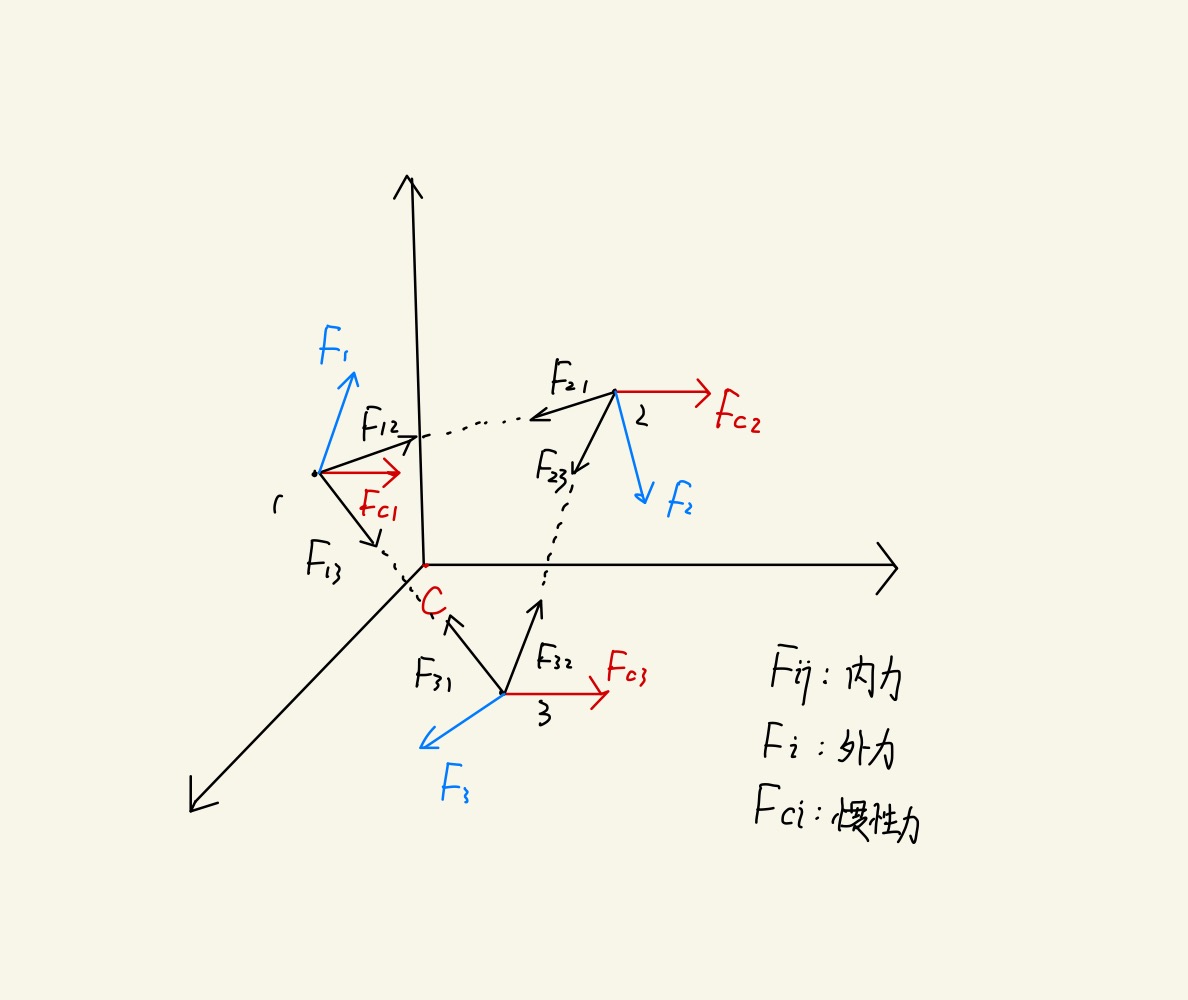
设质心的加速度为 ac\bm{a}_c，因此质心系中的每一个质点都要受到一个惯性力 Fc=−mac\bm{F}_c = -m \bm{a}_c 的作用。

我们可以分别考虑惯性力的冲量、冲量矩、做功情况。

质心系中惯性力的冲量

I=∫∑iFcidt=−∫∑imiacdt=−∫Ftotaldt=−Itotal\begin{aligned} \bm{I}&=\int \sum_{i} \bm{F}_{ci}dt\\ &=-\int \sum_{i} m_{i}\bm{a}_{c}dt\\ &=-\int \bm{F}_{total}dt\\ &=-\bm{I}_{total}\\ \end{aligned}

我们发现惯性力的冲量与合外力的冲量正好抵消。因此，在质心系中，动量守恒。

同理也可得到惯性力矩的冲量矩与合外力矩的冲量矩也相互抵消。因此，在质心系中，角动量守恒。

考虑惯性力做功：

W=∫∑iFi⋅dri=−∫∑imiac⋅dri=−∫ac⋅∑imidri=−∫ac⋅(∑imi)drc=0\begin{aligned} W&=\int\sum_{i}\bm{F}_i\cdot\bm{dr}_i\\ &=-\int\sum_{i}m_i\bm{a}_c\cdot\bm{dr}_i\\ &=-\int\bm{a}_c\cdot \sum_{i}m_i\bm{dr}_i\\ &=-\int\bm{a}_c\cdot (\sum_{i}m_i)\bm{dr}_c\\ & = 0 \end{aligned}

最后一步是因为在质心系中，质心位矢的变化显然为零。

可得，在质心系中，惯性力做功为零。

根据以上讨论，我们发现质心系具有很好的性质，在实际问题中，我们也时常在质心系中讨论问题，这是很方便的。

参考资料

  1. Halliday, David; Resnick, Robert; Walker, Jerl, Fundamental of Physics 7th, USA: John Wiley and Sons, Inc., 2005, ISBN 0-471-23231-9,第88f页
  2. Young, Hughy; Freedman, Roger; Ford, A., Sears and Zemansky’s University Physics with Modern Physics 13, Addison-Wesley, 2011, ISBN 978-0321696861,第104页
  3. 维基百科编者. 牛顿第一运动定律[G/OL]. 维基百科, 202020201220. https://zh.wikipedia.org/w/index.php?title=牛顿第一运动定律&oldid=63329445.
  4. French, Anthony, Newtonian Mechanics, 1971，第162-163页
  5. O’Sullivan, Colm, Newton’s Laws of Motion: Some interpretations of the formalism, American Journal of Physics, 1980, 48 (2): 131–133, doi:10.1119/1.12186
  6. 麦克斯韦, 詹姆斯, Matter and Motion, D.Van Nostrand, 1878，第27页
  7. 梁昆淼,力学,下册,第四版,第24页