量子场论笔记（十七）：电子顶点函数

电子顶点函数

形状因子

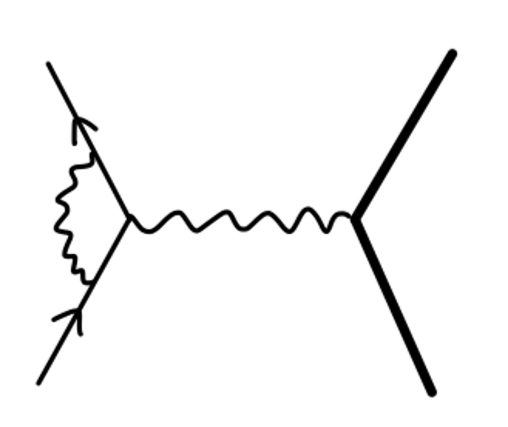
现在我们来讨论顶点修正。一阶修正为：添加一个额外的虚光子连接两条腿，构成一个圈。

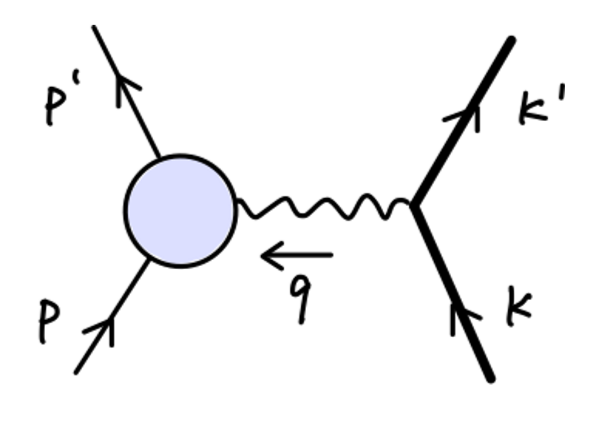
一般情况，我们用下图表示所有的 amputated 圈图的总和。

令它对应的取值为：$-ie\Gamma^{\mu}(p',p)$，跃迁矩阵元可以写为：

$i\mathcal{M}= ie^2(\bar{u}(p')\Gamma(p',p)u(p))\frac{1}{q^2}(\bar{u}(k')\gamma_{\mu}u(k))\tag{1}$

更一般的讨论，$\Gamma^{\mu}$ 是对顶点的修正，也出现在其他的过程中。以下哈密顿量描述了电子与电磁场的相互作用：

$\Delta H_{int} = \int d^3x eA_{\mu}^{cl} j^{\mu}$

其中 $j^{\mu} = \bar{\psi}(x)\gamma^{\mu}\psi(x)$，$A^{cl}_{\mu}$ 为一个固定的经典势。根据微扰论，散射矩阵元为：

$i\mathcal{M}(2\pi)\delta(p'^0-p^0) = -ie\bar{u}(p')\gamma^{\mu}u(p)\cdot\tilde{A}^{cl}_{\mu}(p'-p)$

当考虑顶点修正的情况，需要将散射矩阵元的表达式修改为：

$i\mathcal{M}(2\pi)\delta(p^0-p) = -ie\bar{u}(p')\Gamma^{\mu}(p',p)u(p)\cdot\tilde{A}^{cl}_{\mu}(p'-p)$

$\Gamma^{\mu}(p',p)$ 应当是一个 $p,p',\gamma^{\mu},m,e,\cdots$ 构成的函数。其领头阶来自于树图的贡献：

$\Gamma^{\mu} = \gamma^{\mu}$

我们考虑次领头阶的贡献，$\Gamma^{\mu}$ 矩阵可以写为：

$\Gamma^{\mu} = \gamma^{\mu}\cdot A + (p'^{\mu}+p^{\mu})\cdot B + (p'^{\mu}-p^{\mu})\cdot C \tag{2}$

现在考虑 $A,B,C$ 可能具有的形式。若含有 $\cancel{p}$ 或 $\cancel{p}'$，可以化简为：

$\begin{aligned} \cancel{p} u(p) = m\cdot u(p)\\ \bar{u}(p') \cancel{p}'= \bar{u}(p')\cdot m \\ \end{aligned}$

那么实际上含有 $\cancel{p}$ 或 $\cancel{p}'$ 就等价于一些常数。那么唯一可能出现的非平凡的标量为：

$q^2 = -2p'\cdot p + 2m^2$

Ward 等式要求 $q_{\mu}\Gamma^{\mu} = 0$，根据 $(2)$ 式，必须要求 $C = 0$。

利用 Gordon 等式：

$\bar{u}(p')\gamma^{\mu}u(p) = \bar{u}(p')(\frac{p'^{\mu}+p^{\mu}}{2m} + \frac{i\sigma^{\mu\nu}q_{\nu}}{2m})u(p) \tag{3}$

可以将 $(2)$ 式改写为：

$\begin{aligned} \Gamma^{\mu} = \gamma^{\mu} F_1(q^2) + \frac{i\sigma^{\mu\nu}q_{\nu}}{2m}F_2(q^2) \end{aligned}$

其中 $F_1(q^2),F_2(q^2)$ 称为 形状因子 form factor。$F_1$ 称为 Dirac 形状因子，$F_2$ 称为 Pauli 形状因子。

---

我们首先对静电场中的非相对论散射进行计算。取 $A_{\mu}^{cl}(x) = (\phi(\bm{x}),\bm{0})$，得到：

$\tilde{A}^{cl}_{\mu}(q) = ((2\pi)\delta(q^0)\tilde{\phi}(\bm{q}),\bm{0})$

得到跃迁矩阵元为：

$i\mathcal{M} = -ie\bar{u}(p')\Gamma^0(p',p)u(p)\tilde{\phi}(\bm{q})$

我们假设静电场变换的很缓慢，如此 $\phi(\bm{q})$ 主要集中在 $\bm{q} = 0$ 处。我们取极限 $\bm{q}\rightarrow 0$。此时 $F_1(q^2)$ 项对散射具有主要贡献，且有：

$\bar{u}(p')\gamma^0 u(p) = u^\dagger(p')u(p) = 2E_p\xi^\dagger\xi \approx 2m\xi^\dagger\xi$

将跃迁矩阵元写为：

$i\mathcal{M} = -ie F_1(0)\tilde{\phi}(\bm{q})\cdot 2m\xi^\dagger\xi$

根据 Born 近似，这相当于是在一个势为 $V(\bm{x}) = eF_1(0)\phi(\bm{x})$ 的场中的散射。

---

类似的，我们可以计算电子在磁场中的散射。

此时四维矢势取为 $A_{\mu}^{cl}(x) = (0,\bm{A}^{cl}(\bm{x}))$，跃迁矩阵元成为：

$i\mathcal{M} = ie(\bar{u}(p')(\gamma^iF_1 + \frac{i\sigma^{i\nu}q_\nu}{2m}F_2)u(p))\tilde{A}^i_{cl}(\bm{q})$

做近似：

$u(p) = \begin{pmatrix} \sqrt{p\cdot \sigma}\xi\\ \sqrt{p\cdot \bar{\sigma}}\xi\\ \end{pmatrix} \approx \sqrt{m} \begin{pmatrix} (1-\bm{p}\cdot\bm{\sigma}/2m)\xi\\ (1+\bm{p}\cdot\bm{\sigma}/2m)\xi\\ \end{pmatrix}$

得到 $F_1$ 项可以写为：

$\begin{aligned} \bar{u}(p')\gamma^iu(p) &= 2m\xi'^\dagger(\frac{\bm{p}'\cdot\bm{\sigma}}{2m}\sigma^i+\sigma^i\frac{\bm{p}\cdot\bm{\sigma}}{2m})\xi\\ &= 2m\xi'^\dagger(-\frac{i}{2m}\epsilon^{ijk}q^j\sigma^k)\xi\\ \end{aligned}$

考虑到 $F_2$ 项前的因子实际上可以写为：

$\bar{u}(p')\frac{i\sigma^{i\nu}q_\nu}{2m}u(p) = 2m\xi'^\dagger(-\frac{i}{2m}\epsilon^{ijk}q^j\sigma^k)\xi$

可得：

$\begin{aligned} i\mathcal{M} &= ie(\bar{u}(p')(\gamma^iF_1 + \frac{i\sigma^{i\nu}q_\nu}{2m}F_2)u(p))\tilde{A}^i_{cl}(\bm{q})\\ & \underset{q\rightarrow 0}{\approx} i(2m)e(\xi'^\dagger(-\frac{i}{2m}\epsilon^{ijk}q^j\sigma^k)(F_1(0)+F_2(0))\xi)\tilde{A}^i_{cl}(\bm{q})\\ &=-i(2m)e(\xi'^\dagger\frac{-1}{2m}\sigma^k(F_1(0)+F_2(0))\xi)\tilde{B}^k(\bm{q})\\ \end{aligned}$

其中用到了傅里叶变换之后的磁场与矢势的关系：

$\tilde{B}^k(\bm{q}) = -i\epsilon^{ijk}q^i\tilde{A}_{cl}^j(\bm{q})$

利用 Born 近似，可以写出对应的散射势：

$\begin{aligned} &V(\bm{x}) = -\langle \bm{\mu} \rangle \cdot \bm{B}(\bm{x})\\ &\langle\bm{\mu}\rangle = \frac{e}{m}[F_1(0) + F_2(0)]\xi'^\dagger\frac{\bm{\sigma}}{2}\xi \end{aligned}$

利用电子磁矩的表达式：

$\bm{\mu} = g(\frac{e}{2m})\bm{S}$

得到 Lande g-factor 为：

$g = 2[F_1(0) + F_2(0)] = 2 +\mathcal{O}(\alpha)$

一阶圈图的计算

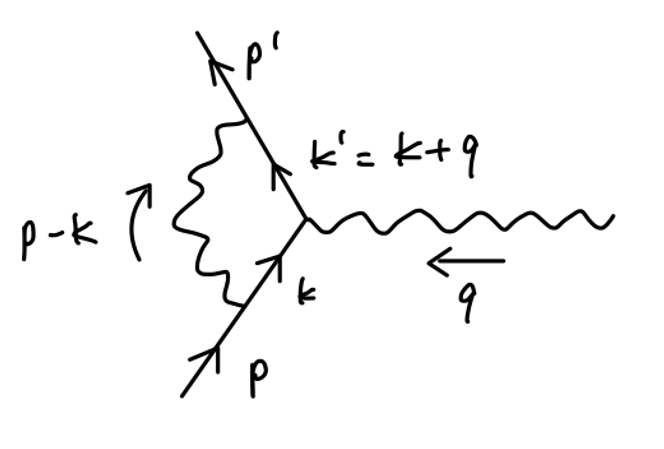
现在考虑一阶圈图的贡献:

$\begin{aligned} &\bar{u}(p')\delta\Gamma^{\mu}(p',p)u(p)\\ &= \int \frac{d^4k}{(2\pi)^4}\frac{-ig_{\nu\rho}}{(k-p)^2+i\epsilon}\bar{u}(p')(-ie\gamma^{\nu})\frac{i(\gamma\cdot k' +m)}{k'^2-m^2+i\epsilon} \gamma^{\mu} \frac{i(\gamma\cdot k +m)}{k^2-m^2+i\epsilon}(-ie\gamma^{\rho})u(p)\\ &= 2ie^2 \int \frac{d^4k}{(2\pi)^4} \frac{\bar{u}(p')(\gamma\cdot k\gamma^{\mu}\gamma\cdot k' + m^2 \gamma^{\mu} - 2m(k+k')^{\mu})u(p)}{((k-p)^2 + i\epsilon)(k'^2 -m^2 + i\epsilon)(k^2 -m^2 + i\epsilon)} \end{aligned}\tag{4}$

---

我们现在的任务成为了：对上述积分的计算。为了达成这一目的，我们接下来介绍 费曼参数化 Feynman parameterization 的方法。

我们先从如下公式开始：

$\begin{aligned} \frac{1}{AB} &= \int_{0}^{1}dx \frac{1}{[xA+(1-x)B]^2}\\ &= \int_{0}^{1} dxdy \delta(x+y-1)\frac{1}{(xA+yB)^2} \end{aligned}$

这个公式是容易证明的：

$\begin{aligned} \int_{0}^{1}dx \frac{1}{[xA+(1-x)B]^2} &=\frac{1}{B-A} \frac{1}{xA+(1-x)B}|_{0}^{1}\\ &= \frac{1}{AB}\\ \end{aligned}$

将上式对 $B$ 求偏导，得到更一般的式子：

$\frac{1}{AB^n} = \int_{0}^{1} dxdy \delta(x+y-1)\frac{ny^{n-1}}{(xA+yB)^{n+1}}$

推广到多个因子的情形，可以使用数学归纳法推导：

$\frac{1}{A_1A_2\cdots A_n} = \int_{0}^{1} dx_1dx_2\cdots dx_n \delta(\Sigma x_i-1)\frac{(n-1)!}{(x_1A_1+x_2A_2+\cdots+x_nA_n)^n}$

对 $A_i$ 求 $m_i$ 次偏导，得到以下一般式子：

$\frac{1}{A_1^{m_1}A_2^{m_2}\cdots A_n^{m_n}} = \int_{0}^{1}dx_1\cdots dx_n \delta(\Sigma x_i -1)\frac{\prod x_i^{m_i-1}}{(\sum x_iA_i)^{\Sigma m_i}}\frac{\Gamma(m_1+\cdots+m_2)}{\Gamma(m_1)\cdots \Gamma(m_n)}$

这个公式在 $m_i$ 不为整数时仍然成立。

---

因此，可以将圈图积分 $(14)$ 的分母项写为：

$\frac{1}{((k-p)^2+i\epsilon)(k'^2-m^2+i\epsilon)(k^2-m^2+i\epsilon)} = \int_{0}^{1}dxdydz \delta(x+y+z-1)\frac{2}{D^3}$

其中 $D$ 为：

$\begin{aligned} D &= x(k^2-m^2) + y(k'^2-m^2) + z(k-p)^2 + (x+y+z)i\epsilon\\ &= k^2 + 2k\cdot(yq-zp) + yq^2 +zp^2 - (x+y)m^2 + i\epsilon\\ \end{aligned}$

其中已经代入 $x+y+z =1,k' = k+q$。

作代换：$l\equiv k+yq-zp$
得到：

$D = l^2 - \Delta + i\epsilon,\quad \Delta = -xyq^2+(1-z)^2m^2$

主要到在 $\Delta$ 项中，$q^2<0,\Delta > 0$，我们可以将其看作一个有效质量项。$D$ 仅仅依赖于 $l$ 的大小。根据对称性，注意到有以下式子成立：

$\begin{aligned} &\int \frac{d^4\mathcal{l}}{(2\pi)^4}\frac{\mathcal{l}^{\mu}}{D^3} = 0\\ &\int \frac{d^4\mathcal{l}}{(2\pi)^4}\frac{\mathcal{l}^{\mu}\mathcal{l}^{\nu}}{D^3} = \int \frac{d^4\mathcal{l}}{(2\pi)^4}\frac{\frac{1}{4}g^{\mu\nu}l^2}{D^3}\\ \end{aligned}$

圈图积分的分子为：

$\begin{aligned} &\bar{u}(p')(\cancel{k}\gamma^{\mu}\cancel{k}' + m^2\gamma^{\mu}- 2m(k+k')^{\mu})u(p)\\ &= \bar{u}(p')[-\frac{1}{2}\gamma^{\mu}l^2 + (-y\cancel{q}+z\cancel{p})\gamma^{\mu}((1-y)\cancel{q} + z\cancel{p}))\\ &\qquad + m^2\gamma^{\mu} - 2m((1-2y)q^{\mu}+2zp^{\mu})]u(p)\\ &= \bar{u}(p')(\gamma^{\mu}(-\frac{1}{2}l^2+(1-x)(1-y)q^2 + (1-2z-z^2)m^2)\\ &\qquad +(p'^{\mu} + p^{\mu})\cdot mz(z-1) + q^{\mu}\cdot m(z-2)(x-y) )u(p)\\ \end{aligned}$

最终一阶圈图的贡献可以写为：

$\begin{aligned} \bar{u}(p')\delta\Gamma^{\mu}(p',p)u(p) &= 2ie^2\int \frac{d^4l}{(2\pi)^4}\int_{0}^{1}dxdydz \delta(x+y+z-1)\frac{2}{D^3}\\ &\qquad \times \bar{u}(p')(\gamma^{\mu}(-\frac{1}{2}l^2+(1-x)(1-y)q^2 + (1-4z+z^2)m^2)\\ &\qquad \frac{i\sigma^{\mu\nu}q_{\nu}}{2m}(2m^2z(1-z)))u(p)\\ \end{aligned}$

现在我们需要计算对 $l^0$ 的积分。其极点为：$\pm(\sqrt{|\bm{l}|^2 + \Delta} - i\epsilon)$。然后再在球坐标下对空间求积分。不过这里，我们采用一个更为简单的方法进行计算。我们观察对 $l^0$ 的围线积分。考虑被积函数无穷远围线的贡献为零。因此，我们可以将整个积分围线逆时针旋转 $90\degree$。如此我们可以定义 Euclidean 四维变量 $l_E$：

$l^0 \equiv il_E^0;\quad \bm{l} = \bm{l}_E$

如此：$l^0$ 积分上下限 $\pm i\infty$ 对应于 $l_E^0$ 的积分上下限 $\pm\infty$。由此，我们可以使用四维球坐标计算上述积分。这种技巧称为 wick rotation。

我们先计算下述积分：

$\begin{aligned} \int \frac{d^4 l}{(2\pi)^4}\frac{1}{|l^2-\Delta|^m} &= \frac{i}{(-1)^m}\frac{1}{(2\pi)^4}\int d^4l_E\frac{1}{|l_E^2+\Delta|^m}\\ &= \frac{i(-1)^m}{(2\pi)^4}\int d\Omega_4 \int_{0}^{\infty}dl_E \frac{l_E^3}{|l_E^2 + \Delta|^m} \end{aligned}$

其中 $\int d\Omega_4$ 表示在一个四维球面上做积分。总的立体角为 $2\pi^2$。我们引入四维球坐标：

$\begin{aligned} &x = (r\sin\omega\sin\theta\cos\phi, r\sin\omega\sin\theta\sin\phi,r\sin\omega\cos\theta,r\cos\omega)\\ & \omega,\theta \in [0,\pi],\phi \in [0,2\pi) \end{aligned}$

积分体积元成为：

$d^4x = r^3\sin^2\omega\sin\theta d\phi d\theta d\omega dr$

那么上述积分很容易计算：

$\begin{aligned} &\frac{i(-1)^m}{(2\pi)^4}\int d\Omega_4 \int_{0}^{\infty}dl_E \frac{l_E^3}{|l_E^2 + \Delta|^m}\\ &= \frac{i(-1)^m}{(2\pi)^4}\cdot 2\pi^2 \cdot \int_{0}^{\infty} \frac{r^3dr}{|r^2+\Delta|^m}\\ &= \frac{i(-1)^m}{8\pi^2} \cdot \int_{0}^{\infty} \frac{(r^2+\Delta-\Delta)d(r^2+\Delta)}{2(r^2+\Delta)^m}\\ &= \frac{i(-1)^m}{16\pi^2} (\frac{-1}{m-2}\frac{1}{(r^2+\Delta)^{m-2}} + \frac{\Delta}{m-1}\frac{1}{(r^2+\Delta)^{m-1}})|_{0}^{\infty}\\ &= \frac{i(-1)^m}{(4\pi)^2}\frac{1}{(m-1)(m-2)}\frac{1}{\Delta^{m-2}} \end{aligned}$

类似的有：

$\int \frac{d^4 l}{(2\pi)^4}\frac{l^2}{|l^2-\Delta|^m} = \frac{i(-1)^{m-1}}{(4\pi)^2}\frac{2}{(m-1)(m-2)(m-3)}\frac{1}{\Delta^{m-3}}$

这个积分适用条件是 $m>3$。对于 $m=3$，wick rotation 不适用，积分将发散。但我们发现这正是我们所考虑的圈积分所对应的情形！为了解决这个问题，我们必须引入某种截断，因为场论本身也只是一个低能时的有效理论，那些高能区的物理将进入到与截断相关的耦合系数中去。我们考虑将其中的光子传播子进行替换：

$\frac{1}{(k-p)^2 +i\epsilon} \rightarrow \frac{1}{(k-p)^2 +i\epsilon}-\frac{1}{(k-p)^2-\Lambda^2 +i\epsilon}$

其中 $\Lambda$ 为一个很大的质量。我们添加了一项假想的重光子传播子。那么这个积分对于小动量不会有影响，而会在大动量 $k\gtrsim \Lambda$ 处截断。

对于包含重光子的圈积分，分子不需要进行修改，分母只需要进行如下替换：

$\Delta \longrightarrow \Delta_{\Lambda} = -xyq^2 + (1-z)^2m^2 + z\Lambda^2$

由此：

$\begin{aligned} \int \frac{d^4l}{(2\pi)^3}(\frac{l^2}{|l^2-\Delta|^3}-\frac{l^2}{|l^2-\Delta_{\Lambda}|^3}) &= \frac{i}{(4\pi)^2}\int_{0}^{\infty}dl_E^2 (\frac{l_E^4}{|l^2_E+\Delta|^3}-\frac{l_E^4}{|l_E^2+\Delta_{\Lambda}|^3})\\ &= \frac{i}{(4\pi)^2}\log(\frac{\Delta_{\Lambda}}{\Delta}) \end{aligned}$

这种引入假想的重光子传播子的方法称为 Pauli-Villars 正规化(Pauli-Villars regularization)。

那么最终得到的一阶圈图修正利用以上公式可以写为：

$\begin{aligned} &\frac{\alpha}{2\pi} \int_{0}^{1}dxdydz\delta(x+y+z-1)\\ &\times \bar{u}(p')(\gamma^{\mu}[\log \frac{z\Lambda^2}{\Delta} +\frac{1}{\Delta}((1-x)(1-y)q^2 + (1-4z+z^2)m^2]\\ &+ \frac{i\sigma^{\mu\nu}q_{\nu}}{2m}[\frac{1}{\Delta}2m^2z(1-z)])u(p)\\ \end{aligned}$

其中方括号内的就是所求的形状因子。但实际上，这个式子仍然是存在红外发散的（后面会详细说明），我们还要为光子引入一个不为零的小质量以构成红外截断。这意味着，对于 $1/\Delta$ 项，需要作替换：

$(k-p)^2 \rightarrow (k-p)^2 -\mu^2$

其中 $\mu$ 是一个小质量。

如此形状因子成为：

$\begin{aligned} F_1(q^2) =& 1 + \frac{\alpha}{2\pi}\int_{0}^{1}dxdydz\delta(x+y+z-1)\\ &\times [\log(\frac{m^2(1-z)^2}{m^2(1-z)^2 - q^2xy}) + \frac{m^2(1-4z+z^2)+q^2(1-x)(1-y)}{m^2(1-z)^2 - q^2xy + \mu^2z}]\\ &- \frac{m^2(1-4z+z^2)}{m^2(1-z)^2+\mu^2z}) + \mathcal{O}(\alpha^2)\\ &\\ F_2(q^2) &= \frac{\alpha}{2\pi}\int_{0}^{1}dxdydz\delta(x+y+z-1)(\frac{2m^2z(1-z)}{m^2((1-z)^2 -q^2xy)}) + \mathcal{O}(\alpha^2)\\ \end{aligned}$

注意到红外或紫外发散并不影响 $F_2(q^2)$，其中：

$\begin{aligned} F_2(q^2 = 0) &= \frac{\alpha}{2\pi}\int_{0}^{1}dxdydz\delta(x+y+z-1)(\frac{2m^2z(1-z)}{m^2((1-z)^2)})\\ &= \frac{\alpha}{\pi}\int_{0}^{1}dz\int_{0}^{1-z}dy \frac{z}{1-z}\\ &= \frac{\alpha}{2\pi}\\ \end{aligned}$

得到一阶圈图对 g-factor 的修正为：

$a_{e} \equiv \frac{g-2}{2} = \frac{\alpha}{2\pi} \approx 0.0011614$

对比实验值 $a_{e} = 0.0011597$，两者已经很接近了。我们可以考虑更高阶的圈图，使得计算更为精确。

红外发散

现在来考虑 $F_1(q^2)$ 中产生红外发散的项。

$\begin{aligned} F_1(q^2) \approx& \frac{\alpha}{2\pi}\int_{0}^{1}dxdydz\delta(x+y+z-1)\\ &[\frac{m^2(1-4z+z^2)+q^2(1-x)(1-y)}{m^2(1-z)^2 - q^2xy + \mu^2z}- \frac{m^2(1-4z+z^2)}{m^2(1-z)^2+\mu^2z})]\\ \end{aligned}\tag{5}$

在 $\mu\rightarrow 0$ 时，分母在 $z = 1,x = y = 0$ 时取得极值，该积分主要由这个极点附近的区域贡献。对于分子，我们直接令 $z = 1,x=y=0$，并且积掉 $\delta$ 函数：

$F_1(q^2) = \frac{\alpha}{2\pi}\int_0^1dz \int_{0}^{1-z}dy[\frac{-2m^2+q^2}{m^2(1-z)^2 - q^2xy + \mu^2}- \frac{-2m^2}{m^2(1-z)^2+\mu^2}]\tag{6}$

作代换：

$y = (1-z)\xi,\quad w=1-z$

$(6)$ 式成为：

$\begin{aligned} F_1(q^2) &= \frac{\alpha}{4\pi}\int_0^1d\xi \int_{0}^{1}d(w^2)(\frac{-2m^2+q^2}{(m^2- q^2(1-\xi)\xi)w^2 + \mu^2}- \frac{-2m^2}{m^2w^2+\mu^2})\\ &= \frac{\alpha}{4\pi}\int_{0}^{1}d\xi[(\frac{-2m^2+q^2}{m^2-q^2\xi(1-\xi)})\log(\frac{m^2-q^2\xi(1-\xi)}{\mu^2}) + 2\log(\frac{m^2}{\mu^2})] \end{aligned}\tag{7}$

在 $\mu\rightarrow 0$ 时，我们可以忽略对数中分子的细节。每一个正比于 $m^2$ 或 $-q^2$ 的项都是近似相同的。

$\begin{aligned} F_1(q^2) &= 1 - \frac{\alpha}{2\pi}f_{IR}(q^2)\log(\frac{-q^2\ or\ m^2}{\mu^2}) + \mathcal{O}(\alpha^2)\\ \end{aligned}$

其中：

$f_{IR}(q^2) = \int_{0}^{1}(\frac{m^2 - q^2/2}{m^2 - q^2\xi(1-\xi)})d\xi - 1$

由于 $\xi(1-\xi)$ 的最大值为 $\frac{1}{4}$，因此 $f_{IR}(q^2) > 0$。

我们在作顶点修正时实际在作如下替换：

$-e\gamma^{\mu} \rightarrow -e\gamma^{\mu} F_1(q^2)$

这等价于将电子电量 $e$ 替换成 $eF_1(q^2)$。因此对散射截面的顶点修正成为：

$\begin{aligned} \frac{d\sigma}{d\Omega} \simeq (\frac{d\sigma}{d\Omega})_0 \cdot [1 - \frac{\alpha}{\pi}f_{IR}(q^2)\log(\frac{-q^2\ or\ m^2}{\mu^2}) + \mathcal{O}(\alpha^2)]\\ \end{aligned}\tag{8}$

我们现在对 $F_1(q^2)$ 进行一下估计，在 $-q^2\rightarrow \infty$ 时，有：

$\begin{aligned} f_{IR}(q^2) &= \int_{0}^{1}(\frac{m^2 - q^2/2}{m^2 - q^2\xi(1-\xi)})d\xi\\ &\rightarrow \frac{1}{2}\int_{0}^{1}\frac{- q^2}{m^2 - q^2\xi(1-\xi)}d\xi\\ &\sim \frac{1}{2}(\int_{0}\frac{- q^2}{m^2 - q^2\xi}d\xi + \int^{1}\frac{- q^2}{m^2 - q^2(1-\xi)}d\xi)\\ &\sim \log(\frac{-q^2}{m^2})\\ \end{aligned}$

代入 $(8)$ 式，得到：

$\begin{aligned} \frac{d\sigma}{d\Omega} (p\rightarrow p') = (\frac{d\sigma}{d\Omega})_0 \cdot [1 - \frac{\alpha}{\pi}\log(\frac{-q^2}{m^2})\log(\frac{-q^2}{\mu^2}) + \mathcal{O}(\alpha^2)]\\ \end{aligned}\tag{9}$

考虑上一篇计算出的轫致辐射的微分散射截面：

$\begin{aligned} \frac{d\sigma}{d\Omega} (p\rightarrow p' + \gamma) = (\frac{d\sigma}{d\Omega})_0 \cdot [+\frac{\alpha}{\pi}\log(\frac{-q^2}{m^2})\log(\frac{-q^2}{\mu^2}) + \mathcal{O}(\alpha^2)]\\ \end{aligned}\tag{10}$

单单看顶点修正后的弹性散射微分散射截面或是轫致辐射的微分散射截面，它们都是发散的，因为 $\mu\rightarrow 0$。但是它们的总和是收敛的。其中的物理原因是十分深刻的：因为我们不能单独观测到轫致辐射或是弹性散射。对于任何一个探测设备来说，其都存在一定的探测能量的下限 $E_l$。如此，测量得到的弹性散射截面实际上是：

$(\frac{d\sigma}{d\Omega})(p\rightarrow p') + (\frac{d\sigma}{d\Omega})(p\rightarrow p' + \gamma(k<E_l)) \equiv (\frac{d\sigma}{d\Omega})_{measured}$

这个微分散射截面为：

$\begin{aligned} (\frac{d\sigma}{d\Omega})_{measured} \approx (\frac{d\sigma}{d\Omega})_0[&1-\frac{\alpha}{\pi}f_{IR}(q^2)\log(\frac{-q^2\ or\ m^2}{\mu^2})\\ &+\frac{\alpha}{2\pi}\mathcal{I}(\bm{v},\bm{v}')\log(\frac{E_l^2}{\mu^2}) + \mathcal{O}(\alpha^2)] \end{aligned}$

在 $-q^2\gg m^2$ 时，有 $\mathcal{I}(\bm{v},\bm{v}') = 2f_{IR}(q^2)$，此时上式成为：

$(\frac{d\sigma}{d\Omega})_{measured} \approx (\frac{d\sigma}{d\Omega})_0[1-\frac{\alpha}{\pi}f_{IR}(q^2)\log(\frac{-q^2\ or\ m^2}{E_l^2})+ \mathcal{O}(\alpha^2)]\tag{11}$

这将成为一个有限的项。

这里说明 $\mathcal{I}(\bm{v},\bm{v}') = 2f_{IR}(q^2)$：

$\mathcal{I}(\bm{v},\bm{v}') = \int \frac{d\Omega_{\bm{k}}}{4\pi}(\frac{2p\cdot p'}{(\hat{k}\cdot p')(\hat{k}\cdot p)} - \frac{m^2}{(\hat{k}\cdot p')^2} - \frac{m^2}{(\hat{k}\cdot p)^2})$

对于后两项，我们计算得到：

$\begin{aligned} \int \frac{d\Omega_{\bm{k}}}{4\pi}\frac{1}{(\hat{k}\cdot p)^2} &= \frac{1}{2} \int_{-1}^{1}d\cos\theta \frac{1}{(p^0 - p\cos\theta)^2}\\ &= \frac{1}{2p} \frac{1}{p^0 - p\cos\theta}|_{-1}^{1} = \frac{1}{m^2}\\ \end{aligned}$

对于第一项，通过费曼参数化得到：

$\begin{aligned} \int \frac{d\Omega_{\bm{k}}}{4\pi}\frac{2p\cdot p'}{(\hat{k}\cdot p')(\hat{k}\cdot p)} &= \int_{0}^{1}d\xi \int \frac{d\Omega_{\bm{k}}}{4\pi} \frac{1}{[\xi\hat{k}\cdot p' + (1-\xi)\hat{k}\cdot p]^2}\\ &= \int_{0}^{1}d\xi \int \frac{d\Omega_{\bm{k}}}{4\pi} \frac{1}{[\hat{k}\cdot(\xi p' + (1-\xi)p)]^2}\\ &= \int_{0}^{1}d\xi \frac{1}{(\xi p' + (1-\xi)p)^2}\\ &= \int_{0}^1d\xi \frac{1}{m^2-\xi(1-\xi)q^2} \end{aligned}$

将这三项加起来就得到：

$\mathcal{I}(\bm{v},\bm{v}') = 2f_{IR}(q^2)$

这里仍然存在问题需要进行说明：

1. 在超过领头阶的范围内，轫致辐射与电子弹性散射的散射截面中的发散能否相消呢？

2. 如何解释出现在 $(11)$ 式中出现的散射截面对能量下限 $E_l$ 的依赖？

3. 如何得到轫致辐射的粒子数？

对于这些问题，可以参考 an introduction to Quantum Field Theory,peskin 6.5 小节的讨论。下面仅仅展示最后得到的结果：对于发射 $n$ 个 soft photons 的情况，且他们的能量介于 $E_{-}$ 与 $E_{+}$ 之间（高于 $E_+$ 的成为 hard photon）。那么我们需要将弹性散射截面乘以以下因子：

$Prob(n\gamma\ with\ E_{-}<E<E_{+}) = \frac{1}{n!}[\frac{\alpha}{\pi}f_{IR}(q^2)\log(\frac{E_{+}^2}{E_{-}^2})]^2\exp[-\frac{\alpha}{\pi}f_{IR}(q^2)\log(\frac{E_{+}^2}{E_{-}^2})]$

平均辐射光子数为：

$\langle n\rangle = \frac{\alpha}{\pi}\log(\frac{E_{+}}{E_{-}})\mathcal{I}(\bm{v},\bm{v}')$