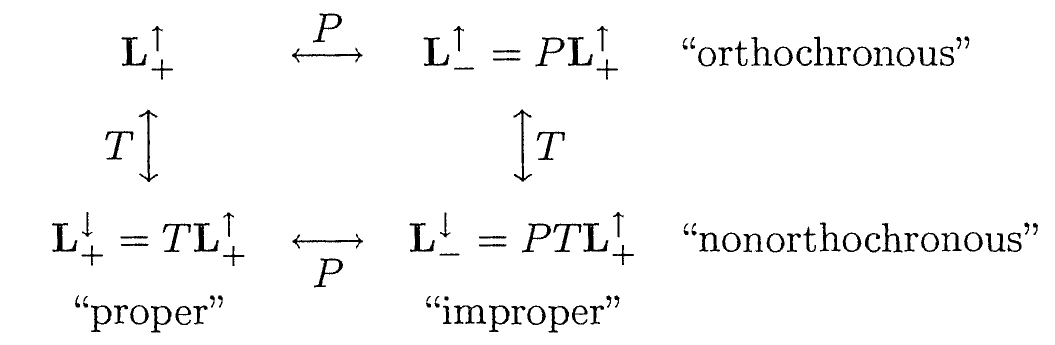之前，我们所讨论的是连续对称性对应的连续洛伦兹变换。在此，我们继续讨论离散对称性所对应的变换以及相应的性质。一般来说，一个对称变换可以用一个线性幺正矩阵或一个反线性反幺正矩阵来表示[1]^{[1]}。对于连续对称变换，我们总要求任何变换总与恒等变换相连通，因此其只能对应线性幺正矩阵，在前面我们总是默认这一点。而离散对称群并不具有李群结构。

反线性含义为：

U(aψ1+bψ2)=a∗Uψ1+b∗Uψ2U(a\psi_1 + b\psi_2) = a^*U\psi_1 + b^*U\psi_2

反幺正含义为：

⟨UΦ∣UΨ⟩=⟨Φ∣Ψ⟩∗\langle U\Phi|U\Psi\rangle = \langle\Phi| \Psi\rangle^*

我们现在需要考虑的离散变换为：

  • 宇称变换 PP (parity)

(t,x)→(t,−x)(1)(t,\bm{x})\rightarrow(t,-\bm{x})\tag{1}

  • 时间反演 TT (time reversal)

(t,x)→(−t,x)(2)(t,\bm{x})\rightarrow(-t,\bm{x})\tag{2}

连续洛伦兹变换实际对应 正规正时洛伦兹群 proper, orthochronous Lorentz group L+↑\bm{L}_{+}^{\uparrow}。宇称变换与时间反演将洛伦兹群的四个不连通的子群联系起来。

另外，还有一种离散变换(非时空)，它完成了正反粒子间的变换。为 电荷共轭对称 (charge conjugation)，记作 CC。

目前已知自然界中的四种基本相互作用中的三种：电磁力，强相互作用，引力在 C,P,TC,P,T 变换下是不变。而弱相互作用在 CPTCPT 联合变换下保持不变。

离散时空变换

考虑将宇称变换、时间反演的数学表达式 (1)(2)(1)(2) 用四矢量改写：

xμ⟶Px′μ=P   νμxνxμ⟶Tx′μ=T   νμxν\begin{aligned} &x^{\mu} \overset{P}{\longrightarrow} x'^{\mu} = \mathscr{P}^{\mu}_{\ \ \ \nu}x^{\nu}\\ &x^{\mu} \overset{T}{\longrightarrow} x'^{\mu} = \mathscr{T}^{\mu}_{\ \ \ \nu}x^{\nu}\\ \end{aligned}

其中：

P   νμ=(10000−10000−10000−1)T   νμ=(−1000010000100001)\mathscr{P}^{\mu}_{\ \ \ \nu} = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\\ \end{pmatrix}\quad\mathscr{T}^{\mu}_{\ \ \ \nu} = \begin{pmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix}

类似庞加莱变换的记号 U(Λ,a)U(\Lambda,a)，我们将一个 nn 维的变换矩阵表示为：

P≡U(P,0)T≡U(T,0)P \equiv U(\mathscr{P},0)\quad T \equiv U(\mathscr{T},0)

容易得到：

PU(Λ,a)P−1=U(PΛP−1,Pa)TU(Λ,a)T−1=T(TΛT−1,Ta)\begin{aligned} PU(\Lambda,a)P^{-1} = U(\mathscr{P}\Lambda\mathscr{P}^{-1},\mathscr{P}a)\\ TU(\Lambda,a)T^{-1} = T(\mathscr{T}\Lambda\mathscr{T}^{-1},\mathscr{T}a)\\ \end{aligned}

类似于我们在 量子场论笔记（四）：洛伦兹变换及其代数结构 中所计算的一样。当 Λ\Lambda 与 aa 为无穷小量时，可以得到对对庞加莱群生成元 Jμν,PμJ^{\mu\nu},P^{\mu} 的变换规则：

PiJρσP−1=iPμ   ρPν   σJμνPiPρP−1=iPμ   ρPμTiJρσT−1=iTμ   ρTν   σJμνTiPρT−1=iTμ   ρPμ(3)\begin{aligned} &PiJ^{\rho\sigma}P^{-1} = i\mathscr{P}_{\mu}^{\ \ \ \rho}\mathscr{P}_{\nu}^{\ \ \ \sigma}J^{\mu\nu}\\ &PiP^{\rho}P^{-1} = i\mathscr{P}_{\mu}^{\ \ \ \rho}P^{\mu}\\ &TiJ^{\rho\sigma}T^{-1} = i\mathscr{T}_{\mu}^{\ \ \ \rho}\mathscr{T}_{\nu}^{\ \ \ \sigma}J^{\mu\nu}\\ &TiP^{\rho}T^{-1} = i\mathscr{T}_{\mu}^{\ \ \ \rho}P^{\mu}\\ \end{aligned}\tag{3}

现在我们需要确定 P,TP,T 是线性幺正矩阵还是反线性反幺正矩阵。我们作如下考虑：设 ψ\psi 为哈密顿量 HH 本征值为 EE 的本征态，即：

Hψ=Eψ(4)H\psi = E\psi \tag{4}

作宇称变换得到：

PHψ=PHP−1Pψ=EPψPH\psi = PHP^{-1} P\psi = EP\psi

考虑到 PψP\psi 应当也是 HH 的正能量本征态。因此得到：

PHP−1=H(5)PHP^{-1} = H \tag{5}

同理对于时间反演也有：

THT−1=H(6)THT^{-1} = H \tag{6}

(5)(6)(5)(6) 将确定 P,TP,T 的性质。根据 (3)(3) 中第 2,42,4 式，取 ρ=0\rho = 0，得到：

PiHP−1=iHTiHT−1=−iH(7)\begin{aligned} & PiHP^{-1} = iH\\ & TiHT^{-1} = -iH\\ \end{aligned}\tag{7}

那么得到：PP 为线性矩阵、TT 为反线性矩阵。将这一性质运用到 (3)(3) 式中，得到对于其他生成元的变换：

PJP−1=+JPKP−1=−KPPP−1=−PTJT−1=−JTKT−1=+KTPT−1=−PPHP−1=THT−1=P(8)\begin{aligned} &P\bm{J}P^{-1} = +\bm{J}\\ &P\bm{K}P^{-1} = -\bm{K}\\ &P\bm{P}P^{-1} = -\bm{P}\\ &T\bm{J}T^{-1} = -\bm{J}\\ &T\bm{K}T^{-1} = +\bm{K}\\ &T\bm{P}T^{-1} = -\bm{P}\\ &PHP^{-1} = THT^{-1} = P\\ \end{aligned}\tag{8}

我们发现：

  • 宇称变换使动量反向，不改变角动量。
  • 时间反演使动量、角动量均反向（包括自旋）。

下面，我们来具体讨论自由粒子解、阶梯算子在宇称变换与时间反演下如何变换。

宇称变换

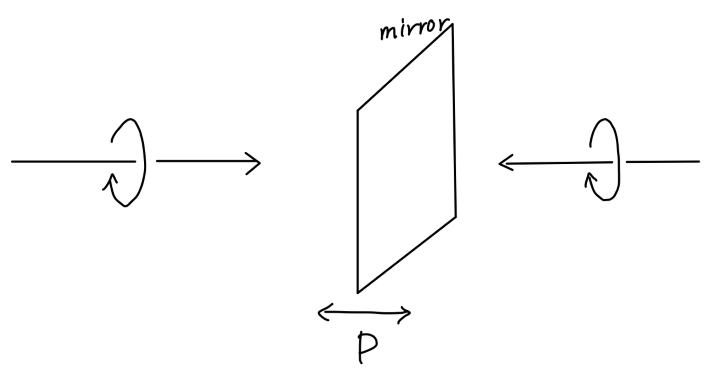
PP 变换完成了以下操作：

aps†∣0⟩⟶Pa−ps†∣0⟩(9)a_{\bm{p}}^{s\dagger}|0\rangle \overset{P}{\longrightarrow} a_{\bm{-p}}^{s\dagger}|0\rangle \tag{9}

(9)(9) 式等价为：

PapsP=ηaa−psPbpsP=ηbb−ps(10)Pa_{\bm{p}}^{s}P = \eta_a a_{-\bm{p}}^{s}\quad Pb_{\bm{p}}^{s}P = \eta_b b_{-\bm{p}}^{s}\tag{10}

由于经过两次宇称变换后，物理量的观测值将不发生改变。由于物理量总是由偶数个场量组成，这等将于阶梯算子将回到自身或添加一个负号。因此可得：

ηa2=ηb2=±1\eta_a^2 = \eta_b^2 = \pm 1

这样波函数在宇称变换下成为：

Pψ(x)P=∫d3p(2π)312Ep∑s(PapsPus(p)e−ipx+Pbps†Pvs(p)eipx)=∫d3p(2π)312Ep∑s(ηaapsus(p)e−ipx+ηb∗bps†vs(p)eipx)(11)\begin{aligned} P\psi(x)P &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (Pa_{\bm{p}}^{s}P u^s(p)e^{-ipx}+Pb_{\bm{p}}^{s\dagger}P v^s(p)e^{ipx})\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (\eta_{a}a_{\bm{p}}^{s}u^s(p)e^{-ipx}+\eta_b^* b_{\bm{p}}^{s\dagger} v^s(p)e^{ipx})\\ \end{aligned}\tag{11}

注意这里对波函数的变换与对 (5)(5) 式态矢变换的差别。

我们来看 ηa,ηb\eta_a,\eta_b 需要满足的性质。我们使用 p~=(p0,−p)\tilde{p} = (p^0,-\bm{p}) 来表示波函数。考虑到：

u(p)=(p⋅σξp⋅σˉξ)=(p~⋅σˉξp~⋅σξ)=γ0u(p~)v(p)=(p⋅σξ−p⋅σˉξ)=(p~⋅σˉξ−p~⋅σξ)=−γ0v(p~)(12)\begin{aligned} &u(p) = \begin{pmatrix} \sqrt{p\cdot\sigma} \xi\\ \sqrt{p\cdot \bar{\sigma}} \xi\\ \end{pmatrix}= \begin{pmatrix} \sqrt{\tilde{p}\cdot\bar{\sigma}} \xi\\ \sqrt{\tilde{p}\cdot \sigma} \xi\\ \end{pmatrix} = \gamma^0 u(\tilde{p})\\ &v(p) = \begin{pmatrix} \sqrt{p\cdot\sigma} \xi\\ -\sqrt{p\cdot \bar{\sigma}} \xi\\ \end{pmatrix}= \begin{pmatrix} \sqrt{\tilde{p}\cdot\bar{\sigma}} \xi\\ -\sqrt{\tilde{p}\cdot \sigma} \xi\\ \end{pmatrix} = -\gamma^0 v(\tilde{p})\\ \end{aligned}\tag{12}

那么可以将 (11)(11) 式写为：

∫d3p(2π)312Ep∑s(ηaapsγ0us(p~)e−ip~(t,−x)−ηb∗bps†γ0vs(p~)eip~⋅(t,−x))=Cψ(t,−x)\begin{aligned} &\int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (\eta_{a}a_{\bm{p}}^{s}\gamma^0 u^s(\tilde{p})e^{-i\tilde{p}(t,-\bm{x})} - \eta_b^* b_{\bm{p}}^{s\dagger} \gamma^0 v^s(\tilde{p})e^{i \tilde{p}\cdot (t,-\bm{x})})\\ &= C \psi(t,-\bm{x}) \end{aligned}

上式中 CC 是一个常数矩阵，那么这意味着：

ηb∗=−ηa⇒ηaηb=−ηaηa∗=−1(13)\eta_b^* = -\eta_a \Rightarrow \eta_a\eta_b = -\eta_a\eta_a^* = -1 \tag{13}

如此，波函数的宇称变换最终可以表示为：

Pψ(t,x)P=ηaγ0ψ(t,−x)(14)P\psi(t,\bm{x})P = \eta_a\gamma^0\psi(t,-\bm{x}) \tag{14}

ηa\eta_a 是一个仅仅与粒子种类有关的量，称为粒子的 本征宇称 intrinsic parity。不失一般性的，我们可以设置：

ηa=1,ηb=−1\eta_a = 1,\quad \eta_b = -1

例如考虑如下态进行宇称变换：

aps†bqs′†∣0⟩⟶Pηaηba−ps†b−qs′†∣0⟩=−a−ps†b−qs′†∣0⟩a_{\bm{p}}^{s\dagger}b_{\bm{q}}^{s'\dagger}|0\rangle \overset{P}{\longrightarrow} \eta_a\eta_b a_{-\bm{p}}^{s\dagger}b_{-\bm{q}}^{s'\dagger}|0\rangle = -a_{-\bm{p}}^{s\dagger}b_{-\bm{q}}^{s'\dagger}|0\rangle

因此：一个由正反粒子对构成的束缚态的宇称为 −1-1。

我们接下来考虑对 Dirac 双线性映射的宇称变换。

  • ψˉ\bar{\psi}

PψˉP=Pψ†Pγ0=(PψP)†γ0=ηa∗ψˉ(t,−x)γ0\begin{aligned} P\bar{\psi}P &= P\psi^\dagger P\gamma^0\\ &= (P\psi P)^\dagger\gamma^0\\ &= \eta_a^* \bar{\psi}(t,-\bm{x}) \gamma^0\\ \end{aligned}

  • ψˉψ\bar{\psi}\psi

PψˉψP=(PψˉP)(PψP)=(ηa∗ψˉ(t,−x)γ0)(ηaγ0ψ(t,−x))=ψˉψ(t,−x)\begin{aligned} P\bar{\psi}\psi P &= (P\bar{\psi}P)(P\psi P)\\ &= (\eta_a^* \bar{\psi}(t,-\bm{x}) \gamma^0) (\eta_a\gamma^0\psi(t,-\bm{x}))\\ &= \bar{\psi}\psi(t,-\bm{x})\\ \end{aligned}

  • ψˉγμψ\bar{\psi}\gamma^{\mu}\psi

PψˉγμψP=ψˉγ0γμγ0ψ(t,−x)={+ψˉγμψ(t,−x)μ=0−ψˉγμψ(t,−x)μ=1,2,3\begin{aligned} P\bar{\psi}\gamma^{\mu}\psi P &= \bar{\psi}\gamma^{0}\gamma^{\mu}\gamma^{0}\psi(t,-\bm{x})\\ &=\left\{ \begin{aligned} & + \bar{\psi} \gamma^\mu \psi(t,-\bm{x})\quad \mu = 0\\ & -\bar{\psi} \gamma^\mu \psi(t,-\bm{x}) \quad \mu =1,2,3\\ \end{aligned}\right. \end{aligned}

  • ψˉγ5ψ\bar{\psi}\gamma^5\psi

Pψˉγ5ψP=(PψˉP)γ5(PψP)=ηa∗ψˉ(t,−x)γ0γ5ηaγ0ψ(t,−x)=−ψˉγ5ψ(t,−x)\begin{aligned} P\bar{\psi}\gamma^5\psi P &= (P\bar{\psi} P) \gamma^5 (P\psi P)\\ &= \eta_a^* \bar{\psi}(t,-\bm{x}) \gamma^0 \gamma^5 \eta_a\gamma^0\psi(t,-\bm{x})\\ &= -\bar{\psi}\gamma^5\psi(t,-\bm{x})\\ \end{aligned}

  • ψˉγμγ5ψ\bar{\psi}\gamma^{\mu}\gamma^5\psi

Pψˉγμγ5ψP=(PψˉP)γμγ5(PψP)=ηa∗ψˉ(t,−x)γ0γμγ5ηaγ0ψ(t,−x)={−ψˉγμγ5ψ(t,−x)μ=0+ψˉγμγ5ψ(t,−x)μ=1,2,3\begin{aligned} P\bar{\psi}\gamma^{\mu}\gamma^5\psi P &= (P\bar{\psi} P) \gamma^{\mu}\gamma^5 (P\psi P)\\ &= \eta_a^* \bar{\psi}(t,-\bm{x}) \gamma^0 \gamma^{\mu}\gamma^5 \eta_a\gamma^0\psi(t,-\bm{x})\\ &=\left\{ \begin{aligned} & - \bar{\psi} \gamma^\mu\gamma^{5} \psi(t,-\bm{x})\quad \mu = 0\\ & + \bar{\psi} \gamma^\mu \gamma^{5}\psi(t,-\bm{x}) \quad \mu =1,2,3\\ \end{aligned}\right. \end{aligned}

这里我们发现赝矢量、赝标量与矢量、标量相比，在宇称变换下符号相反。

时间反演

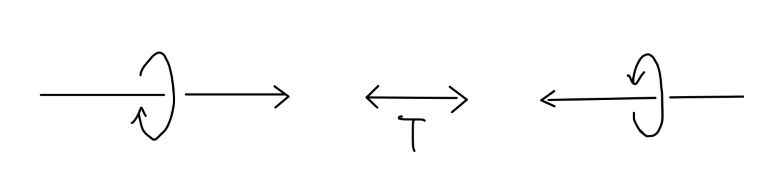
时间反演可以用一个反线性反幺正算符表示。我们之前得到：时间反演变换将使得动量、自旋反向。

为了描述自旋反向这件事，我们需要对自旋的表示进行进一步说明。之前我们用 s=1,2s=1,2 表示独立的两个自旋态。即：

ξ1=(10)≡∣0⟩ξ2=(01)≡∣1⟩\xi^1 = \begin{pmatrix} 1\\ 0\\ \end{pmatrix} \equiv |0\rangle\quad \xi^2 = \begin{pmatrix} 0\\ 1\\ \end{pmatrix} \equiv |1\rangle

那么任意一个自旋态可以表示为：

ξ=α∣0⟩+β∣1⟩\xi = \alpha|0\rangle + \beta|1\rangle

其中 α,β∈C,∣α∣2+∣β∣2=1\alpha,\beta\in\mathbb{C},|\alpha|^2+|\beta|^2=1。对自旋态 ξ\xi 的旋转构成一个 SU(2)SU(2) 群，这和 O(3)O(3) 群同构，于是我们在一个球面上表示任意自旋态。这称为 布洛赫球 bloch sphere。

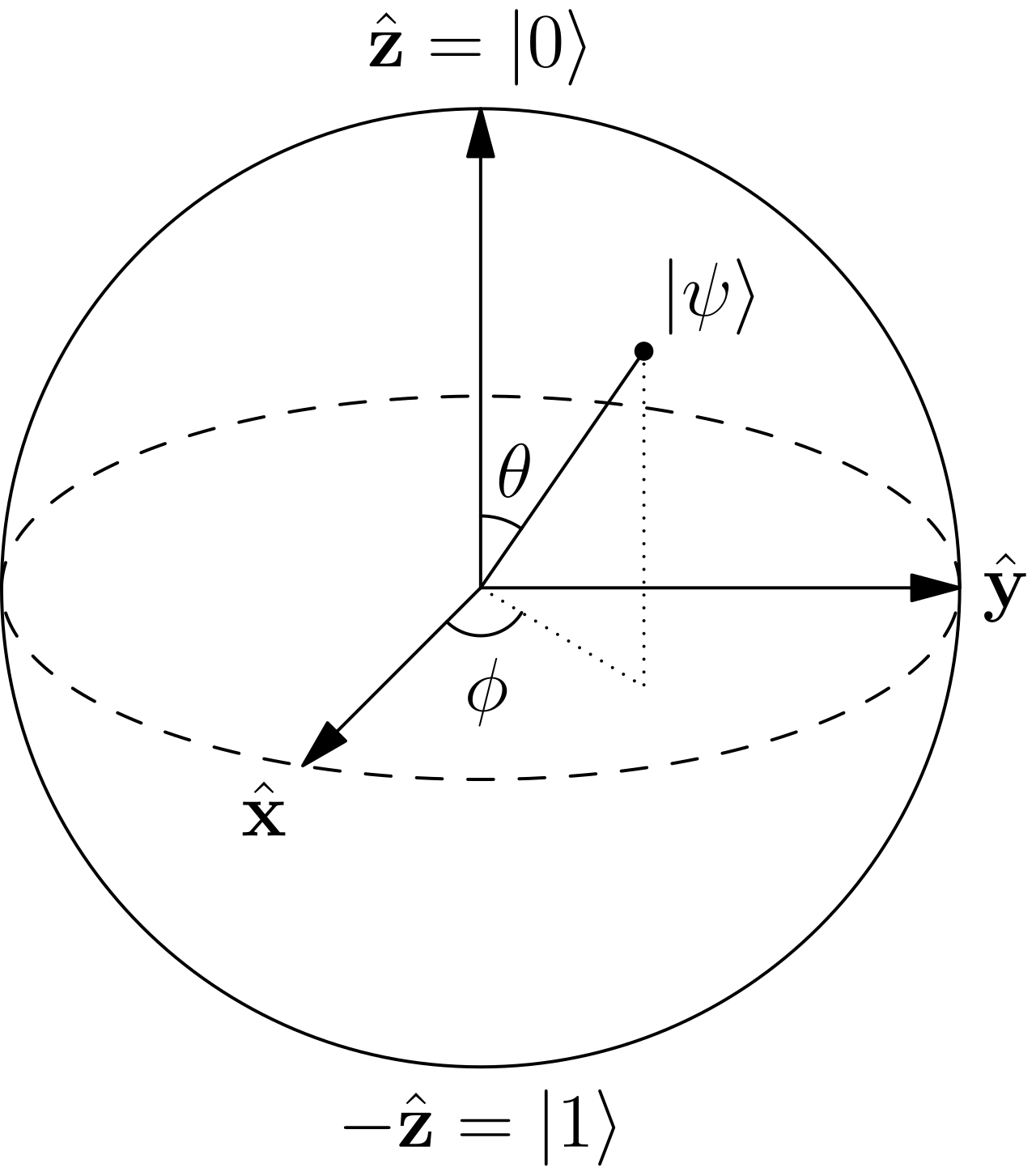
那么可以使用 θ,ϕ\theta,\phi 来表示一个任意方向的自旋态：

ξ(↑)=(cos⁡θ2eiϕsin⁡θ2)\xi(\uparrow) = \begin{pmatrix} \cos\frac{\theta}{2}\\ e^{i\phi}\sin\frac{\theta}{2}\\ \end{pmatrix}

以及与之反向的自旋态：

ξ(↓)=(−e−iϕsin⁡θ2cos⁡θ2)\xi(\downarrow) = \begin{pmatrix} -e^{-i\phi}\sin\frac{\theta}{2}\\ \cos\frac{\theta}{2}\\ \end{pmatrix}

我们定义：

ξs=(ξ(↑),ξ(↓))ξ−s=−iσ2(ξs)∗=(ξ(↓),−ξ(↑))(15)\begin{aligned} &\xi^s = (\xi(\uparrow),\xi(\downarrow))\\ &\xi^{-s} = -i\sigma^2(\xi^s)^* = (\xi(\downarrow),-\xi(\uparrow))\\ \end{aligned}\tag{15}

不难验证：若 ξ\xi 为 n⋅σ\bm{n}\cdot\bm{\sigma} 自旋为 +1+1 的本征态，那么：

(n⋅σ)(−iσ2ξ∗)=iσ2(n⋅σ∗)(ξ∗)=iσ2ξ∗=−(−iσ2ξ∗)(\bm{n}\cdot\bm{\sigma})(-i\sigma^2\xi^*) = i\sigma^2(\bm{n}\cdot\bm{\sigma}^*)(\xi^*) = i\sigma^2\xi^{*} = -(-i\sigma^2\xi^{*})

即 iσ2ξ∗i\sigma^2\xi^{*} 为 n⋅σ\bm{n}\cdot\bm{\sigma} 自旋为 −1-1 的本征态。

我们选取反粒子的自旋基底为 ξ−s,s=1,2\xi^{-s},s=1,2。

如此正/反粒子旋量可以分别表示为：

us(p)=(p⋅σξsp⋅σˉξs)vs(p)=(p⋅σξ−s−p⋅σˉξ−s)(16)\begin{aligned} u^s(p) &= \begin{pmatrix} \sqrt{p\cdot\sigma}\xi^{s}\\ \sqrt{p\cdot\bar{\sigma}}\xi^{s}\\ \end{pmatrix}\\ v^s(p) &= \begin{pmatrix} \sqrt{p\cdot\sigma}\xi^{-s}\\ -\sqrt{p\cdot\bar{\sigma}}\xi^{-s}\\ \end{pmatrix}\\ \end{aligned}\tag{16}

根据 (15)(15) 式，我们定义湮灭算子：

ap−s=(ap2,−ap1)bp−s=(bp2,−bp1)a_{\bm{p}}^{-s} = (a_{\bm{p}}^2,-a_{\bm{p}}^1)\quad b_{\bm{p}}^{-s} = (b_{\bm{p}}^2,-b_{\bm{p}}^1)

计算时间反演后的 us(p)u^s(p)：

以下将用到等式 p~⋅σσ2=σ2p⋅σ∗\sqrt{\tilde{p}\cdot\sigma}\sigma^2 = \sigma^2\sqrt{p\cdot\sigma^*}

u−s(p~)=(p~⋅σξ−sp~⋅σˉξ−s)=(p~⋅σ(−iσ2(ξs)∗)p~⋅σˉ(−iσ2(ξs)∗))=(−iσ2p⋅σ∗ξs∗−iσ2p⋅σˉ∗ξs∗)=−i(σ200σ2)[us(p)]∗=−γ1γ3[us(p)]∗(17)\begin{aligned} u^{-s}(\tilde{p}) &= \begin{pmatrix} \sqrt{\tilde{p}\cdot\sigma}\xi^{-s}\\ \sqrt{\tilde{p}\cdot\bar{\sigma}}\xi^{-s}\\ \end{pmatrix}\\ &= \begin{pmatrix} \sqrt{\tilde{p}\cdot\sigma}(-i\sigma^2(\xi^s)^*)\\ \sqrt{\tilde{p}\cdot\bar{\sigma}}(-i\sigma^2(\xi^s)^*)\\ \end{pmatrix}\\ &= \begin{pmatrix} -i\sigma^2\sqrt{p\cdot\sigma^*}\xi^{s*}\\ -i\sigma^2\sqrt{p\cdot\bar{\sigma}^*}\xi^{s*}\\ \end{pmatrix}\\ &= -i\begin{pmatrix} \sigma^2 & 0\\ 0 & \sigma^2\\ \end{pmatrix}[u^s(p)]^* = -\gamma^1\gamma^3[u^s(p)]^*\\ \end{aligned}\tag{17}

类似有：

v−s(p~)=−γ1γ3[vs(p)]∗(18)v^{-s}(\tilde{p}) = -\gamma^1\gamma^3[v^s(p)]^*\tag{18}

湮灭算子在时间反演下的形式为：

TapsT=a−p−sTbpsT=b−p−s(19)\begin{aligned} Ta_{\bm{p}}^sT = a_{-\bm{p}}^{-s}\\ Tb_{\bm{p}}^sT = b_{-\bm{p}}^{-s}\\ \end{aligned}\tag{19}

可以说明：这里引入一个相位因子将对结果无任何影响。

计算波函数的时间反演变换：

Tψ(t,x)T=∫d3p(2π)312Ep∑sT(apsus(p)e−ipx+bps†vs(p)eipx)T=∫d3p(2π)312Ep∑s(a−p−s[us(p)]∗eipx+b−p−s†[vs(p)]∗e−ipx)=−γ1γ3∫d3p~(2π)312Ep~∑s(ap~−su−s(p~)eip~(t,−x)+bp~−s†v−s(p~)e−ip~(t,−x))=−γ1γ3ψ(−t,x)\begin{aligned} T\psi(t,\bm{x})T &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s T(a_{\bm{p}}^{s} u^s(p)e^{-ipx}+b_{\bm{p}}^{s\dagger}v^s(p)e^{ipx})T\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (a_{-\bm{p}}^{-s} [u^s(p)]^*e^{ipx}+b_{-\bm{p}}^{-s\dagger}[v^s(p)]^*e^{-ipx})\\ &= -\gamma^1\gamma^3 \int \frac{d^3\tilde{p}}{(2\pi)^3}\frac{1}{\sqrt{2E_{\tilde{p}}}}\sum_s (a_{\tilde{p}}^{-s} u^{-s}(\tilde{p}) e^{i\tilde{p}(t,-\bm{x})} + b_{\tilde{p}}^{-s\dagger} v^{-s}(\tilde{p}) e^{-i\tilde{p}(t,-\bm{x})} )\\ &= -\gamma^1\gamma^3\psi(-t,\bm{x}) \end{aligned}

我们接下来考虑对 Dirac 双线性映射作时间反演。

  • ψˉ\bar{\psi}

TψˉT=Tψ†γ0T=(TψT)†(γ0)∗=(TψT)†(γ0)∗=−ψ†(−t,x)(γ1γ3)†γ0=−ψ†(−t,x)γ3γ1γ0=−ψ†(−t,x)γ0γ3γ1=−ψˉ(−t,x)γ3γ1\begin{aligned} T\bar{\psi}T &= T\psi^\dagger\gamma^0T\\ & = (T\psi T)^\dagger (\gamma^0)^*\\ & = (T\psi T)^\dagger (\gamma^0)^*\\ & = -\psi^\dagger(-t,\bm{x})(\gamma^1\gamma^3)^\dagger\gamma^0\\ & = -\psi^\dagger(-t,\bm{x})\gamma^3\gamma^1\gamma^0\\ & = -\psi^\dagger(-t,\bm{x})\gamma^0\gamma^3\gamma^1\\ & = -\bar{\psi}(-t,\bm{x})\gamma^3\gamma^1\\ \end{aligned}

  • ψˉψ\bar{\psi}\psi

TψˉψT=(TψˉT)(TψT)=(−ψˉ(−t,x)γ3γ1)(−γ1γ3ψ(−t,x))=ψˉψ(−t,x)\begin{aligned} T\bar{\psi}\psi T &= (T\bar{\psi}T)(T\psi T)\\ &=(-\bar{\psi}(-t,\bm{x})\gamma^3\gamma^1)(-\gamma^1\gamma^3\psi(-t,\bm{x}))\\ &= \bar{\psi}\psi(-t,\bm{x}) \end{aligned}

  • ψˉγμψ\bar{\psi}\gamma^{\mu}\psi

TψˉγμψT=(TψˉT)(γμ)∗(TψT)=ψˉ(γ3γ1)(γμ)∗(γ1γ3)ψ(−t,x)={+ψˉγμψ(−t,x)μ=0−ψˉγμψ(−t,x)μ=1,2,3\begin{aligned} T\bar{\psi}\gamma^{\mu}\psi T &= (T\bar{\psi}T)(\gamma^{\mu})^*(T\psi T)\\ &= \bar{\psi}(\gamma^3\gamma^1)(\gamma^{\mu})^*(\gamma^1\gamma^3)\psi(-t,\bm{x})\\ &= \left\{\begin{aligned} & +\bar{\psi}\gamma^{\mu}\psi(-t,\bm{x})\quad \mu=0\\ & -\bar{\psi}\gamma^{\mu}\psi(-t,\bm{x})\quad \mu=1,2,3\\ \end{aligned}\right. \end{aligned}

  • ψˉγ5ψ\bar{\psi}\gamma^{5}\psi

Tψˉγ5ψT=(TψˉT)(γ5)∗(TψT)=ψˉ(γ3γ1)γ5(γ1γ3)ψ(−t,x)=ψˉγ5ψ(−t,x)\begin{aligned} T\bar{\psi}\gamma^{5}\psi T &= (T\bar{\psi}T)(\gamma^{5})^*(T\psi T)\\ &= \bar{\psi}(\gamma^3\gamma^1)\gamma^5(\gamma^1\gamma^3)\psi(-t,\bm{x})\\ &= \bar{\psi}\gamma^{5}\psi(-t,\bm{x})\\ \end{aligned}

  • ψˉγμγ5ψ\bar{\psi}\gamma^{\mu}\gamma^{5}\psi

Tψˉγμγ5ψT=(TψˉT)(γμγ5)∗(TψT)=ψˉ(γ3γ1)(γμ)∗γ5(γ1γ3)ψ(−t,x)={+ψˉγμγ5ψ(−t,x)μ=0−ψˉγμγ5ψ(−t,x)μ=1,2,3\begin{aligned} T\bar{\psi}\gamma^{\mu}\gamma^{5}\psi T &= (T\bar{\psi}T)(\gamma^{\mu}\gamma^{5})^*(T\psi T)\\ &= \bar{\psi}(\gamma^3\gamma^1)(\gamma^{\mu})^*\gamma^{5}(\gamma^1\gamma^3)\psi(-t,\bm{x})\\ &= \left\{\begin{aligned} & +\bar{\psi}\gamma^{\mu}\gamma^5\psi(-t,\bm{x})\quad \mu=0\\ & -\bar{\psi}\gamma^{\mu}\gamma^5\psi(-t,\bm{x})\quad \mu=1,2,3\\ \end{aligned}\right. \end{aligned}

电荷共轭

电荷共轭（charge conjugation） 描述了正反粒子间的变换，称为 CC 变换，可以用一个幺正算子表示。电荷共轭将一个给定自旋的粒子变换为相同自旋的反粒子。利用算子描述为：

CapsC=bpsCbpsC=aps(20)Ca_{\bm{p}}^sC = b_{\bm{p}}^s \quad Cb_{\bm{p}}^sC = a_{\bm{p}}^s \tag{20}

利用正反粒子的旋量表达式 (16)(16)，进行如下计算：

利用 p⋅σσ2=σ2p⋅σˉ∗\sqrt{p\cdot\sigma}\sigma^2 = \sigma^2\sqrt{p\cdot\bar{\sigma}^*}

(vs(p))∗=((p⋅σξ−s−p⋅σˉξ−s))∗=((−p⋅σiσ2(ξs)∗p⋅σˉiσ2(ξs)∗))∗=((−iσ2p⋅σˉ∗(ξs)∗iσ2p⋅σ∗(ξs)∗))∗=(−iσ2p⋅σˉξsiσ2p⋅σξs)=(0−iσ2iσ20)(p⋅σξsp⋅σˉξs)\begin{aligned} (v^s(p))^* &= (\begin{pmatrix} \sqrt{p\cdot\sigma}\xi^{-s}\\ -\sqrt{p\cdot\bar{\sigma}}\xi^{-s}\\ \end{pmatrix})^*\\ &=(\begin{pmatrix} -\sqrt{p\cdot\sigma}i\sigma^2(\xi^s)^*\\ \sqrt{p\cdot\bar{\sigma}}i\sigma^2(\xi^s)^*\\ \end{pmatrix})^*\\ &=(\begin{pmatrix} -i\sigma^2\sqrt{p\cdot\bar{\sigma}^*}(\xi^s)^*\\ i\sigma^2\sqrt{p\cdot \sigma^*}(\xi^s)^*\\ \end{pmatrix})^*\\ &=\begin{pmatrix} -i\sigma^2\sqrt{p\cdot\bar{\sigma}}\xi^s\\ i\sigma^2\sqrt{p\cdot \sigma}\xi^s\\ \end{pmatrix}\\ &=\begin{pmatrix} 0 & -i\sigma^2\\ i\sigma^2 & 0\\ \end{pmatrix} \begin{pmatrix} \sqrt{p\cdot\sigma}\xi^s\\ \sqrt{p\cdot \bar{\sigma}}\xi^s\\ \end{pmatrix}\\ \end{aligned}

可得：

us(p)=−iγ2(vs(p))∗vs(p)=−iγ2(us(p))∗(21)u^s(p) = -i\gamma^2(v^s(p))^* \quad v^s(p) = -i\gamma^2(u^s(p))^* \tag{21}

那么波函数在电荷共轭下的表示：

Cψ(x)C=∫d3p(2π)312Ep∑sC(apsus(p)e−ipx+bps†vs(p)eipx)C=∫d3p(2π)312Ep∑s(bps(−iγ2(vs(p))∗)e−ipx+aps†(−iγ2(us(p))∗)eipx)=−iγ2ψ∗(x)=−iγ2(ψ†)T=−i(ψˉγ0γ2)T\begin{aligned} C\psi(x)C &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s C(a_{\bm{p}}^{s} u^s(p)e^{-ipx}+b_{\bm{p}}^{s\dagger}v^s(p)e^{ipx})C\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (b_{\bm{p}}^{s} (-i\gamma^2 (v^s(p))^*)e^{-ipx}+a_{\bm{p}}^{s\dagger}(-i\gamma^2(u^s(p))^*)e^{ipx})\\ & = -i\gamma^2 \psi^*(x) = -i\gamma^2(\psi^\dagger)^T = -i(\bar{\psi}\gamma^0\gamma^2)^T\\ \end{aligned}

我们接下来考虑 Dirac 双线性映射在电荷共轭下的表示。

  • ψˉ\bar{\psi}

Cψˉ(x)C=Cψ†Cγ0=(CψC)†γ0=(−iγ2ψ∗)†γ0=((−iγ2ψ)∗)†γ0=(−iγ2ψ)Tγ0=(−iγ0γ2ψ)T\begin{aligned} C\bar{\psi}(x)C &= C\psi^\dagger C\gamma^0\\ &= (C\psi C)^\dagger \gamma^0\\ &= (-i\gamma^2\psi^*)^\dagger \gamma^0\\ &= ((-i\gamma^2\psi)^*)^\dagger \gamma^0\\ &= (-i\gamma^2\psi)^T\gamma^0 = (-i\gamma^0\gamma^2\psi)^T\\ \end{aligned}

  • ψˉψ\bar{\psi}\psi

CψˉψC=(CψˉC)(CψC)=(−iγ0γ2ψ)T(−iψˉγ0γ2)T=−(ψˉγ0γ2γ0γ2ψ)T=(ψˉψ)T=ψˉψ\begin{aligned} C\bar{\psi}\psi C&= (C\bar{\psi}C)(C\psi C)\\ &= (-i\gamma^0\gamma^2\psi)^T(-i\bar{\psi}\gamma^0\gamma^2)^T\\ &= -(\bar{\psi}\gamma^0\gamma^2\gamma^0\gamma^2\psi)^T\\ &= (\bar{\psi}\psi)^T = \bar{\psi}\psi\\ \end{aligned}

  • ψˉγμψ\bar{\psi}\gamma^{\mu}\psi

when μ≠0 and 2,(γμ)T=−γμCψˉγμψC=(CψˉC)γμ(CψC)=−(γ0γ2ψ)Tγμ(ψˉγ0γ2)T=(ψˉγ0γ2γμγ0γ2ψ)T=(ψˉγμγ0γ2γ0γ2ψ)T=−(ψˉγμψ)T=−ψˉγμψwhen μ=0 or 2,(γμ)T=γμCψˉγμψC=(CψˉC)γμ(CψC)=−(γ0γ2ψ)Tγμ(ψˉγ0γ2)T=−(ψˉγ0γ2γμγ0γ2ψ)T=(ψˉγμγ0γ2γ0γ2ψ)T=−(ψˉγμψ)T=−ψˉγμψ\begin{aligned} when\ \mu \neq 0 \ and\ 2 &,\quad (\gamma^{\mu})^T = -\gamma^{\mu}\\ C\bar{\psi}\gamma^{\mu}\psi C &= (C\bar{\psi}C)\gamma^{\mu}(C \psi C)\\ &= -(\gamma^0\gamma^2\psi)^T\gamma^{\mu}(\bar{\psi}\gamma^0\gamma^2)^T\\ &= (\bar{\psi}\gamma^0\gamma^2\gamma^{\mu}\gamma^0\gamma^2\psi)^T\\ &= (\bar{\psi}\gamma^{\mu}\gamma^0\gamma^2\gamma^0\gamma^2\psi)^T\\ &= -(\bar{\psi}\gamma^{\mu}\psi)^T = -\bar{\psi}\gamma^{\mu}\psi\\ when\ \mu = 0 \ or\ 2 &,\quad (\gamma^{\mu})^T = \gamma^{\mu}\\ C\bar{\psi}\gamma^{\mu}\psi C &= (C\bar{\psi}C)\gamma^{\mu}(C \psi C)\\ &= -(\gamma^0\gamma^2\psi)^T\gamma^{\mu}(\bar{\psi}\gamma^0\gamma^2)^T\\ &= -(\bar{\psi}\gamma^0\gamma^2\gamma^{\mu}\gamma^0\gamma^2\psi)^T\\ &= (\bar{\psi}\gamma^{\mu}\gamma^0\gamma^2\gamma^0\gamma^2\psi)^T\\ &= -(\bar{\psi}\gamma^{\mu}\psi)^T = -\bar{\psi}\gamma^{\mu}\psi\\ \end{aligned}

  • ψˉγ5ψ\bar{\psi}\gamma^{5}\psi

Cψˉγ5ψC=(CψˉC)γ5(CψC)=−(γ0γ2ψ)Tγ5(ψˉγ0γ2)T=−(ψˉγ0γ2γ5γ0γ2ψ)T=−(ψˉγ5γ0γ2γ0γ2ψ)T=(ψˉγ5ψ)T=ψˉγ5ψ\begin{aligned} C\bar{\psi}\gamma^{5}\psi C &= (C\bar{\psi}C)\gamma^{5}(C\psi C)\\ &= -(\gamma^0\gamma^2\psi)^T\gamma^5(\bar{\psi}\gamma^0\gamma^2)^T\\ &= -(\bar{\psi}\gamma^0\gamma^2\gamma^5\gamma^0\gamma^2\psi)^T\\ &= -(\bar{\psi}\gamma^5\gamma^0\gamma^2\gamma^0\gamma^2\psi)^T\\ &= (\bar{\psi}\gamma^5\psi)^T = \bar{\psi}\gamma^{5}\psi\\ \end{aligned}

  • ψˉγμγ5ψ\bar{\psi}\gamma^{\mu}\gamma^5\psi

when μ≠0 and 2,(γμ)T=−γμCψˉγμγ5ψC=(CψˉC)γμγ5(CψC)=−(γ0γ2ψ)Tγμγ5(ψˉγ0γ2)T=(ψˉγ0γ2γ5γμγ0γ2ψ)T=−(ψˉγμγ5γ0γ2γ0γ2ψ)T=(ψˉγμγ5ψ)T=ψˉγμγ5ψwhen μ=0 or 2,(γμ)T=γμCψˉγμψC=(CψˉC)γμγ5(CψC)=−(γ0γ2ψ)Tγμγ5(ψˉγ0γ2)T=−(ψˉγ0γ2γ5γμγ0γ2ψ)T=−(ψˉγμγ5γ0γ2γ0γ2ψ)T=(ψˉγμγ5ψ)T=ψˉγμγ5ψ\begin{aligned} when\ \mu \neq 0 \ and\ 2 &,\quad (\gamma^{\mu})^T = -\gamma^{\mu}\\ C\bar{\psi}\gamma^{\mu}\gamma^5\psi C &= (C\bar{\psi}C)\gamma^{\mu}\gamma^5(C \psi C)\\ &= -(\gamma^0\gamma^2\psi)^T\gamma^{\mu}\gamma^5(\bar{\psi}\gamma^0\gamma^2)^T\\ &= (\bar{\psi}\gamma^0\gamma^2\gamma^5\gamma^{\mu}\gamma^0\gamma^2\psi)^T\\ &= -(\bar{\psi}\gamma^{\mu}\gamma^5\gamma^0\gamma^2\gamma^0\gamma^2\psi)^T\\ &= (\bar{\psi}\gamma^{\mu}\gamma^5\psi)^T = \bar{\psi}\gamma^{\mu}\gamma^5\psi\\ when\ \mu = 0 \ or\ 2 &,\quad (\gamma^{\mu})^T = \gamma^{\mu}\\ C\bar{\psi}\gamma^{\mu}\psi C &= (C\bar{\psi}C)\gamma^{\mu}\gamma^5(C \psi C)\\ &= -(\gamma^0\gamma^2\psi)^T\gamma^{\mu}\gamma^5(\bar{\psi}\gamma^0\gamma^2)^T\\ &= -(\bar{\psi}\gamma^0\gamma^2\gamma^5\gamma^{\mu}\gamma^0\gamma^2\psi)^T\\ &= -(\bar{\psi}\gamma^{\mu}\gamma^5\gamma^0\gamma^2\gamma^0\gamma^2\psi)^T\\ &= (\bar{\psi}\gamma^{\mu}\gamma^5\psi)^T = \bar{\psi}\gamma^{\mu}\gamma^5\psi\\ \end{aligned}

总结

我们现在对以上所介绍的宇称变换 PP，时间反演 TT，电荷共轭 CC，及其联合操作 CPTCPT 进行总结。结果列在下表中。

我们用 (−1)μ(-1)^{\mu} 符号简记：

(−1)μ≡{+1,μ=0−1,μ=1,2,3(-1)^{\mu} \equiv \left\{\begin{aligned} & +1,\mu = 0\\ & -1,\mu = 1,2,3\\ \end{aligned}\right.

变换 电荷 QQ 角动量 JJ 动量 PP ψˉψ\bar{\psi}\psi ψˉγ5ψ\bar{\psi}\gamma^5\psi ψˉγμψ\bar{\psi}\gamma^\mu\psi ψˉγμγ5ψ\bar{\psi}\gamma^{\mu}\gamma^5\psi ψˉσμνψ\bar{\psi}\sigma^{\mu\nu}\psi
PP +1+1 +1+1 −1-1 +1+1 −1-1 (−1)μ(-1)^{\mu} −(−1)μ-(-1)^{\mu} (−1)μ(−1)ν(-1)^{\mu}(-1)^{\nu}
TT +1+1 −1-1 −1-1 +1+1 +1+1 (−1)μ(-1)^{\mu} (−1)μ(-1)^{\mu} −(−1)μ(−1)ν-(-1)^{\mu}(-1)^{\nu}
CC −1-1 +1+1 +1+1 +1+1 +1+1 −1-1 +1+1 −1-1
CPTCPT −1-1 −1-1 +1+1 +1+1 −1-1 −1-1 −1-1 +1+1

参考资料

  1. The Quantum Theory of Fields, vol1, Steven Weinberg, Chapter2 Appendix A