核子是短程的相互作用力。通常,我们假定两个核子之间的作用跟近旁的其他核子无关,但是这种两体相互作用的假设在原子核内并不准确。从核内核子间的介子场论,可以预期核子间可能存在着和两体作用不同的三体、四体作用。然而,核子间还是以两体作用为主的,用两体作用也能够解释很多事情,因此我们只讨论两体相互作用。
对于核力的研究主要有两种途径:
用唯象方法,对氘核和核子-核子散射实验进行分析,了解核力可能的性质。
用量子场论的方法从根本上解释核力,例如介子场理论。其效果与唯象场基本符合。
核子间的耦合是很强的,因此从量子色动力学出发,定量描述核力是很困难的。我们这里这介绍一些很唯象的、经验性的理论。
氘核是一个中子一个质子组成的,只有一个束缚态,即基态。考虑氘核中两个核子之间的相互作用,核子之间只有核力作用。
考虑一个中子一个质子的两体问题,我们可以将整体运动与相对运动分开,其中相对运动是我们所关心的。核子-核子相互作用势能可以写作 V = V ( r , p , σ 1 , σ 2 ) V =V(\bm{r},\bm{p},\bm{\sigma}_1,\bm{\sigma}_2) V = V ( r , p , σ 1 , σ 2 )
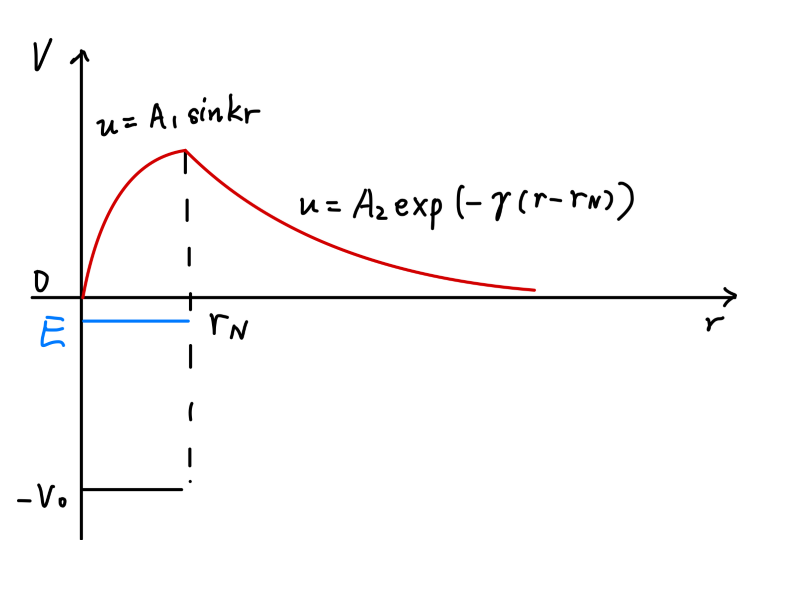
V ( r ) = { − V 0 r < r N 0 r > r N V(r)=
\left\{
\begin{aligned}
&- V_ 0 & r< r _N \\
& 0 &r > r_N \\
\end{aligned}
\right.
V ( r ) = { − V 0 0 r < r N r > r N
使用直角势阱来帮助我们了解核力的基本性质。
写出薛定谔方程:
[ − ℏ 2 2 μ ∇ 2 + V ( r ) ] ψ ( r ) = E ψ ( r ) [-\frac{\hbar^2}{2\mu }\nabla^2 + V(r)]\psi(\bm{r}) = E\psi(\bm{r})
[ − 2 μ ℏ 2 ∇ 2 + V ( r ) ] ψ ( r ) = E ψ ( r )
其中 μ \mu μ
μ = m n m p m n + m p ≈ 1 2 m p \mu = \frac{m_nm_p}{m_n+m_p} \approx \frac{1}{2}m_p
μ = m n + m p m n m p ≈ 2 1 m p
对于中心势场可以分离变量:
ψ ( r ) = u ( r ) r Y l m ( θ , φ ) \psi(\bm{r}) = \frac{u(r)}{r}Y_{lm}(\theta,\varphi)
ψ ( r ) = r u ( r ) Y l m ( θ , φ )
其中径向波函数 u ( r ) u(r) u ( r )
[ − ℏ 2 2 μ d d r 2 + l ( l + 1 ) ℏ 2 2 μ r 2 + V ( r ) ] u ( r ) = E u ( r ) [-\frac{\hbar^2}{2\mu}\frac{d}{dr^2} + \frac{l(l+1)\hbar^2}{2\mu r^2} + V(r) ] u(r) = Eu(r)
[ − 2 μ ℏ 2 d r 2 d + 2 μ r 2 l ( l + 1 ) ℏ 2 + V ( r ) ] u ( r ) = E u ( r )
基态对应 l = 0 l=0 l = 0
[ − ℏ 2 2 μ d d r 2 + V ( r ) ] u ( r ) = E u ( r ) [-\frac{\hbar^2}{2\mu}\frac{d}{dr^2} + V(r) ] u(r) = Eu(r)
[ − 2 μ ℏ 2 d r 2 d + V ( r ) ] u ( r ) = E u ( r )
解得:
u = { A 1 sin k r r < r N A 2 exp ( − γ ( r − r N ) ) r > r N u = \left\{
\begin{aligned}
&A_1\sin kr \quad & r < r_N\\
&A_2 \exp(-\gamma(r-r_N)) & r>r_N\\
\end{aligned}
\right.
u = { A 1 sin k r A 2 exp ( − γ ( r − r N ) ) r < r N r > r N
其中:
k = 2 μ ( V 0 − B ) ℏ , γ = 2 μ B ℏ k = \sqrt{\frac{2\mu(V_0-B)}{\hbar}},\quad \gamma = \frac{2\mu B}{\hbar}
k = ℏ 2 μ ( V 0 − B ) , γ = ℏ 2 μ B
由波函数的连续性条件(在 r = r N r=r_N r = r N
ctg [ 2 μ ( V 0 − B ) r N 2 ℏ 2 ] 1 2 = − [ B V 0 − B ] 1 2 \ctg [\frac{2\mu(V_0-B)r_N^2}{\hbar^2}]^{\frac{1}{2}} = -[\frac{B}{V_0-B}]^{\frac{1}{2}}
ctg [ ℏ 2 2 μ ( V 0 − B ) r N 2 ] 2 1 = − [ V 0 − B B ] 2 1
实验测量得到氘核束缚态结合能为 B = 2.22 M e V B = 2.22\mathrm{MeV} B = 2 . 2 2 M e V r N = 2.0 f m r_N=2.0\mathrm{fm} r N = 2 . 0 f m γ = V 0 − B B \gamma = \sqrt{\frac{V_0-B}{B}} γ = B V 0 − B
f ( γ ) = γ ctg ( a γ ) + 1 = 0 f(\gamma) = \gamma \ctg(a\gamma) + 1 =0
f ( γ ) = γ ctg ( a γ ) + 1 = 0
其中:
a = 2 μ B r N 2 ℏ 2 ≈ 0.463 a = \sqrt{\frac{2\mu Br_N^2}{\hbar^2}}\approx 0.463
a = ℏ 2 2 μ B r N 2 ≈ 0 . 4 6 3
由于氘核只有一个束缚态,可得 γ ≈ 3.930 \gamma \approx 3.930 γ ≈ 3 . 9 3 0
V 0 ≈ 36.6 M e V V_0 \approx 36.6 \mathrm{MeV}
V 0 ≈ 3 6 . 6 M e V
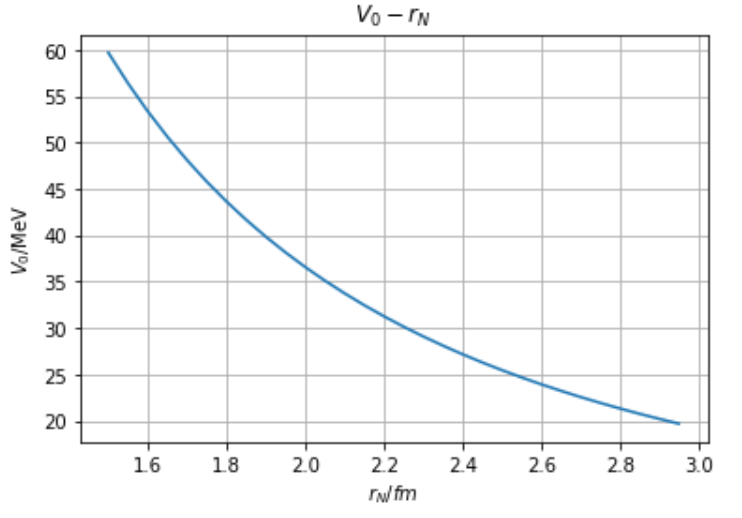
可以进一步计算 V 0 V_0 V 0 r N r_N r N
import numpy as npimport matplotlibimport matplotlib.pyplot as pltfrom scipy.optimize import fsolvee = 1.60217663410e-19 MeV = e*1e6 rn = np.arange(1.5 ,3.0 ,0.05 ) B = 2.225 *MeV mu = 1.6726219e-27 /2 hbar = 6.62607004e-34 /(2 *np.pi) a = np.sqrt(2 *mu*B)*rn/hbar V = [] for ai in a: func = lambda t : t/np.tan(ai*t*1e-15 )+1 result = fsolve(func,4 , xtol=1.49012e-08 ) gamma = result V0 = B*(gamma**2 +1 )/MeV V.append(V0[0 ]) fig, ax = plt.subplots() ax.plot(rn, V) ax.set (xlabel=r'$r_N/fm$' , ylabel=r'$V_0/\mathrm{MeV}$' ,title=r"$V_0-r_N$" ) ax.grid() plt.show()
得到结果如下:
我们发现,势阱深度将随着势阱变宽而逐渐减小。
利用连续性条件与归一化条件,就可以得到 A 1 , A 2 A_1,A_2 A 1 , A 2
现在对氘核的角动量做一些说明。氘核的总角动量有自旋角动量与轨道角动量两部分构成:
J = L + S \bm{J}=\bm{L}+\bm{S}
J = L + S
轨道角动量反应了核子之间的相对运动的轨道角动量。对于 l = 0 l=0 l = 0 3 S 1 \mathrm{^3S_1} 3 S 1 S S S 0 0 0 l = 1 l=1 l = 1 P P P l = 2 l=2 l = 2 D D D
实验测量得到氘核的总角动量为 J = 1 J = 1 J = 1 3 S 1 , 1 P 1 , 3 P 1 , 3 D 1 \mathrm{^3S_1}, \mathrm{^1P_1},\mathrm{^3P_1},\mathrm{^3D_1} 3 S 1 , 1 P 1 , 3 P 1 , 3 D 1 3 S 1 ( 96 % ) , 3 D 1 ( 4 % ) \mathrm{^3S_1}(96\%),\mathrm{^3D_1}(4\%) 3 S 1 ( 9 6 % ) , 3 D 1 ( 4 % )
非中心势的形式首先在 介子场论 中得到。介子场论首先由汤川秀树,他认为核子-核子间的相互作用是由于交换介子引起的,这里不过多介绍了,如果有机会,学习到以后的 QCD 后会介绍。我们现在对非中心势的形式不加证明的给出一些结果。
我们使用 σ 1 , σ 2 , r \bm{\sigma}_1,\bm{\sigma}_2,\bm{r} σ 1 , σ 2 , r
S 12 = 3 ( σ 1 ⋅ r ) ( σ 2 ⋅ r ) r 2 − σ 1 ⋅ σ 2 S_{12} = 3\frac{(\bm{\sigma}_1\cdot\bm{r})(\bm{\sigma}_2\cdot\bm{r})}{r^2} - \bm{\sigma}_1\cdot\bm{\sigma}_2
S 1 2 = 3 r 2 ( σ 1 ⋅ r ) ( σ 2 ⋅ r ) − σ 1 ⋅ σ 2
用 S = 1 2 ( σ 1 + σ 2 ) S = \frac{1}{2}(\bm{\sigma}_1+\bm{\sigma}_2) S = 2 1 ( σ 1 + σ 2 )
S 12 = 6 ( S ⋅ r ) 2 r 2 − 2 S 2 S_{12} = \frac{6(\bm{S}\cdot\bm{r})^2}{r^2}-2S^2
S 1 2 = r 2 6 ( S ⋅ r ) 2 − 2 S 2
非中心力通常是张量力(如果核力与动量无关,非中心力只有张量力),此时势函数可以写做以下形式:
V T = V T ( r ) S 12 V_{T} = V_{T}(r)S_{12}
V T = V T ( r ) S 1 2
我们发现:自旋单态无非中心力,三重态存在非中心力。
通过核子-核子散射实验可以探究核力的性质。对于低能核子散射,可以只考虑 S S S n \mathrm{n} n p \mathrm{p} p p \mathrm{p} p p \mathrm{p} p
从核子-核子散射实验中,可以获得核力主要性质为:
核力为短程力,有效力程小于 3 f m 3\mathrm{fm} 3 f m
核力与自旋有关,并且具有相当的交换力成分。
核力具有排斥芯,两核子的距离小于 0.4 f m 0.4\mathrm{fm} 0 . 4 f m
核力近似与电荷无关。
卢希庭 原子核物理
封面图 By Hydrogen-2.png: Joanjocderivative work: McSush (talk) - Hydrogen-2.png, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=8504303