Bloch 电子的动力学性质

准经典近似

布洛赫本征态可以表示为：

ψkn(r,t)=ei[k⋅r−En(k)ℏt]ukn(r)(1)\psi_{\bm{k}n}(\bm{r},t) = e^{i[\bm{k}\cdot \bm{r} - \frac{E_n(\bm{k})}{\hbar}t]}u_{\bm{k}n}(\bm{r}) \tag{1}

现在考虑使用 k\bm{k} 附近 Δk\Delta \bm{k} 范围内的布洛赫本征态叠加形成一个波包。

叠加得到：

ψkn(r,t)=1Δk∫k0−Δk2k0+Δk2ei[k⋅r−En(k)ℏt]ukn(r)dk≈ukn(r)Δkei[k0⋅r−En(k0)ℏt]∫−Δk2Δk2ei[δk⋅(r−[∇kEn(k)]k0ℏt)]dδk(2)\begin{aligned} \psi_{\bm{k}n}(\bm{r},t) &= \frac{1}{\Delta \bm{k}} \int_{\bm{k}_0 - \frac{\Delta \bm{k}}{2}}^{\bm{k}_0 + \frac{\Delta \bm{k}}{2}}e^{i[\bm{k}\cdot \bm{r} - \frac{E_n(\bm{k})}{\hbar}t]}u_{\bm{k}n}(\bm{r}) d\bm{k}\\ & \approx \frac{u_{\bm{k}n}(\bm{r})}{\Delta \bm{k}}e^{i[\bm{k}_0\cdot \bm{r} - \frac{E_n(\bm{k}_0)}{\hbar}t]} \int_{- \frac{\Delta \bm{k}}{2}}^{\frac{\Delta \bm{k}}{2}} e^{i[\delta\bm{k}\cdot (\bm{r} - \frac{[\nabla_{\bm{k}}E_n(\bm{k})]_{\bm{k}_0}}{\hbar}t)]} d\delta\bm{k}\\ \end{aligned}\tag{2}

对于积分号中的式子，令：

{ξ=x−1ℏ(∂En(k)∂kx)k0tη=y−1ℏ(∂En(k)∂ky)k0tζ=z−1ℏ(∂En(k)∂kz)k0t(3)\left\{ \begin{aligned} \xi & = x - \frac{1}{\hbar}(\frac{\partial E_n(\bm{k})}{\partial k_x})_{\bm{k}_0} t\\ \eta & = y - \frac{1}{\hbar}(\frac{\partial E_n(\bm{k})}{\partial k_y})_{\bm{k}_0} t\\ \zeta & = z - \frac{1}{\hbar}(\frac{\partial E_n(\bm{k})}{\partial k_z})_{\bm{k}_0} t\\ \end{aligned} \right.\tag{3}

结合 (3)(3)，可以给出 (2)(2) 式的最终结果为：

ψkn(r,t)≈ψk0n(r,t)sin⁡(Δkx2ξ)Δkx2ξsin⁡(Δky2η)Δky2ηsin⁡(Δkz2ζ)Δkz2ζ=ψk0n(r,t)A(r,t)(4)\begin{aligned} \psi_{\bm{k}n}(\bm{r},t) &\approx \psi_{\bm{k}_0n}(\bm{r},t) \frac{\sin (\frac{\Delta k_x}{2} \xi)}{\frac{\Delta k_x}{2} \xi}\frac{\sin (\frac{\Delta k_y}{2} \eta)}{\frac{\Delta k_y}{2} \eta}\frac{\sin (\frac{\Delta k_z}{2} \zeta)}{\frac{\Delta k_z}{2} \zeta}\\ & = \psi_{\bm{k}_0n}(\bm{r},t) A(\bm{r},t)\\ \end{aligned}\tag{4}

这表示一个 布洛赫波包。

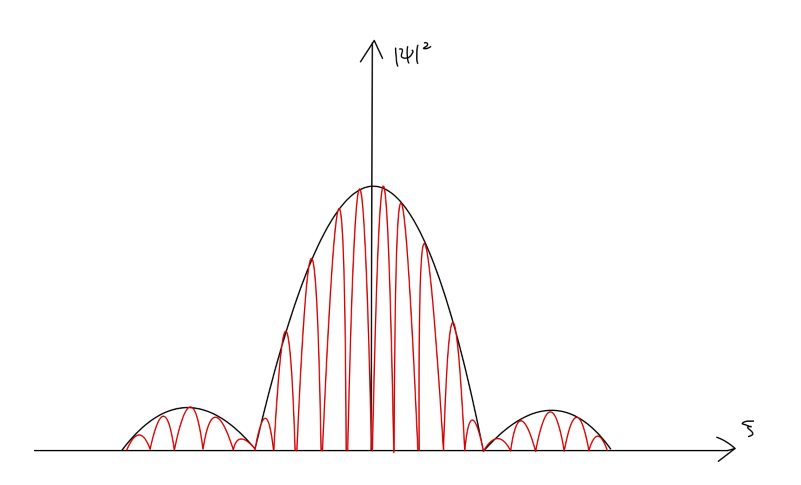
布洛赫波包

Fig：布洛赫波包

我们可以把波包的中心位置认为是一个经典粒子的位置：

{x=1ℏ(∂En(k)∂kx)k0ty=1ℏ(∂En(k)∂ky)k0tz=1ℏ(∂En(k)∂kz)k0t(5)\left\{ \begin{aligned} x &= \frac{1}{\hbar}(\frac{\partial E_n(\bm{k})}{\partial k_x})_{\bm{k}_0} t\\ y &= \frac{1}{\hbar}(\frac{\partial E_n(\bm{k})}{\partial k_y})_{\bm{k}_0} t\\ z &= \frac{1}{\hbar}(\frac{\partial E_n(\bm{k})}{\partial k_z})_{\bm{k}_0} t\\ \end{aligned} \right.\tag{5}

写成矢量形式为：

r=1ℏ∇En(k)k0t(6)\bm{r} = \frac{1}{\hbar} \nabla E_n(\bm{k})_{\bm{k}_0}t\tag{6}

得到速度为：

v=r˙=1ℏ∇En(k)k0(7)\bm{v} = \dot{\bm{r}} = \frac{1}{\hbar} \nabla E_n(\bm{k})_{\bm{k}_0}\tag{7}

即将波包的群速度看作 Bloch 电子的速度。

需要说明：Δk\Delta \bm{k} 的范围应远小于布里渊区的尺度：∣Δk∣≪2πa|\Delta \bm{k}|\ll \frac{2\pi}{a}
准经典近似成立的条件是：

  • 外场是时间和空间的缓变函数，外场变化的波长 λ≫a\lambda \gg a。
  • 频率 ℏω≪Eg\hbar\omega \ll E_g，以禁止带间跃迁。

在外力作用下 Bloch 电子状态的变化和准动量

考虑外力 F\bm{F} 的做功：

F⋅ds=F⋅vkdt\bm{F}\cdot d\bm{s} = \bm{F}\cdot\bm{v}_{\bm{k}}dt

能量改变:

dE(k)=∇E(k)⋅dkd E(\bm{k}) = \nabla E(\bm{k}) \cdot d\bm{k}

根据动能原理，有：

∇E(k)⋅dk=F⋅vkdt\nabla E(\bm{k}) \cdot d\bm{k} = \bm{F}\cdot\bm{v}_{\bm{k}}dt

考虑到：

vk=1ℏ∇kE(k)\bm{v}_{\bm{k}} = \frac{1}{\hbar}\nabla_{\bm{k}}E(\bm{k})

得到：

(ℏdkdt−F)⋅vk=0(\hbar \frac{d\bm{k}}{dt} - \bm{F})\cdot \bm{v}_{\bm{k}} = 0

对应有：

ddt(ℏk)−F=0(8)\frac{d}{dt}(\hbar\bm{k}) - \bm{F} = 0 \tag{8}

其中 ℏk\hbar\bm{k} 称为能带电子的准动量，为电子动量与晶格动量之和。其真实动量为 m∗vkm^*\bm{v}_{\bm{k}}。

加速度与有效质量

根据 (7)(7) 式，可以得到 Bloch 电子的加速度。

dvdt=1ℏddt[∇kE(k)]=1ℏ(dkdt⋅∇k)∇kE(k)=1ℏ2(F⋅∇k)∇kE(k)(9)\begin{aligned} \frac{d\bm{v}}{dt} &= \frac{1}{\hbar} \frac{d}{dt}[\nabla_{\bm{k}}E(\bm{k})]\\ &= \frac{1}{\hbar}(\frac{d\bm{k}}{dt}\cdot\nabla_{\bm{k}})\nabla_{\bm{k}}E(\bm{k})\\ &= \frac{1}{\hbar^2}(\bm{F}\cdot\nabla_{\bm{k}})\nabla_{\bm{k}}E(\bm{k})\\ \end{aligned}\tag{9}

写为分量形式：

dvαdt=∑β1ℏ2∂2E∂kα∂kβFβ(10)\frac{dv_{\alpha}}{dt} = \sum_{\beta}\frac{1}{\hbar^2} \frac{\partial^2 E}{\partial k_{\alpha}\partial k_{\beta}} F_{\beta}\tag{10}

写为矩阵形式：

(v˙xv˙yv˙z)=(1ℏ2∂2E∂kα∂kβ)3×3(FxFyFz)(11)\begin{pmatrix} \dot{v}_x\\ \dot{v}_y\\ \dot{v}_z\\ \end{pmatrix} = \begin{pmatrix} \frac{1}{\hbar^2}\frac{\partial^2 E}{\partial k_{\alpha}\partial k_{\beta}} \end{pmatrix}_{3\times 3} \begin{pmatrix} F_x\\ F_y\\ F_z\\ \end{pmatrix}\tag{11}

类比牛顿第二定律的形式，我们将速度项与“质量项”放在一边。

(FxFyFz)=(1ℏ2∂2E∂kα∂kβ)3×3−1(v˙xv˙yv˙z)=(mαβ∗)3×3(v˙xv˙yv˙z)(12)\begin{pmatrix} F_x\\ F_y\\ F_z\\ \end{pmatrix} = \begin{pmatrix} \frac{1}{\hbar^2}\frac{\partial^2 E}{\partial k_{\alpha}\partial k_{\beta}} \end{pmatrix}_{3\times 3}^{-1} \begin{pmatrix} \dot{v}_x\\ \dot{v}_y\\ \dot{v}_z\\ \end{pmatrix}= \begin{pmatrix} m^*_{\alpha\beta} \end{pmatrix}_{3\times 3} \begin{pmatrix} \dot{v}_x\\ \dot{v}_y\\ \dot{v}_z\\ \end{pmatrix}\tag{12}

{mαβ∗}\{m_{\alpha\beta}^*\} 称为 有效质量张量。

在主轴坐标系下有：

(mαβ∗)−1=1ℏ2(∂2E∂kx2000∂2E∂ky2000∂2E∂kz2)(m^*_{\alpha\beta})^{-1} = \frac{1}{\hbar^2}\begin{pmatrix} \frac{\partial^2 E}{\partial k_x^2} & 0 & 0\\ 0 & \frac{\partial^2 E}{\partial k_y^2} & 0\\ 0 & 0 & \frac{\partial^2 E}{\partial k_z^2}\\ \end{pmatrix}

有效质量是一个张量，一般情况下加速度的方向和外力方向不一致。只有在三个主轴方向时，外力与加速度方向一致，有效质量不同则速度方向大小不同，原因在于晶体的各项异性。

以简单立方 ss 带为例。由紧束缚近似得到：

E(k)=Es−J0−2J1(cos⁡kxa+cos⁡kya+cos⁡kza)E(\bm{k}) = E_s - J_0 - 2J_1(\cos k_xa + \cos k_ya + \cos k_za)

在带底，有 kx=ky=kz=0k_x = k_y = k_z = 0：

(mαβ∗)−1=1ℏ2(2a2J10002a2J10002a2J1)(m^*_{\alpha\beta})^{-1} = \frac{1}{\hbar^2}\begin{pmatrix} 2a^2J_1 & 0 & 0\\ 0 & 2a^2J_1 & 0\\ 0 & 0 & 2a^2J_1\\ \end{pmatrix}

在带顶，有 kx=ky=kz=±πak_x = k_y = k_z = \pm \frac{\pi}{a}

(mαβ∗)−1=1ℏ2(−2a2J1000−2a2J1000−2a2J1)(m^*_{\alpha\beta})^{-1} = \frac{1}{\hbar^2}\begin{pmatrix} -2a^2J_1 & 0 & 0\\ 0 & -2a^2J_1 & 0\\ 0 & 0 & -2a^2J_1\\ \end{pmatrix}

在鞍点，例如 XX 点 kx=ky=0,kz=πak_x = k_y = 0, k_z = \frac{\pi}{a}

(mαβ∗)−1=1ℏ2(2a2J10002a2J1000−2a2J1)(m^*_{\alpha\beta})^{-1} = \frac{1}{\hbar^2}\begin{pmatrix} 2a^2J_1 & 0 & 0\\ 0 & 2a^2J_1 & 0\\ 0 & 0 & -2a^2J_1\\ \end{pmatrix}

导体、绝缘体和半导体的能带

虽然固体中都包含有大量的电子，但有的具有很好的电子导电的性能，有的则基本上观察不到任何电子导电性。在能带论的基础上，首次对半导体、绝缘体、半导体的区分提出了理论上的说明[2]^{[2]}。

满带电子不导电

满带指一个能带上填充了 2N2N 个电子。

在同一能带中，k\bm{k} 态与 −k-\bm{k} 态具有相同的能量：

E(k)=E(−k)E(\bm{k}) = E(-\bm{k})

具有相反的速度：

v(k)=−v(−k)\bm{v}(\bm{k}) = -\bm{v}(-\bm{k})

在无外场时：

I=∑k−ev(k)=0I = \sum_{\bm{k}} -e\bm{v}(\bm{k}) = 0

现在说明：有外场时，仍然有 Itotal=0I_{total} = 0，满带电子不导电。

以一维能带为例。满带中，各个态都被电子充满。

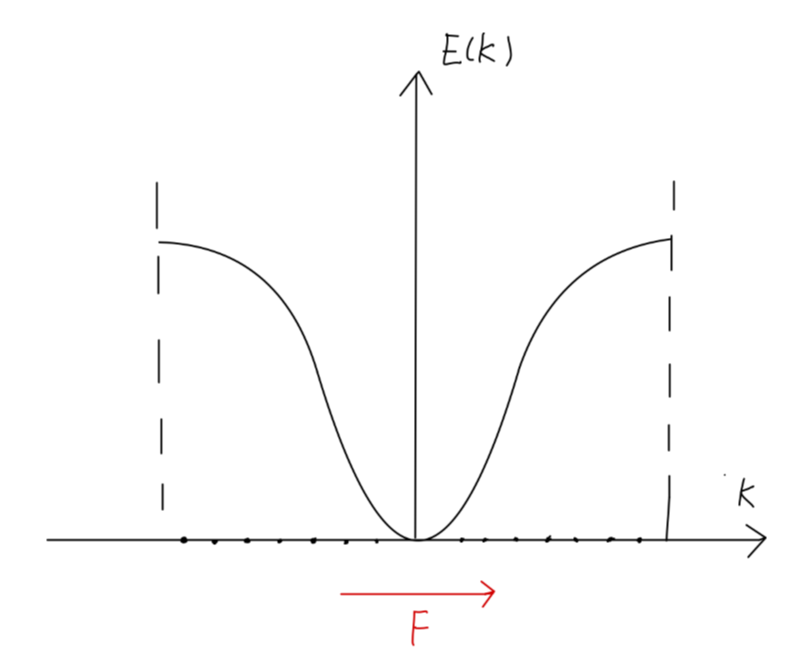
满带中的电子运动

Fig：满带中的电子运动

在电场 E\bm{E} 的作用下，电子受到的作用力为：

F=qE\bm{F} = q\bm{E}

那么所有电子所处的态都将以：

dkdt=Fℏ\frac{d\bm{k}}{dt} = \frac{\bm{F}}{\hbar}

的速度漂移。由于 k\bm{k} 为准动量，取值范围始终在第一布里渊区，那么从布里渊去边界出去的电子必定同时从另一个边界进入布里渊区。如此，在电场的作用下，能带的状态其实没有变化，因此不会产生电流。

未满带电子导电

对于未满带来说，无外场时，电子自发的填充在能量较低的态：总电流为零。

有外场时，电子在电场作用下产生漂移，原有的对称分布会被破坏。在不考虑晶格对电子的散射时，电子将持续进行漂移，形成一个周期性的电流，称为 k0\bm{k}_0 振荡（在实验上可以观察到）。若考虑晶格对电子的散射（电阻），电子将在电场的作用下形成一个稳定的、非对称的分布，产生一个恒定电流。

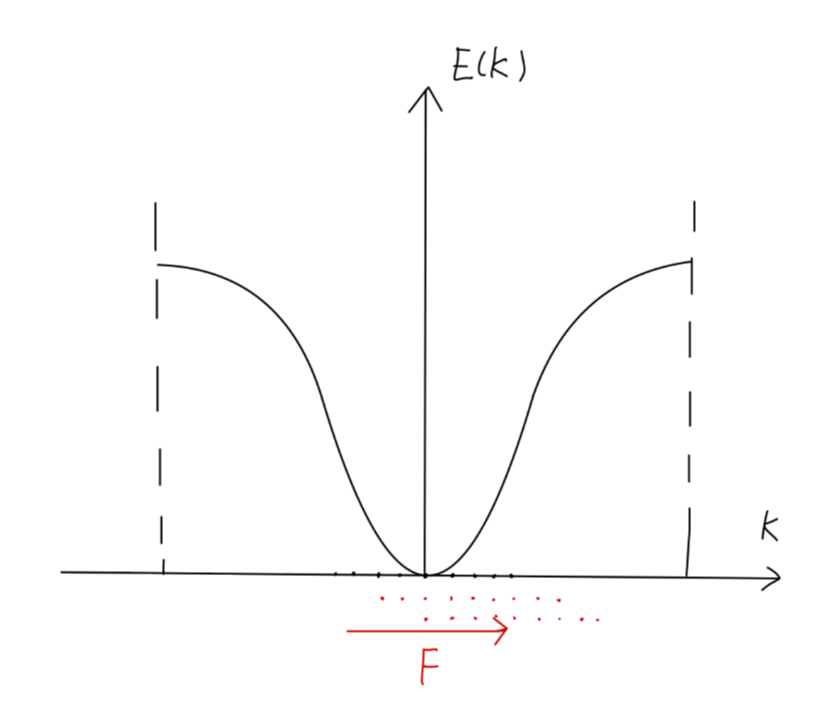
未满带中的电子运动

Fig：未满带中的电子运动

因此，未满带是可以导电的。

导体、绝缘体、半导体的能带特征

至此，基于能带论，我们可以对不同固体的导电性进行分类。

  • 导体：存在未满带
  • 绝缘体：只有满带或空带，禁带宽 5∼7eV5\sim7 eV
  • 半导体：只有满带或空带，禁带窄 ∼1eV\sim 1eV
  • 半金属：导带低和价带顶有交叠

对于半导体来说，在有限温度下，价带电子会激发到导带中去，这称为 本征激发。

我们将最高被填满的能带称为 价带，最低的未满带称为 导带。

一个有 NN 个元胞的固体每一个能带可容纳 2N2N 个电子：

  1. 每个初基胞中有奇数个价电子的固体：金属

  2. 每个初基胞中有偶数个价电子的固体：

    • 若有能带交叠：半金属
    • 若无能带交叠：
      • 宽禁带：绝缘体
      • 窄禁带：半导体

近满带和空穴

对于全满带来说：

∑k=0\sum \bm{k} = 0

对于近满带来说，考虑波矢为 ke\bm{k}_e 的轨道缺失一个电子，则系统的总波矢为 −ke-\bm{k}_e。近满带如同一个带正电荷的粒子，我们称这种准粒子称为 空穴。

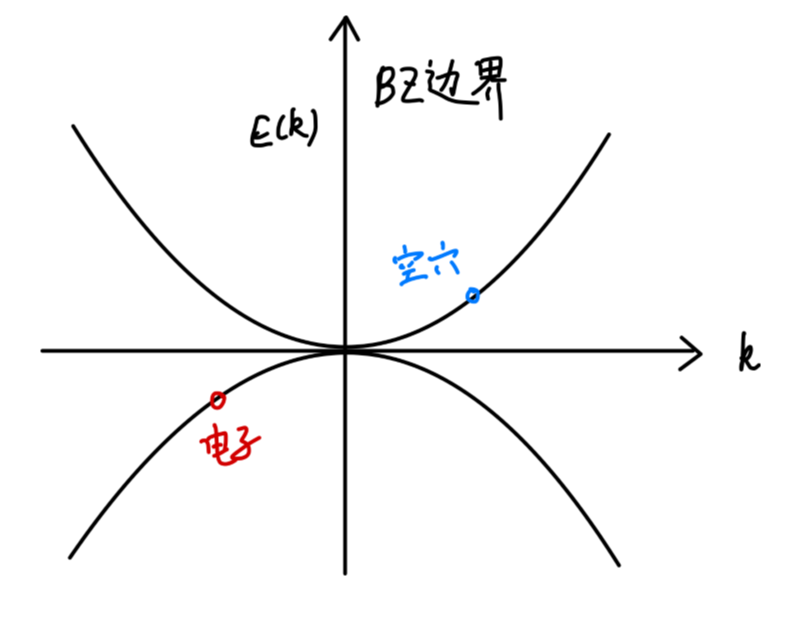
电子与空穴的能带

Fig：电子与空穴的能带

那么空穴的波矢为：

kh=−ke(13)\bm{k}_h= -\bm{k}_e \tag{13}

以价带带顶为能量零点，有：

Eh(kh)=−Ee(ke)(14)E_h(\bm{k}_h) = -E_e(\bm{k}_e) \tag{14}

空穴的速度等于缺失电子的速度：

vh(kh)=ve(ke)(15)\bm{v}_h(\bm{k}_{h}) = \bm{v}_e(\bm{k}_{e}) \tag{15}

有效质量符号相反：

me∗=−mh∗(16)m^*_{e} = -m^*_{h} \tag{16}

其他计算能带的方法

平面波法

基本函数、波函数、能谱

ψkn=eik⋅rukn,k∈1BZ\psi_{\bm{k}n} =e^{i\bm{k}\cdot\bm{r}} u_{\bm{k}n},\quad \bm{k}\in 1BZ

Bloch 波为正空间的周期函数。

ukn(r)=ukn(r+Rl),Rl=∑iliai(17)u_{\bm{k}n}(\bm{r}) = u_{\bm{k}n}(\bm{r}+\bm{R}_l),\quad \bm{R}_l = \sum_i l_i \bm{a}_i\tag{17}

由此可以按倒格矢展开，得到：

ukn(r)=1NΩ∑Khak(Kh)eiKh⋅r(18)u_{\bm{k}n}(\bm{r}) = \frac{1}{\sqrt{N\Omega}}\sum_{\bm{K}_h} a_{\bm{k}}(\bm{K}_h) e^{i\bm{K}_h\cdot\bm{r}}\tag{18}

得到：

ψkn(r)=1NΩ∑Khak(Kh)ei(k+Kh)⋅r(19)\psi_{\bm{k}n}(\bm{r}) = \frac{1}{\sqrt{N\Omega}}\sum_{\bm{K}_h} a_{\bm{k}}(\bm{K}_h) e^{i(\bm{k}+\bm{K}_h)\cdot\bm{r}}\tag{19}

其中 aka_{\bm{k}} 为倒空间的周期函数：

ak(Kh)=1NΩ∫ukn(r)e−iKh⋅rdr=1NΩ∫ψkn(r)ei(k+Kh)⋅rdr=1NΩ∫ψk+Kh,n(r)ei(k+Kh)⋅rdr=ak(k+Kh)\begin{aligned} a_{\bm{k}}(\bm{K}_h) &= \frac{1}{\sqrt{N\Omega}}\int u_{\bm{k}n}(\bm{r})e^{-i\bm{K}_h\cdot\bm{r}}d\bm{r}\\ &= \frac{1}{\sqrt{N\Omega}} \int \psi_{\bm{k}n}(\bm{r})e^{i(\bm{k}+\bm{K}_h)\cdot\bm{r}} d\bm{r}\\ &= \frac{1}{\sqrt{N\Omega}} \int \psi_{\bm{k}+\bm{K}_h,n}(\bm{r})e^{i(\bm{k}+\bm{K}_h)\cdot\bm{r}} d\bm{r}\\ &= a_{\bm{k}}(\bm{k}+\bm{K}_h) \end{aligned}

如此得到：

ψkn(r)=1NΩ∑Khak(k+Kh)ei(k+Kh)⋅r\psi_{\bm{k}n}(\bm{r}) = \frac{1}{\sqrt{N\Omega}}\sum_{\bm{K}_h} a_{\bm{k}}(\bm{k}+\bm{K}_h) e^{i(\bm{k}+\bm{K}_h)\cdot\bm{r}}

写为 Dirac 符号形式：

∣ψk⟩=∑Kha(k+Kh)∣k+Kh⟩(20)|\psi_{\bm{k}}\rangle = \sum_{\bm{K}_h}a(\bm{k}+\bm{K}_h) |\bm{k}+\bm{K}_h\rangle \tag{20}

考虑哈密顿量为：

H^=−ℏ22m∇2+V(r)=T^+V\hat{H} = -\frac{\hbar^2}{2m}\nabla^2 + V(\bm{r}) = \hat{T} + V

其中 V(r)=Vˉ+ΔVV(\bm{r}) = \bar{V} + \Delta V。Vˉ\bar{V} 为平均势，ΔV\Delta V 为周期势。

代入波动方程得到：

∑Kha(k+Kn)(T^+V−E)∣k+Kn⟩=0(21)\sum_{\bm{K}_h} a(\bm{k}+\bm{K}_n)(\hat{T} + V - E)|\bm{k}+\bm{K}_n\rangle = 0 \tag{21}

考虑到:

{⟨k+Km∣k+Kn⟩=δKn,KmT^∣k+Kn⟩=ℏ22m(k+Kn)2∣k+Kn⟩\left\{ \begin{aligned} &\langle \bm{k} + \bm{K}_m | \bm{k} + \bm{K}_n \rangle = \delta_{\bm{K}_n,\bm{K}_m}\\ & \hat{T}|\bm{k}+\bm{K}_n\rangle = \frac{\hbar^2}{2m} (\bm{k}+\bm{K}_n)^2 |\bm{k}+\bm{K}_n\rangle \end{aligned} \right.

求得：

∑Kn{[−ℏ22m(k+Kh)2−E(k)]δKn,Km+⟨k+Km∣V(r)∣k+Kn⟩}a(k+Kh)=0\sum_{\bm{K}_n} \{ [-\frac{\hbar^2}{2m}(\bm{k}+\bm{K}_h)^2 - E(\bm{k})]\delta_{\bm{K}_n,\bm{K}_m} + \langle \bm{k}+\bm{K}_m | V(\bm{r}) | \bm{k} + \bm{K}_n\rangle \} a(\bm{k}+\bm{K}_h) = 0

令：

⟨k+Km∣V(r)∣k+Kn⟩=1NΩ∫e−i(Kn−Km)⋅rV(r)dr=V(Kn−Km)\langle \bm{k} + \bm{K}_m | V(\bm{r}) | \bm{k} + \bm{K}_n\rangle = \frac{1}{N\Omega}\int e^{-i(\bm{K}_n-\bm{K}_m)\cdot\bm{r}} V(\bm{r})d\bm{r} = V(\bm{K}_n - \bm{K}_m)

其中 V(0)=0V(0)=0

得到：

[−ℏ22m∣k+Km∣2−E(k)]a(k+Km)+∑Kn≠Km′V(Kn−Km)a(k+Kn)=0[-\frac{\hbar^2}{2m}|\bm{k}+\bm{K}_m|^2 - E(\bm{k})] a(\bm{k}+\bm{K}_m) + \sum'_{\bm{K}_n\neq \bm{K}_m}V(\bm{K}_n-\bm{K}_m) a(\bm{k}+\bm{K}_n) = 0

有：

det⁡∣[−ℏ22m∣k+Km∣2−E(k)]δKn,Km+V(Kn−Km)∣=0(22)\det |[-\frac{\hbar^2}{2m}|\bm{k}+\bm{K}_m|^2 - E(\bm{k})] \delta_{\bm{K}_n,\bm{K}_m} + V(\bm{K}_n - \bm{K}_m)| = 0 \tag{22}

写为矩阵形式：

(ℏ22m(k+K1)2−E(k)V(K1−K2)V(K1−K3)⋯V(K2−K1)ℏ22m(k+K2)2−E(k)V(K2−K3)⋯⋮⋮⋮)\begin{pmatrix} \frac{\hbar^2}{2m}(\bm{k}+\bm{K}_1)^2 - E(\bm{k}) & V(\bm{K_1}-\bm{K}_2) & V(\bm{K_1}-\bm{K}_3) & \cdots \\ V(\bm{K_2}-\bm{K}_1) & \frac{\hbar^2}{2m}(\bm{k}+\bm{K}_2)^2 - E(\bm{k}) & V(\bm{K_2}-\bm{K}_3) & \cdots\\ \vdots & \vdots &\vdots & \\ \end{pmatrix}

其实我们可以注意到，平面波法与近自由电子近似有很多相似之处。从某种意义上来说，近自由电子近似就是只考虑能量相同的简并平面波的特殊平面波法。虽然平面波法看起来很美好，但其收敛性是很差的：这是由于波函数一般在离子实附近有振荡。为此，我们继续考虑 正交平面波法。

正交化平面波

Herring 在 1940 年提出了一种克服平面波法收敛差的方案。原则上，固体能带可以分为两类：

  • 内层电子 —— 窄带
  • 外层电子 —— 价带、导带

内层电子用 TBA 波函数描述：

∣ψC⟩=1N∑Rleik⋅Rl∣φCat(r−Rl)⟩|\psi_C\rangle = \frac{1}{\sqrt{N}} \sum_{\bm{R}_l} e^{i\bm{k}\cdot\bm{R}_l} | \varphi_C^{at}(\bm{r}-\bm{R}_l)\rangle

其满足的波动方程为：

H^∣ψC⟩=EC∣ψC⟩,⟨ψC′∣ψC⟩=δCC′\hat{H}|\psi_C\rangle = E_C|\psi_C\rangle, \langle \psi_{C'}|\psi_C\rangle = \delta_{CC'}

其中 C=1s,2s,2p,⋯C = 1s,2s,2p,\cdots。

对于外层电子，其在离子实区和离子实区外具有不同的性质。在离子实区外，电子受到很弱的势场作用，波函数很平滑，很像平面波。而在离子实区由于强烈的局域势作用，波函数急剧振荡。因此，我们选择使用平面波与内层电子波函数的线性组合来描述外层电子的波函数。这更符合实际的物理图像。

这就是说，我们考虑将波函数展开为：

∣ψk⟩=∑Kna(k+Kn)∣k+Kn⟩+∑CMβC∣ψC⟩(23)|\psi_{\bm{k}}\rangle = \sum_{\bm{K}_n} a(\bm{k}+\bm{K}_n)|\bm{k}+\bm{K}_n\rangle + \sum_{C}^M \beta_C |\psi_C\rangle\tag{23}

考虑到内层电子波函数 ∣ψC⟩|\psi_C\rangle 与 外层电子波函数 ∣ψk⟩|\psi_{\bm{k}}\rangle 只是同一个薛定谔方程不同本征值的解。它们应当是正交的。

考虑 正交化条件：

⟨ψC∣ψk⟩=0(24)\langle \psi_C|\psi_{\bm{k}}\rangle = 0 \tag{24}

如此得到：

βC=−∑Kna(k+Kn)⟨ψC∣k+Kn⟩(25)\beta_C = -\sum_{\bm{K}_n}a(\bm{k}+\bm{K}_n) \langle \psi_C | \bm{k}+\bm{K}_n\rangle \tag{25}

得到：

∣ψk⟩=∑Kna(k+Kn)(∣k+Kn⟩−∑C∣ψC⟩⟨ψC∣k+Kn⟩)=∑Kna(k+Kn)∣OPWk+Kn⟩\begin{aligned} |\psi_{\bm{k}}\rangle &= \sum_{\bm{K}_n} a(\bm{k}+\bm{K}_n)(|\bm{k}+\bm{K}_n\rangle - \sum_C |\psi_C\rangle\langle \psi_C | \bm{k} + \bm{K}_n\rangle)\\ &= \sum_{\bm{K}_n} a(\bm{k}+\bm{K}_n)|\mathrm{OPW}_{\bm{k}+\bm{K}_n}\rangle\\ \end{aligned}

其中 ∣OPW⟩|\mathrm{OPW}\rangle 为 正交化平面波（Orthogonalized Plane Wave）

∣OPWk⟩=∣k⟩−∑C∣ψC⟩⟨ψC∣k⟩|\mathrm{OPW}_{\bm{k}}\rangle = |\bm{k}\rangle - \sum_C |\psi_C\rangle\langle \psi_C|\bm{k}\rangle

代入波动方程：

(T^+V−E)∣ψk⟩=∑Ka(k+K)((T^+V−E)∣k+K⟩−(T^+V−E)∑C∣ψC⟩⟨ψC∣k+K⟩)=∑Ka(k+K)((ℏ2(k+K)22m+V−E)∣k+K⟩+∑C(E−EC)∣ψC⟩⟨ψC∣k+K⟩)=0\begin{aligned} (\hat{T} + V -E)|\psi_{\bm{k}}\rangle &= \sum_{\bm{K}} a(\bm{k}+\bm{K})((\hat{T} + V -E)|\bm{k}+\bm{K}\rangle - (\hat{T}+V-E)\sum_C |\psi_C\rangle\langle \psi_C|\bm{k}+\bm{K}\rangle)\\ & = \sum_{\bm{K}}a(\bm{k}+\bm{K})((\frac{\hbar^2(\bm{k}+\bm{K})^2}{2m} + V-E)|\bm{k}+\bm{K}\rangle + \sum_C (E-E_C) |\psi_C\rangle\langle \psi_C|\bm{k}+\bm{K}\rangle)\\ & = 0 \end{aligned}

由此可以得到决定能量本征值的久期方程：

det⁡∣(ℏ22m(k+K)2−E)δK,K′+⟨k+K′∣U∣k+K⟩∣=0(26)\det |(\frac{\hbar^2}{2m}(\bm{k}+\bm{K})^2-E)\delta_{\bm{K},\bm{K}'} + \langle \bm{k}+\bm{K}'|U|\bm{k}+\bm{K}\rangle| = 0 \tag{26}

其中矩阵元定义为：

⟨k+K′∣U∣k+K⟩=⟨k+K′∣V∣k+K⟩+∑C(E−EC)⟨k+K′∣ψC⟩⟨ψC∣k+K⟩\begin{aligned} \langle \bm{k}+\bm{K}'|U|\bm{k}+\bm{K}\rangle &= \langle \bm{k}+\bm{K}'|V|\bm{k}+\bm{K}\rangle + \sum_C(E-E_C) \langle \bm{k}+\bm{K}'|\psi_C\rangle\langle \psi_C|\bm{k}+\bm{K}\rangle \end{aligned}

方程 (26)(26) 在原则上也是无穷维的，但在实际计算中，只需要取很少几项就能达到很好的收敛性。

赝势方法

有关赝势方法可以参考 wiki。

赝势（pseudopotential），或有效势（effective potential），是指在对能带结构进行数值计算时所引入的一个虚拟的势。引入赝势有助于实现一个复杂的系统的近似计算。事实上，赝势近似法是正交平面波方法（OPW method）的延伸。

在赝势近似中，将原子的核电子（即非价电子）以及原子核共同产生的一个复杂的势置换成一个“有效势”（赝势）之后，薛定谔方程中的库仑势能项会变成一个有利于进行下一步计算的有效势能项。所构造的赝势通过替代原子中所有电子共同产生的势，简化了原子中心部分的态，从而可用包含较少节点的赝波函数来描述价电子[5]^{[5]}。

参考资料

  1. 胡安 章维益 固体物理学
  2. 黄昆 固体物理学
  3. 固体物理导论 C.Kittel
  4. 李正中 固体理论
  5. 维基百科编者. 赝势[G/OL]. 维基百科, 202120210519. https://zh.wikipedia.org/w/index.php?title=赝势&oldid=65691506.
    6 封面图 由Lorenzo Paulatto (Paulatz) - PWSCF, WanT and xCrysDen (w:Density functional theory)，CC BY-SA 3.0，https://commons.wikimedia.org/w/index.php?curid=1356155