广义相对论的数学基础（八）：拓扑空间

前面我们在集合中引入了代数结构，但很多情况下，这还不足以描述我们的物理对象。通常我们需要考虑一些“连续”的对象，需要考虑“邻近”等概念。但什么是连续？什么是邻近？这显然需要在集合上引入另外的结构。这种结构就是所谓的拓扑。有了拓扑，我们就可以研究邻域、连续性、连通性等概念。

拓扑

拓扑 (topology)
给定一个集合 $X$ ，它的一个子集系统 $\mathscr{U}$ 若满足：

包含空集 $\empty$ 和 $X$ 自身
$U$ 中有限个子集的交也属于 $\mathscr{U}$
$U$ 中任意多个子集的并也属于 $\mathscr{U}$

称 $\mathscr{U}$ 为 $X$ 的一个拓扑，二元组 $(X,\mathscr{U} )$ 称为 拓扑空间 ，通常可以简写为 $X$ 。 $\mathscr{U}$ 的子集称为这个拓扑空间的 开集（open sets）。

在集合上引入拓扑实质上就是在该集合上指定开集。

可以举出一些拓扑：
平庸拓扑
$\mathscr{U} = \{\empty,X\}$ 是 $X$ 的一个拓扑，称为平庸拓扑。
离散拓扑
$\mathscr{U} = 2^X$ 显然也是 $X$ 的一个拓扑，称为离散拓扑 (discrete)。

拓扑的粗细
设 $\mathscr{U}_1$ 和 $\mathscr{U}_2$ 是集合 $X$ 上的两个拓扑。若 $\mathscr{U}_1 \subset \mathscr{U}_2$ ，则称 $\mathscr{U}_1$ 比 $\mathscr{U}_2$ 粗。很显然，平庸拓扑最粗，离散拓扑最细。若同时有 $\mathscr{U}_1\subset \mathscr{U}_2,\mathscr{U}_2\subset \mathscr{U}_1$ ，则称这两个拓扑是 相当的（comparable）。

实数轴的通常拓扑
在实数集 $\mathbb{R}$ 中，所有开区间 $ a < x < b$ 的并，加上空集，形成一个拓扑。使得 $\mathbb{R}$ 成为一个拓扑空间。这个拓扑称为 $\mathbb{R}$ 上的通常拓扑。
单元素集合
单元素集合 $X = \{a\}$ 的拓扑只有 $1$ 个，即：

$\mathscr{U} = \{\empty,\{a\}\}$

它既是平庸拓扑又是离散拓扑
双元素集合
双元素集合 $X = \{a,b\}$ 的拓扑有 $4$ 个可能的拓扑，即：

$\begin{aligned} \mathscr{U}_1 &= \{\empty,\{a,b\}\}\\ \mathscr{U}_2 &= \{\empty,\{a,b\},\{a\}\}\\ \mathscr{U}_3 &= \{\empty,\{a,b\},\{b\}\}\\ \mathscr{U}_4 &= \{\empty,\{a,b\},\{a\},\{b\}\}\\ \end{aligned}$

拓扑的一些重要概念

闭集 (closed sets)
子集 $A \subset X$ 称为闭集，若 $X \setminus A$ 是开集。

例子，对于五元素集合 $X = \{a,b,c,d,e\}$ 的一个拓扑：

$\mathscr{U} = \{\empty,\{a,b,c,d,e\},\{a\},\{c,d\},\{a,c,d\},\{b,c,d,e \}\}$

对应的闭集为：

$\{a,b,c,d,e\},\empty,\{b,c,d,e\},\{a,b,e\},\{b,e\},\{a\}$

以下的概念我们也使用这个“五元素集合拓扑空间”举例说明。

不难得到，闭集对于有限交运算是封闭的。空集 $\empty$ 与全集既开又闭。

邻域 (neighborhood)
设 $x \in X$ ，点 $x$ 的邻域 $N(x)$ 是 $X$ 的一个子集，且包含了一个包含点 $x$ 的开集。类似的也可以定义某个子集的邻域。

例如在“五元素集合拓扑空间”中，开集 $\{a,b\}$ 是点 $a$ 的邻域，因为其包含了一个含有点 $a$ 的开集 $\{a\}$ ，而由于 $\{a,b\}$ 是 $X$ 的一个非开非闭集合，因此它是 $a$ 的非开非闭邻域。我们还可以得到： $\{a,c,d\}$ 是 $a$ 的开邻域； $\{a\}$ 是 $a$ 的既开又闭邻域； $\{a,b,e\}$ 是 $a$ 的闭邻域。

定理
子集 $A\subset X$ 是开集若它是它的每一点的邻域。

内点、外点和边界点（interior, exterior and boundary）

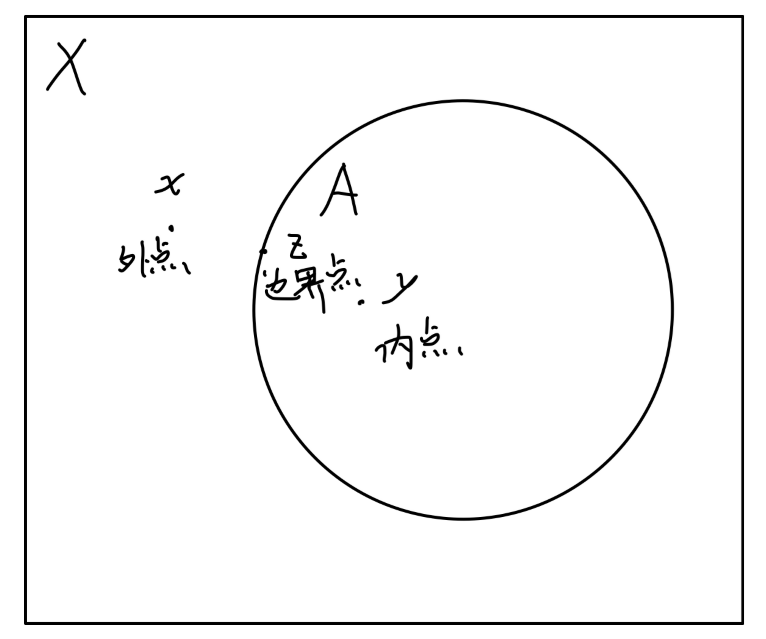
$x \in X$ 称为 $A \subset X$ 的内点，若存在一个开集 $U$ 使得 $x \in U \subset A$ 。子集 $A$ 所有内点形成的集合，记为 $\mathrm{Int} (A)$ ，并称为 $A$ 的 内部 (interior)。它是 $A$ 中最大的开集。
$x \in X$ 称为 $A \subset X$ 的外点，若其是 $A$ 的补集的内点。即 $x \in \mathrm{Int}(X\setminus A)$ 。所有外点的集合记为 $\mathrm{Ext}(A)$ 。
$x \in X$ 称为 $A \subset X$ 的 边界点，若它既不是内点也不是外点。 $A$ 的所有边界点形成的集合记为 $\dot{A}$ 。

在“五元素集合拓扑空间”中，令 $A = \{b,c,d\}$ ，可以得到内点为： $c,d$ ，由： $\mathrm{Int}A = \{c,d\}$ 。而 $X\setminus A = \{a,e\}$ ，有 $\mathrm{Int}(X\setminus A) = \{a\}$ ，故 $\mathrm{Ext}(A) = \{a\}$ ；边界点为 $b,e$ ，故有 $\dot{A} = \{b,e\}$ 。
我们直观的看到设 $A'$ 为含于 $A$ 的最大开集， $A''$ 为包含 $A$ 的最小闭集，那么有：

$\begin{aligned} \mathrm{Int}(A) &= A'\\ \mathrm{Ext}(A) &= X\setminus A''\\ \dot{A} &= A'' \setminus A'\\ \end{aligned}$

极限点 (limit point)
$x \in X$ 称为集合 $A \subset X$ 的极限点，如果 $x$ 的每一个邻域 $N(x)$ 至少包含一个不同于它自身的属于 $A$ 的点。即：

$(N(x) - {x}) \cap A\neq \empty ,\forall N(x)$

定理
极限点要么是内点，要么是边界点。

对于外点来说，能找到一个包含该点且含于 $X\setminus A$ 的开集合。

定理
若集合 $A\subset X$ 包含了它的所有极限点，则它是闭的。

容易得到它的补集将包含所有的外点，是一个开集合。

闭包 (closure)
$A$ 和它的所有极限点的并称为 $A$ 的闭包，记为 $\bar{A}$ 。

$\bar{A}$ 是包含 $A$ 的最小闭集。 $A$ 的闭包也是包含 $A$ 的所有闭集的交。

对于“五元素集合拓扑空间”来说，有：

$\begin{aligned} \overline{\{b,c,d\}} &= \{b,c,d,e\}\\ \overline{\{a\}} &= \{a\}\\ \overline{\{a,c\}} &= \{a,b,c,d,e\}\\ \end{aligned}$

稠密 (dense)
集合 $A$ 在 $X$ 中称为稠密，若 $\bar{A}= X$ 。

例如上述例子中，子集 $\{a,c\}$ 在 $\{a,b,c,d,e\}$ 中稠密。

可分性

可分性 (separation)
一个拓扑空间称为是 Hausdorff 的（ $T_2$ 可分的），若其中的任意两个不相同的点具有不相交的开邻域。

“五元素集合拓扑空间” 不是 Hausdorff 的，因为 $d,c$ 不满足 $T_2$ 可分要求。

我们遇到的情况都是 $T_2$ 可分的拓扑空间。若拓扑空间 $T_2$ 可分，则称其为 Hausdorff 空间。

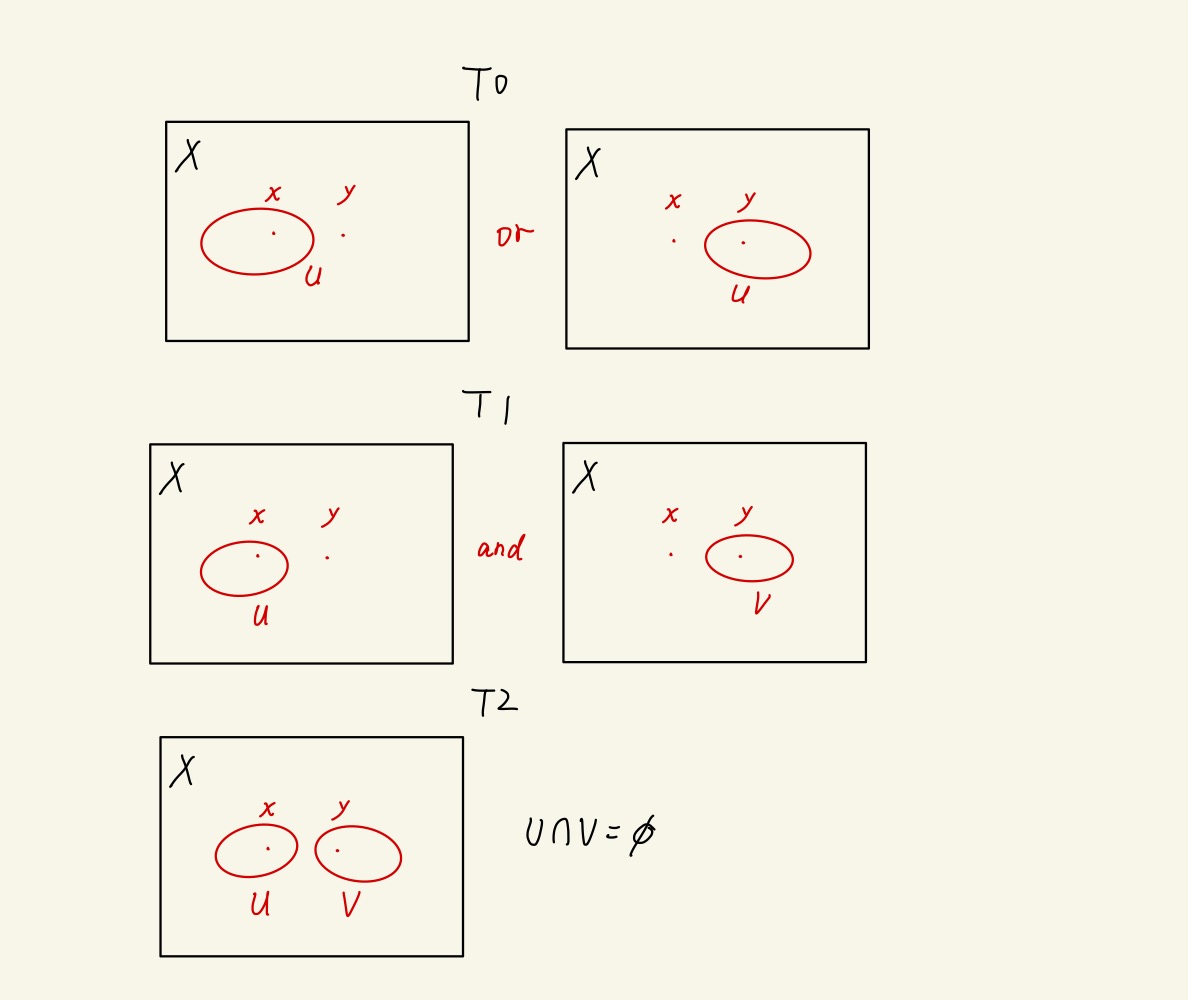
$T_0$ 可分
拓扑空间 $X$ 称为 $T_0$ 可分的，若对 $X$ 中的任意两点 $x$ 和 $y$ ，存在一个开集 $U$ 使得 $x \in U$ 而 $y \notin U$ ，或者 $y \in U$ 而 $x \notin U$ 。
$T_1$ 可分
拓扑空间 $X$ 称为 $T_1$ 可分的，若对 $X$ 中的任意两点 $x$ 和 $y$ ，存在开集 $U$ 和 $V$ 使得 $x \in U$ 而 $y \notin U$ ，以及 $y \in V$ 而 $x \notin V$ 。
$T_2$ 可分
拓扑空间 $X$ 称为 $T_2$ 可分的，若对 $X$ 中的任意两点 $x$ 和 $y$ ，存在两个不相交的开集 $U$ 和 $V$ 使得 $x \in U$ ，以及 $y \in V$ 。

紧致性

覆盖 (covering)
若集合 $X$ 一个子集系 $\{U _ i \}$ 满足 $\cup_ i U _ i \supseteq X$ ，则称这个子集系是 $X$ 的一个覆盖。若每个子集 $U_i$ 都是开集，则称这个覆盖为 开覆盖。

以后我们所说的覆盖都指开覆盖。

子覆盖 (subcovering)
将 $\{U _ i \}$ 中的子集抽出一部分形成一个子系统。若这个子系统也形成 $X$ 的一个覆盖，则称这个覆盖为 $\{U _ i \}$ 的子覆盖。

覆盖的细化 (refinement)
设拓扑空间 $X$ 有两个开覆盖 $\{U _ i \}$ 和 $\{V _ i \}$ ， $\{U _ i \}$ 称为 $\{V_ i \}$ 的细化，如果对于每一个 $ U_i$，存在一个 $V_j$ 使得 $U_i \subset V_ j$ 。