中心场定态问题
现在考虑相互作用势为中心势的情况,此时定态薛定谔方程为:
−2μℏ2∇2ψ(r)+V(r)ψ(r)=Eψ(r)(1)
在球坐标下,拉普拉斯算子可写为:
∇2=r21∂r∂(r2∂r∂)+r2sinθ1∂θ∂(sinθ∂θ∂)+r2sin2θ1∂φ2∂2(2)
此时波函数 ψ(r) 可以选取球坐标 r,θ,φ 为坐标:
ψ(r)=ψ(r,θ,φ)(3)
定态薛定谔方程写为:
−2μℏ2(r21∂r∂(r2∂r∂ψ)+r2sinθ1∂θ∂(sinθ∂θ∂ψ)+r2sin2θ1∂φ2∂2ψ)+V(r)ψ=Eψ
此时上述方程可以使用分离变量法求解:将波函数分为径向部分 R(r) 与角度部分 Y(θ,φ)。容易得到,角度部分的本征波函数就是球谐函数 Ylm(θ,φ),l=0,1,2,⋯,m=−l,−l+1,⋯,0,⋯,l−1,l。此时径向方程为:
−2μr2ℏ2drd(r2drdR)+(V(r)−r2l(l+1)ℏ2)R=ER(4)
对应的径向部分的本征波函数为 Rnl(r),于是本征波函数可写为:
ψnlm(r,θ,φ)=Rnl(r)Ylm(θ,φ)(5)
对于不同形式的中心势,Rnl 的形式不一样。上式中,n,l,m 分别称为 主量子数,角量子数,磁量子数。
对于氢原子波函数 ψnlm(r,θ,φ) 来说:主量子数决定了系统能量,角量子数决定角动量,磁量子数决定磁矩。
另外,对于方程 (4),可以令 χ(r)=rR(r),那么 (4) 成为:
−2μℏ2dr2d2χ(r)+[V(r)−r2l(l+1)ℏ2]χ(r)=Eχ(r)(6)
从形式上来说,径向波函数 χ(r) 满足的方程 (6) 可以看作如下的定态薛定谔方程:
H^rχ(r)=Eχ(r)(7)
其中:
H^r=2μp^2+V(r)−r2l(l+1)ℏ2(8)
其中的势能项为中心势加上离心势能项。
接下来我们针对特定中心势函数的定态问题进行讨论。
自由粒子球面波
首先是球面波,对应自由粒子在空间中的运动。此时 V(r)=0。方程 (6) 写为:
−2μℏ2dr2d2χ(r)−r2l(l+1)ℏ2χ(r)=Eχ(r)(9)
另外,球面波关于原点不随空间转动而变化,这决定了球面波的角度部分只能是 Y00。对应有 l=0,m=0。
方程 (9) 写为:
−2μℏ2dr2d2χ(r)=Eχ(r)(10)
考虑到在原点处 R(r) 应当为有限值,方程 (10) 给出的解为:
χ(r)=Asinkr,k=ℏ22μE
最终的波函数成为:
ψ(r)=ArsinkrY00(11)
一般情况下,对于任意 l,波函数的径向部分可以由球贝塞尔方程给出。这时波函数为:
ψ(r,θ,φ)=Akljl(kr)Ylm(θ,φ)(12)
利用连续参量下的球贝塞尔函数的归一化公式:
∫0∞jl(kr)jl(k′r)=2k2πδ(k−k′)=2μpπℏ3δ(E−E′)(13)
于是得到归一化后的波函数(归一化到 δ(E−E′))
ψklm(r,θ,φ)=ilπℏ32μpjl(kr)Ylm(θ,φ)(14)
这里添加的相因子 il 是为了之后时间反演运算的方便。
对于 l=0 的情况,称为 s 波;l=1 ,称为 p 波;l=2 ,称为 d 波,等等。
平面波具有特定的三个动量;这组波函数具有特定的角动量,角动量分量,能量。这两组解的集合都是完备的:任何波都可以由平面波或球面波叠加形成。
无限深球方势阱
无限深球方势阱的势能形式如下:
V(r)={0∞0<r⩽ar>a(15)
在 r=a 边界处,有边界条件:
ψ(a)=0(16)
在 0<r<a 时,其本征波函数就是 (14)。那么边界条件要求:
jl(ka)=0(17)
假定 jl 的第 n 个根为 αn(l)(n=1,2,⋯),那么能量本征值就可以确定了:
Enl=2μℏ2(kn(l))2=2μa2ℏ2(αn(l))2(18)
对应的径向波函数为:
Rnl(r)=Nnljl(kn(l)r)(19)
归一化系数由以下式子给出:
∫0∞Rnl2(r)r2dr=Nnl2∫0ajl2(kn(l)r)r2dr=Nnl22a3[−jl−1(αn(l))jl+1(αn(l))]=Nnl22a3[jl+1(αn(l))]2=1
于是得到归一化系数为:
Nnl=α3jl+12(αn(l))2(20)
于是无限深球方势阱的本征波函数可写为:
ψnlm(r,θ,φ)=α3jl+12(αn(l))2jl(kr)Ylm(θ,φ)(21)
有限球方势阱
有限球方势阱的形式如下:
V(r)={0V0r<ar>a(22)
分情况讨论:
径向方程成为:
⎩⎪⎪⎨⎪⎪⎧R′′+r2R′+[k2−r2l(l+1)]R=0R′′+r2R′+[(ik′)2−r2l(l+1)]R=0r<ar>a(23)
其中 k,k′ 由下式给出:
k=ℏ22mE,k′=ℏ22m(V−E)(24)
即可以得到 x<a 时,径向部分满足球贝塞尔方程;x>a 时,径向部分满足虚宗量贝塞尔方程。给出本征径向波函数为:
R(r)=⎩⎪⎪⎪⎨⎪⎪⎪⎧Akl2krπJl+21(kr)r<aBk′l2k′rπKl+21(k′r)r>a(25)
由 r=a 处波函数与一阶导数连续,得到决定能量的方程为:
∣∣∣∣∣2kaπJl+212kaπJl+21′∣r=a2k′aπKl+21(k′a)2k′aπKl+21(k′a)r=a′∣∣∣∣∣=0(26)
- E>V0(非束缚态):
此时系统的能量处处超过势垒。方程的解为:
{R(r)=Ajl(kr)R(r)=Bjl(k′r)+Cyl(k′r)r<ar>a(27)
在 r=a 处满足衔接条件:
{Ajl(ka)=Bjl(k′a)+Cyl(k′a)Ajl′(ka)=Bjl′(k′a)+Cyl′(k′a)(28)
得到的谱是连续的。
氢原子
考虑氢原子的原子核对电子的吸引势具有如下形式:
V(r)=−re2(29)
对应的本征波函数的形式如下:
ψnlm=Rnl(r)Ylm(θ,φ)(30)
其中径向波函数满足如下方程,作代换 χ=rR :
−2μℏ2χ′′+[−re2+2μr2l(l+1)ℏ2]χ=Eχ(31)
通过引入以下无量纲量:
a=μe2ℏ2=0.53A∘,E1=−2ℏ2μe4=−2ae2=−13.6eVε=E1E>0,ρ=2ε(ar)(32)
可以将 (31) 化为以下方程:
χ′′+[−41+ερ1−ρ2l(l+1)]χ=0(33)
考虑极限行为:
ρ→0,ρ→∞,χ→ρl+1χ→e−ρ/2(34)
考虑作如下代换:
χ=ρl+1e−ρ/2L(ρ)(35)
如此得到关于 L 的方程:
L′′+(ρ2l+2−1)L′−ρ1(l+1−ε1)L=0(36)
其解为合流超几何函数 F(l+1−ε1,2l+2,ρ)。我们在这里仍然使用级数写法。
采用如下级数解:
L=n=0∑∞anρn
得到递推关系:
(n+2l+2)(n+1)an+1=(n+l+1−ε1)an(37)
可以得到截断条件为:
ε1=nr+l+1=n=1,2,3,⋯
于是体系的能量为:
En=n21E1=n21(−2ae2),n=1,2,⋯,l=0,1,⋯,n−1
对于给定的 l 值,m 共有 2l+1 个不同的取值。那么得到能级 En 的简并度为:
En=l=0∑n−1(2l+1)=n2
方程 (36) 的解就为勒让德多项式。由此,对于径向部分,我们不加说明的给出其解为:
Rnl(r)=Nnle−nar(na2r)lLn−l−12l+1(na2r)(38)
其中归一化系数 Nnl 为:
Nnl={(na2)32n[(n+l)!]3(n−l−1)!}21(39)
考虑角度部分的波函数为:
ψnlm=Rnl(r)Ylm(θ,φ)
现在考虑一些特定量子数的波函数。例如取 n=1,l=0,m=0。得到:
ψ100(r,θ,φ)=πa31exp(−ar)(40)
这就是氢原子基态的波函数。
n,m,l 的不同取值决定了电子的状态。
下图,截自wiki [3],展示了不同量子数对应的原子轨道。
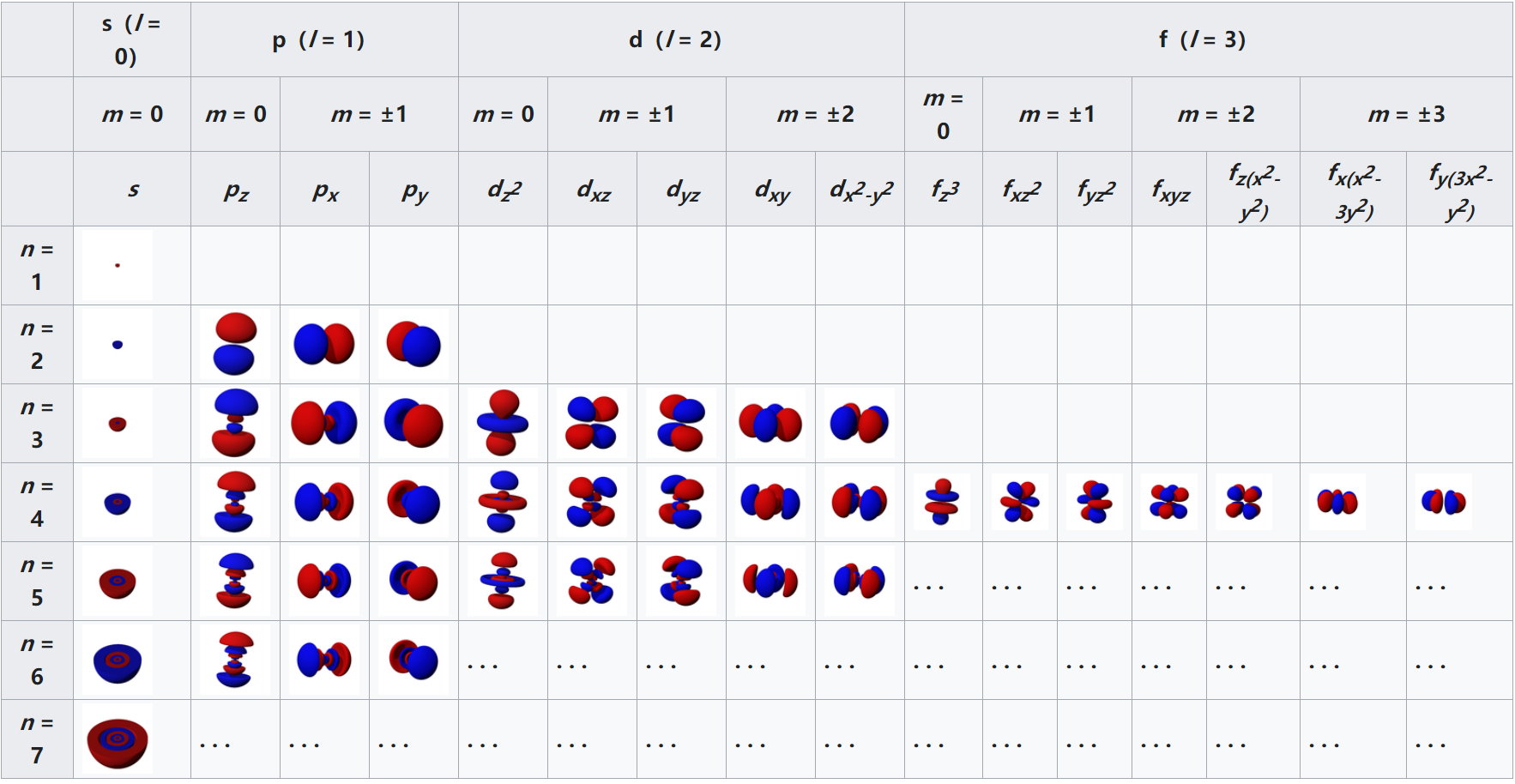
在以上的分析中,考虑到电子的质量比原子核的质量小很多,实际上在电子运动的过程中,原子核是几乎不动的,我们上述就默认原子核不动。若我们要精确求解电子运动,或者对于一些体系:如质子与 τ 子组成的原子,考虑原子核的运动是不可缺少的。
这成为一个两体问题。具体来说,体系的哈密顿量为:
H=2μ1p12+2μ2p22+V(∣x1−x2∣)(41)
通过以下代换:
R=μ1+μ2μ1x1+μ2x2,r=x1−x2(42)
可以将质心运动与相对运动分离开来:
H=2(μ1+μ2)pR2+2μpr2+V(r)(43)
其中 μ 为约化质量,有:
μ=μ1+μ2μ1μ2
对应的波函数也是可分离的,对应的相对部分就是之前的讨论。不同的是,需要将电子质量换为约化质量,这一点与经典力学中二体运动的结果也是一致的。对于整体运动部分,有:
HRψR(r)=ERψR(r)(44)
得到 (44) 的解是容易的。
参考资料
- 张永德 量子力学讲义
- 沈瑞 量子力学课件
- 原子轨道. (2021, February 8). Retrieved from 维基百科, 自由的百科全书: https://zh.wikipedia.org/w/index.php?title=原子轨道&oldid=64178768











