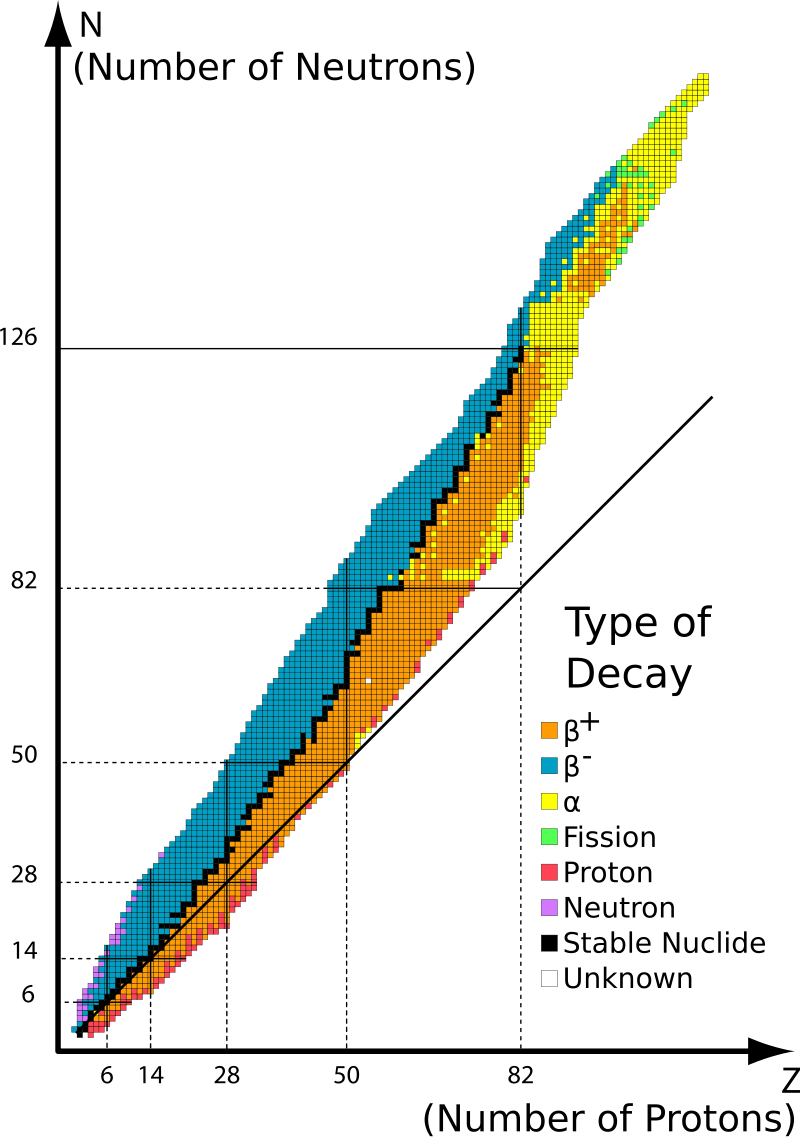前言：本组笔记为博主大三下学期原子核物理的课程笔记，上课采用的教材为卢希庭教授的《原子核物理》。

原子核的结合能

实验发现，原子核的质量总是小于组成它的核子的质量和（质量亏损）。这意味这核子在结合的过程中会释放能量，对应的能量就是 原子核结合能 。以 24He\mathrm{^4_2He} 核为例，有：

Δm(4He)=(2mp+2mn)−m(4He)\Delta m(\mathrm{^4He}) = (2m_p+2m_n)-m(\mathrm{^4He})

在具体计算过程中，我们总使用原子的质量（M(Z,A)M(Z,A) 或 M(ZAX)M(\mathrm{^A_ZX})）来代替核素的质量，对应有：

M(Z,A)=m(Z,A)+Zme−Be(Z)M(Z,A) = m(Z,A) + Zm_e -B_e(Z)

其中 Be(Z)B_e(Z) 代表核外电子的结合能。

对于一般的核反应过程，我们可以计算 广义质量亏损（反应前后静质量的差）来判断核反应能否进行。
某些原子核质量数据表中，用 Δ(Z,A)≡M(Z,A)−A\Delta(Z,A)\equiv M(Z,A) - A 来表示质量过剩。

现在计算原子核结合能 B(Z,A)B(Z,A )

B(Z,A)=Zmp+(A−Z)mn−m[ZAX]=(Zmp+Zme)+(A−Z)mn−(m[ZAX]+Zme)=(ZmH+ZBc[H])+(A−Z)mn−(m[ZAX]+Zme)+Bc[X,atom])≈ZmH+(A−Z)mn−m[ZAXatom]\begin{aligned} B(Z,A ) & = Zm_p + (A-Z)m_n -m[ \mathrm{^A_ZX} ] \\ & = (Zm_p + Zm_e) + (A-Z)m_n - (m[ \mathrm{^A_Z X}]+Zm_e)\\ & = (Zm_H + ZB_c[H]) + (A-Z)m_n-(m[ \mathrm{^A_Z X}]+Zm_e)+B_c[X,atom])\\ & \approx Zm_H + (A-Z)m_n -m[\mathrm{^A_Z X atom}] \end{aligned}

定义 Δ(ZAX)≡m[ZAX]−A\Delta(\mathrm{^A_ZX})\equiv m[\mathrm{^A_ZX}]- A，由此结合能公式可重写为：

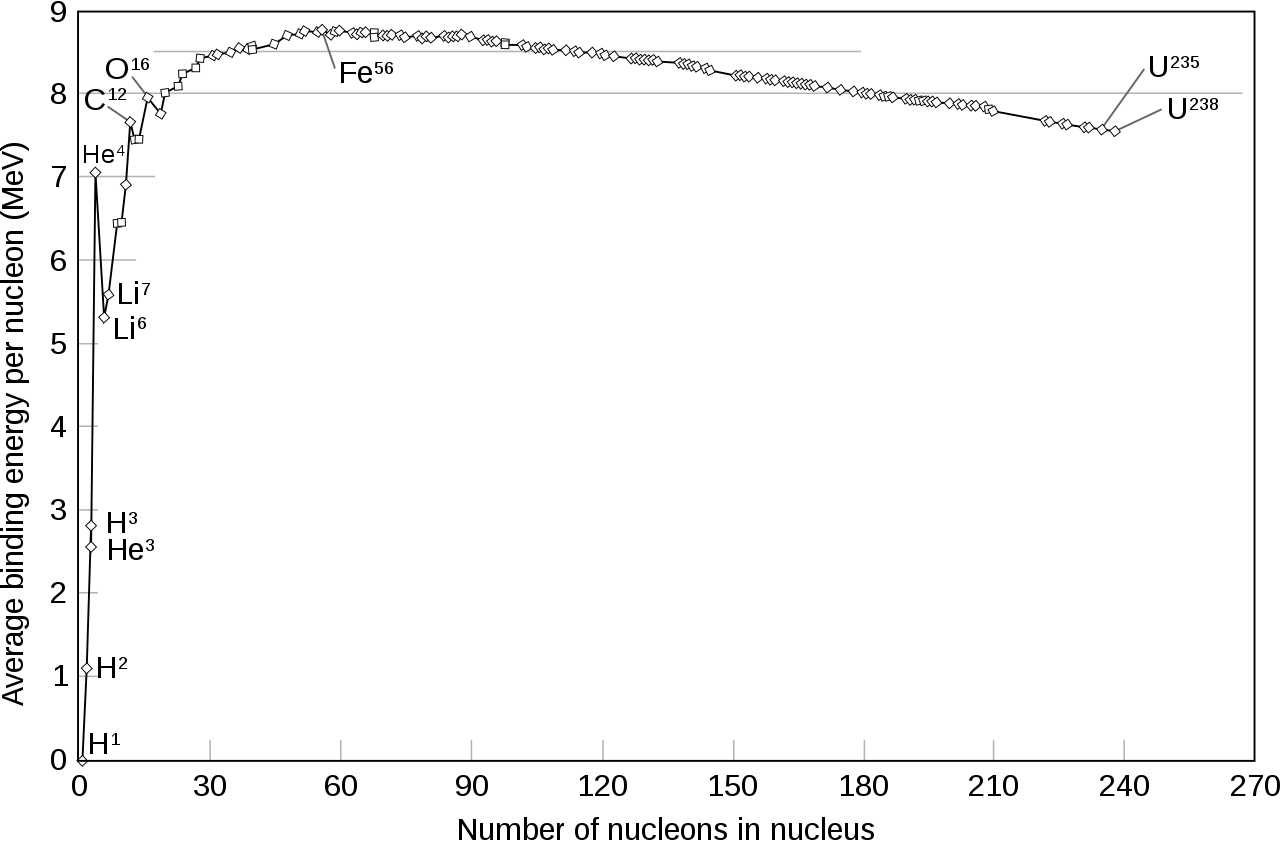
B(Z,A)=ZΔH+(A−Z)Δn−Δ(X)B(Z,A) = Z\Delta_{H}+(A-Z)\Delta_n - \Delta(\mathrm{X})

比结合能 定义为结合能与质量数的比值。比结合能反映了核素的稳定性。具体来说，比结合能越大，核素越稳定。一般认为，比结合能 B/AB/A 最大的是 56Fe\mathrm{^{56}Fe}。

大质量恒星演化中，内核发生核反应最后的产物就是 56Fe\mathrm{^{56}Fe}，不少观点认为是由于 56Fe\mathrm{^{56}Fe} 的比结合能是最大的。也有文献说明比结合能最大的其实是 62Ni\mathrm{^{62}Ni}，但恒星内部缺少从其他核素到 62Ni\mathrm{^{62}Ni} 的核反应路径。

ε=BA\varepsilon = \frac{B}{A}

最后一个核子的结合能
一个自由核子与原子核的剩余部分组成原子核时所释放的能量。Sn(Z,A),Sp(Z,A)S_n(Z,A),S_p(Z,A) 分表表示结合的核子是 质子 和是 中子 的情况。

原子核稳定性的经验规律

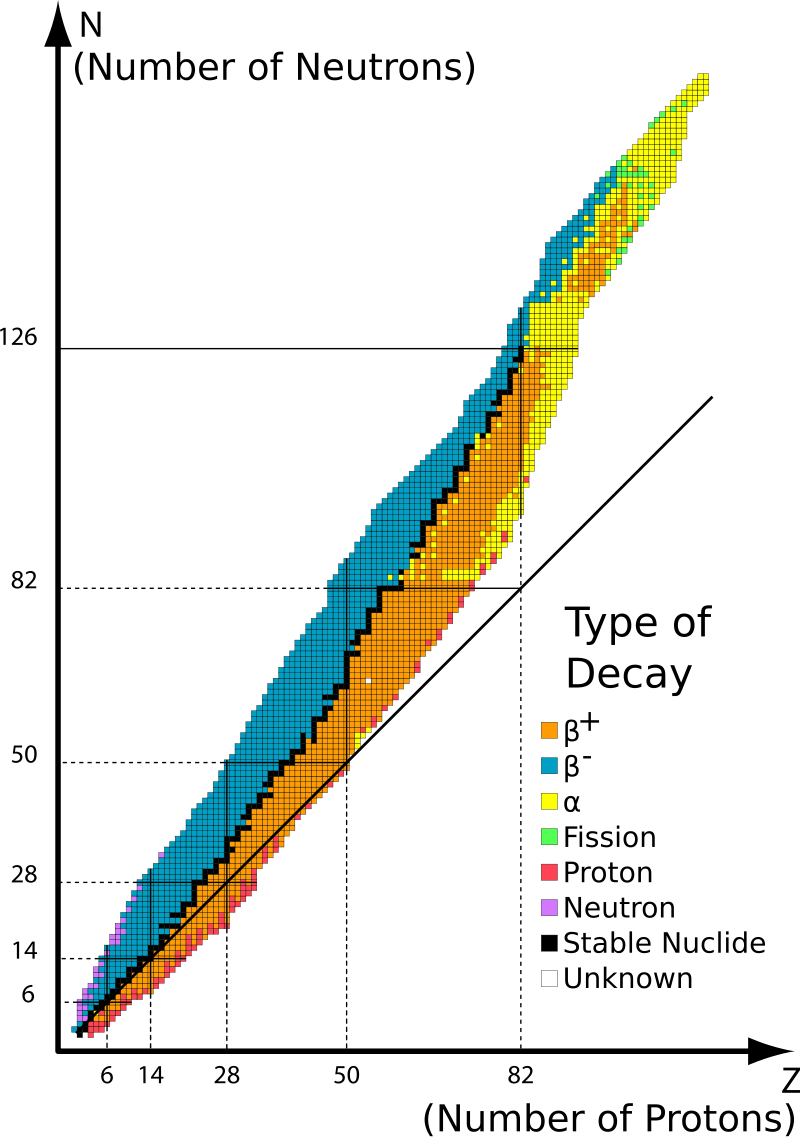
核素的稳定性[1]^{[1]}

自然界中有些原子核是稳定的，有些原子核会发生衰变。有关原子核的稳定性，我们得到了一些实验规律：

  • β\beta 稳定线
    我们将具有 β\beta 稳定性的核素绘制在 N−ZN-Z 平面内，在 β\beta 稳定线以上的核素是丰中子核，会发生 β−\beta^- 衰变； β\beta 稳定线以上的核素是丰中子核，会发生 β+\beta^+ 衰变或 EC。我们发现，在 A<40A<40 时，β\beta 稳定线近似成一条之间，且 Z/N≈1Z/N\approx 1，随着质量数增加，核素中质比大于1。
    β\beta 稳定线可以用以下经验公式表示：

Z=A1.98+0.0155A2/3Z = \frac{A}{1.98+0.0155 A^{2/3}}

  • 核子数的奇偶性
    对于稳定的核素，我们按照质子数 ZZ，中子数 NN 的奇偶性进行分类（odd/even）。
Z N 名称 稳定核素数目
e e 偶偶核 156
e o 偶奇核 48
o e 奇偶核 50
o o 奇奇核 5

我们发现，偶偶核的数目多于偶奇核、奇偶核，而奇奇核很少。这意味偶偶核更稳定，而大多数奇奇核不稳定。

  • 重核的不稳定性
    重核几乎都有 α\alpha 放射性。这是因为其比结合能较小，核子间结合较松。

原子核结合能的半经验公式

原子核的液滴模型
对原子核的研究常常采用唯象的模型法，即根据实验规律，类比熟知的物理对象，提出原子核结构或原子核反应机制的模型。实验发现：

  • 原子核的比结合能变化不大，由此核力应当具有饱和性。
  • 核密度几乎是常量，这意味这原子核是不可压缩的。

液滴模型 将原子核的上述性质同液体中相互作用力的饱和性、不可压缩性联系在一起。由此，类比液滴的能量，可以将原子核的结合能写做：

B=BV+BS+BcB = B_V + B_S + B_c

分别对应：

  • BVB_V：体积能。与体积（质量数）成正比：

BV=aVAB_V = a_VA

  • BSB_S：表面能。与表面积成正比：

BS=asA2/3B_S = a_sA^{2/3}

  • BcB_c：库伦能。

Bc=−acZ2A−1/3B_c = -a_c Z^2A^{-1/3}

考虑到质子的库伦自能：Z2→Z(Z−1)Z^2\rightarrow Z(Z-1)

除此之外，根据原子核稳定性的实验规律，需要考虑一些修正项。

  • BaB_{a}：对称能

大多数稳定的轻核质子数 ZZ 等于中子数 NN。对称能是一种量子效应，考虑到泡利不相容原理，在中子、质子对称相处的情形下，能够填充的单粒子能级更低。

Ba=aa(Z−A2)(N−A2)/A=−aa(A2−Z)2A−1\begin{aligned} B_{a} &= a_{a}(Z-\frac{A}{2})(N-\frac{A}{2})/A\\ & = -a_{a}(\frac{A}{2}-Z)^2A^{-1}\\ \end{aligned}

  • BpB_{p} 对能

基于实验：偶偶核稳定，偶奇、奇偶核较少，奇奇核很少。对能是一种量子效应，成对的中子或质子在接近时具有很强的相互吸引力，使得结合能升高。

Bp=δapA−1/2 B_{p} = \delta a_p A^{-1/2}

  • 偶偶核：δ=1\delta=1
  • 奇偶、偶奇核：δ=0\delta=0
  • 奇奇核：δ=−1\delta = -1

综合以上，我们得到 原子核结合能的半经验公式

B=aVA−aSA2/3−acZ2A−1/3−aa(A2−Z)2A−1+apδA−1/2B = a_VA - a_SA^{2/3}-a_cZ^2A^{-1/3}-a_{a}(\frac{A}{2}-Z)^2A^{-1}+a_p\delta A^{-1/2}

利用结合能模型对实验数据进行拟合，得到的一组参量是：

aV=15.835MeVaS=18.33MeVac=0.714MeVaa=92.80MeVap=11.2MeV\begin{aligned} &a_{V} = 15.835 \mathrm{MeV}\\ &a_{S} = 18.33 \mathrm{MeV}\\ &a_{c} = 0.714 \mathrm{MeV}\\ &a_{a} = 92.80 \mathrm{MeV}\\ &a_{p} = 11.2 \mathrm{MeV}\\ \end{aligned}

利用结合能公式，可以计算核素的质量（原子核）：

m(Z,A)=Zmp+(A−Z)mn−B(Z,A)m(Z,A) = Zm_p + (A-Z)m_n - B(Z,A)

原子质量：

M(Z,A)≈ZM(1H)+(A−Z)mn−B(Z,A)M(Z,A) \approx ZM(\mathrm{^1H}) + (A-Z)m_n - B(Z,A)

下面讲一个应用：对于上述得到的原子质量，若令 AA 不变，可以将 M(Z,A)M(Z,A) 当做关于 ZZ 的二次函数。这称为 同量异位素质能抛物线，利用它可以判断 β\beta 衰变稳定性。

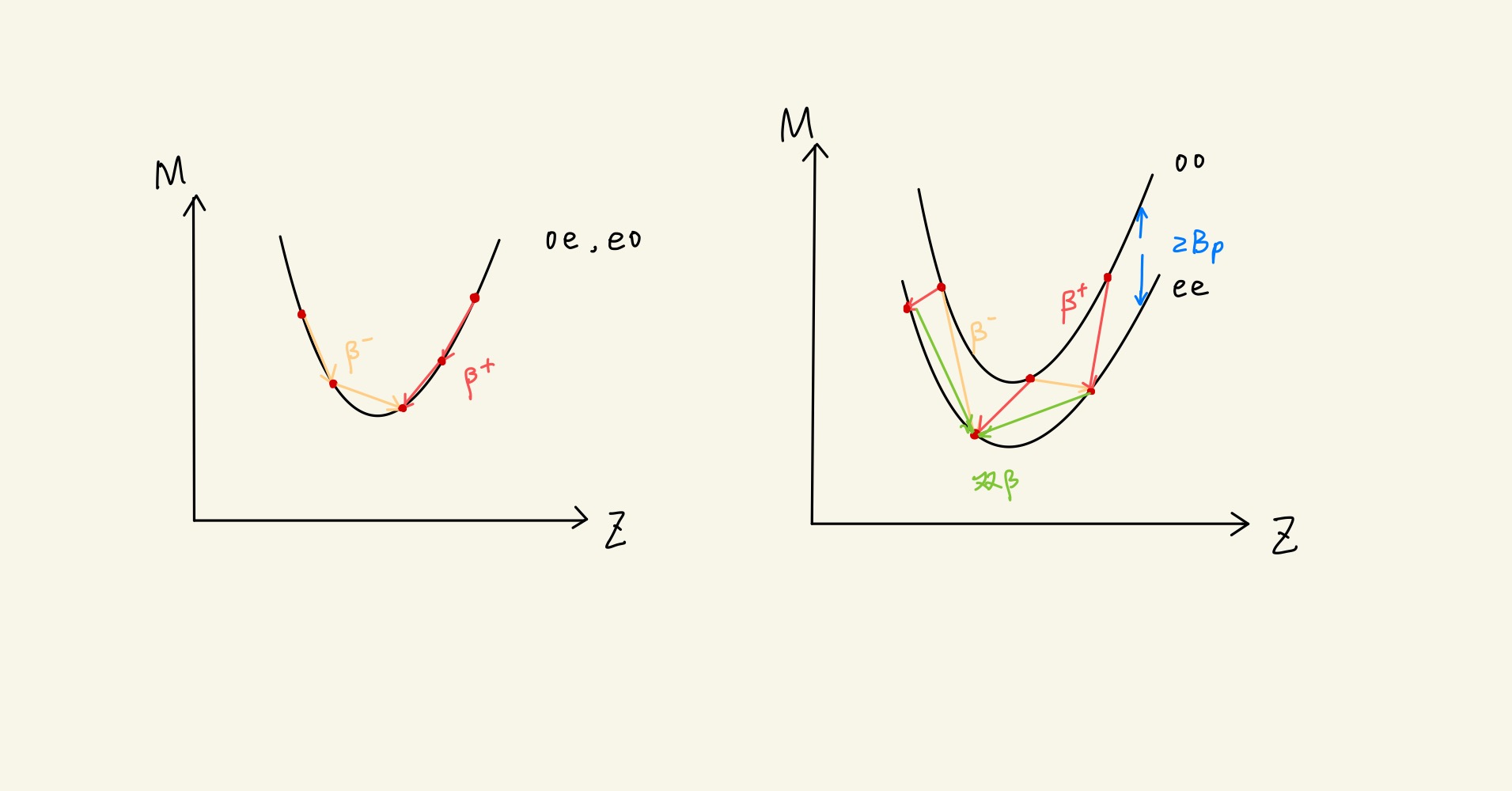
衰变总是向能量（质量）降低的反向进行。对于单 β\beta 衰变来说，奇偶核和偶奇核相互转换，对应左图情况；偶偶核和奇奇核相互转换，对应右图情况，注意这两条同量异位素质能抛物线相差两倍对能。

不难得到有关 β\beta 衰变稳定性的规律：

  • 奇奇核，发生 β,β+\beta,\beta^+ 衰变
  • 奇偶核
    • 发生 β+\beta^+ 衰变（Z>Z0Z > Z_0）
    • 发生 β−\beta^- 衰变（Z<Z0Z < Z_0）
  • 偶偶核，发生 双 β\beta 衰变

    同时转换两个核子

参考资料

  1. By Table_isotopes.svg: Napy1kenobiderivative work: Sjlegg (talk) - Table_isotopes.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=6703703
  2. 卢希庭 原子核物理
  3. 封面图 By Kjerish - Own workThis file has been extracted from another file: CNO Cycle.svg, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=54378478