广义相对论的数学基础（十一）：切空间

上一篇中我们提到了流形上的一些概念，我们先简单回顾一下：

对于一个流形上的点 $p$ ，给定一个坐标卡 $(U,\varphi)$ ，其中 $\varphi$ 是一个从坐标域 $U$ 到 $\mathbb{R}^n$ 中某个开集的同胚：

$\varphi: U\rightarrow \mathbb{R}^n$

它将流形上的点 $p$ 映成欧氏空间 $\mathbb{R}^n$ 中的点 $\varphi(p)$ ，那么在欧氏空间中 $\varphi(p)$ 可以用一组数表示：

$(x^1 (p),\cdots ,x^ n (p))$

这称为点 $p$ 在坐标卡 $(U,\varphi)$ 的坐标， $x^i$ 称为坐标函数：

$\begin{aligned} &x^i : \mathbb{R}^n \rightarrow \mathbb{R}\\ &u \mapsto x^i (u) = (u)^i ,\ \forall u \in \mathbb{R}^n \end{aligned}$

对于流形上的点 $p$ ，其在坐标卡 $(U,\varphi)$ 的坐标（第 $i$ 个分量）为：

$\begin{aligned} (\varphi(p))^i = x^i(\varphi(p)) = x^i\circ\varphi(p) = x^i_{\varphi}(p)\\ \end{aligned}$

流形上的曲线是如下映射：

$c: I\subset\mathbb{R} \rightarrow X$

在 $X$ 的坐标卡 $(U,\varphi)$ 下，该曲线可表示为：

$x ^ i = (\varphi \ \circ\ c(t))^ i ,\quad i = 1,\cdots ,n$

我们也常将上面的表达式简写为：

$x^i = c^i(t) \ or\ x^i = x^i(t)$

有了微分结构之后，我们可以在流形上构造出非常有用的一些几何对象。例如：所谓的切矢量、切空间、张量等等。但我们考虑到：

一般的微分流形不具备线性空间这样的代数结构。因此，给定一个一般的微分流形后，我们不可能像欧氏空间那样定义一个矢量。
欧几里德空间中曲线和曲面的切矢量，可以通过将一个微分流形嵌入高维的欧氏空间来定义切矢量。但这种定义依赖于微分流形的非内禀结构（需要将流形嵌入到一个高维的流形，如嵌入到高维的欧几里德空间）。例如一个对于一个二维流形，我们总可以将其嵌入到三维欧氏空间中，并定义相应的切矢量：

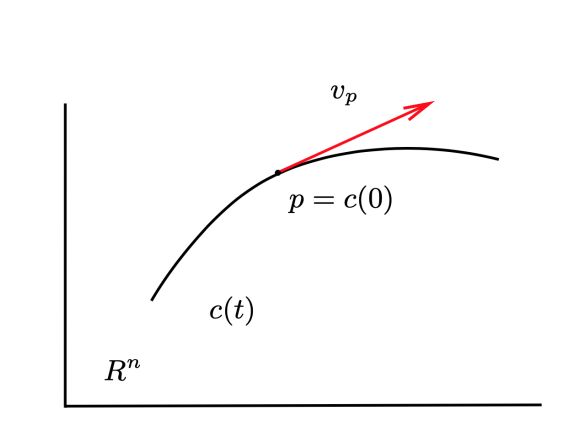
由此，我们希望有一个更为自然的关于切矢量的定义。

切空间

我们已经定义了流形上的可微函数形成的环 $\mathscr{F}(X)$ ，而且 $\mathscr{F}(X)$ 具有自然的 $\mathbb{R}$ 上的线性空间结构。流形上任意一点上的切矢量和切空间的定义与 $\mathscr{F}(X)$ 密切相关。

于是我们定义：流形 $X$ 上 $p$ 点的一个 切矢量 (tangent vector) $v_p$ 是 $\mathscr{F}(X)$ 上的线性函数

$\begin{aligned} &v_p(\lambda_1f_1 + \lambda_2f_2) = \lambda_1v_p(f_1) + \lambda_2v_p(f_2)\\ &\forall\ \lambda_1,\lambda_2\in \mathbb{R},\quad \forall\ f_1,f_2\in\mathscr{F}(X) \end{aligned}$

且满足 莱布尼茨法则 (Leibniz rule):

$v_p (f_ 1 f_ 2 ) = v_ p (f_ 1 )f_ 2 + f_ 1 v_ p (f_ 2 )$

满足莱布尼茨法则的线性函数是一种 导数算子 (derivative operator)。 $v_p (f)$ 可以理解为 $f \in \mathscr{F}(X)$ 沿着 $v_ p$ 的方向导数。

通常我们将 $p$ 点所有切矢量的集合记为 $T_p X$ 。容易在 $T_p X$ 定义加法和数乘使 $T_p X$ 形成一个线性空间，称为 切空间 (tangent space)。

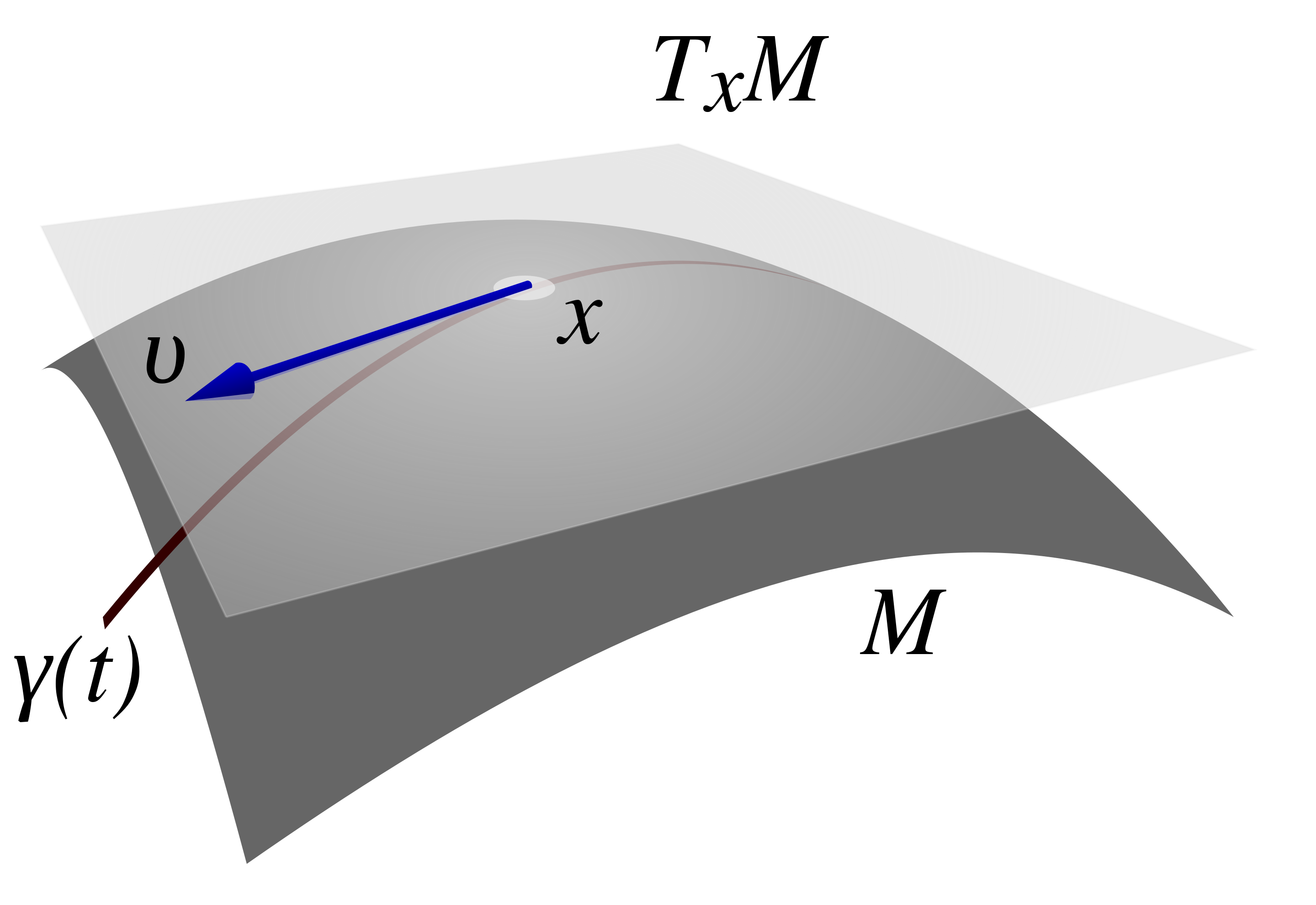
曲线的切矢量
设 $c : (-\epsilon,\epsilon) \rightarrow X$ 为流形 $X$ 上过 $p$ 点的一条曲线，其中 $c(0) = p$ 。则这条曲线给出一个映射：

$v_p:\mathscr{F}(X) \rightarrow \mathbb{R}$

定义为：

$v_p(f)=\frac{d(f\circ c(t))}{dt}|_ {t=0},\ \forall f\in \mathscr{F}(X)$

因为复合函数

$f\circ c:(-\epsilon,\epsilon) \rightarrow \mathbb{R}$

是在 $t=0$ 处的光滑函数，故求微商是有意义的。不难得到此处定义的 $v_p$ 满足前面切矢量的定义，因此它是流形 $X$ 上 $p$ 点的一个切矢量，称为曲线 $c(t)$ 在 $p$ 点的切矢量。

现在我们考虑选取一系列特殊的曲线。设 $p_0\in X$ 是流形上的任意一点， $(U,\varphi)$ 是包含 $p_0$ 的坐标卡，现在我们考虑过 $p_0$ 点的坐标曲线：

$c_j: (-\epsilon,\epsilon)\rightarrow X, j=1,\cdots,n$

定义为：

$x^i(c_j(t)) = x^i(p_0) + t\delta^i_j$

其中 $c(0)=p_0$ 。我们记曲线 $c_j(t)$ 在 $p_0$ 点的切矢量为 $e_j$ ，则按照曲线切矢量的定义，我们有：

$\begin{aligned} e_j(f) &= \frac{d(f\circ c_j(t))}{dt}|_{t=0}\\ &= \frac{d}{dt}(f\circ \varphi^{-1}\circ \varphi \circ c_j(t))|_{t=0}\\ &= \frac{d}{dt}(f\circ \varphi^{-1}(\varphi \circ c_j(t)))|_{t=0}\\ &= \frac{\partial(f\circ \varphi^{-1})}{\partial x^k}(\varphi\cdot c_j(t))\cdot \frac{dx^k(c_j(t))}{dt}|_{t=0}\\ &= \frac{\partial(f\circ \varphi^{-1})}{\partial x^k}|_{\varphi(p_0)}\delta^k_j\\ &= \frac{\partial(f\circ \varphi^{-1})}{\partial x^j}|_{\varphi(p_0)} \end{aligned}$

其中用到了：

$(\varphi\circ c_j(t))^k = x^k(c_j(t))$

以及复合函数求导的链式法则。

从而我们得到：

$e_j(f)=\frac{\partial (f\circ \varphi^{-1})}{\partial x^j}|_ {\varphi(p_0)}$

$e_i$ 在函数 $f$ 上的作用等价于其表示函数 $F = f\circ \varphi^{-1}$ 在 $\varphi(p_0 )$ 对 $x_i$ 的偏导数。

容易看出：若选取 $f$ 为某个坐标函数，如 $x^i$ ，则我们有：

$e_j (x^i) = \delta^i_{j}$

这样在 $p_0$ 点，我们得到了 $n$ 个切矢量，下面我们证明 $p_0$ 点的任意一个切矢量都可以表示成这 $n$ 个切矢量的线性组合。

有以下引理：
设 $x_0\in \mathbb{R}^n, F\in \mathscr{F}(\mathbb{R}^n)$ ，则 $F$ 可以表示为：

$F(x) = F(x_0) + (x^i-x_0^i)\frac{\partial F}{\partial x^i}|_{x_0}$

现假定 $f$ 是一个在点 $p_0\subset X$ 的某一邻域内的可微函数。在某一个相容的坐标卡 $(U,\varphi)$ 下，它可以表示为：

$F = f\circ \varphi^{-1}:\ V\rightarrow \mathbb{R}$

其中 $V \subset \mathbb{R}^n$ 包含 $p_0$ 点的像 $f(p_0) = F(\varphi(p_0))$ ，在 $f(p_0)$ 点我们可以对 $F$ 做展开：

$\begin{aligned} f(p) &= F(\varphi(p)) = F(\varphi(p_0)) + (x^i(p)-x^i(p_0))\frac{\partial F}{\partial x^i}|_{f(p_0)}\\ &= f(p_0) + (x^i(p)-x^i(p_0))\frac{\partial F}{\partial x^i}|_{f(p_0)}\\ \end{aligned}$

将 $v_{p_0}$ 作用到 $f$ 的这一表达式上得到：

$v_{p_0}(f) = v_{p_0}(x^i)\frac{\partial F}{\partial x^i}|_{\varphi(p_0)} = v_{p_0}(x^i)\frac{\partial (f\circ \varphi^{-1})}{\partial x^i}|_{\varphi(p_0)}$

结合切矢量 $e_i$ 在 $f$ 上的作用，我们得到：

$v_{p_0}(f) = v_{p_0}(x^i)e_i(f)$

因为 $f$ 是 $\mathscr{F}(x)$ 中的任意元素，从而我们得到：

$v_{p_0} = v_{p_0}(x^i)e_i = v_{p_0}^ie_i$

从而 $p_0$ 点的任意切矢量都可以用 $p_0$ 点的一组切矢量 $\{e_i,i=1,\cdots,n\}$ 线性组合给出。这个结论由于 $p$ 点选取的任意性推广到整个流形上。

容易证明 $\{e_i\}$ 是线性无关的。若假设 $a^ie_i = 0$ ，则我们得到：

$a^ie_i(x^j) = a^i\delta^{j}_{i} = a^j = 0$

所以 $\{e_i\}$ 是线性无关的，由此 $p$ 点所有的切矢量形成的线性空间 $T_pX$ 的维数为 $n$ 。而且在给定一个坐标卡之后，我们得到一组基底 $\{e_i\}$ ，通常我们将这个基称为 自然基 (natural basis)，并表示为：

$\{ e_i=\frac{\partial}{\partial x^i}|_ p,i = 1,\cdots ,n \}$

$v_p^i$ 是切矢量 $v_p$ 在这个自然基下的分量。

可以将切矢量用自然基展开为：

$v_p=\frac{dx^i(c(t))}{dt}| _ {t=0} \frac{\partial}{\partial x^i}|_ p$

设 $(\tilde{U},\tilde{\varphi})$ 是另外一个包含点 $p$ 的坐标卡，而相应的坐标函数为 $\tilde{x}^i$ ，因此 $p$ 点的任意一个切矢量 $v_p$ 可以展开为：

$v_p = v_p^ie_i = \tilde{v}_p^i\tilde{e}_i = \tilde{v}_p^i\frac{\partial}{\partial \tilde{x}^i}|_p$

现在将 $\tilde{e}_i$ 在 $\tilde{e}_i$ 下展开，即可得到切矢量分量的关系：

$\tilde{e}_i = \tilde{e}_i(x^j)e_j = \frac{\partial (x^j \circ \tilde{\varphi}^{-1})}{\partial\tilde{x}^i}|_{\tilde{\varphi}(p)}e_j$

从而，切矢量分量的关系为：

$v_p^j = A^j_{\ \ i}\tilde{v}^i_p$

这里：

$A^j_{\ \ i} = \frac{\partial (x^j \circ \tilde{\varphi}^{-1})}{\partial\tilde{x}^i}|_{\tilde{\varphi}(p)} = \frac{\partial (\varphi \circ \tilde{\varphi}^{-1})^j}{\partial\tilde{x}^i}|_{\tilde{\varphi}(p)}$

其中 $\varphi\circ \tilde\varphi^{-1}$ 正是两个坐标卡间的坐标变换。对于任意的 $p\in U\cap \tilde{U}$ ，我们有：

$\begin{aligned} x^j(p) &= (\varphi\circ \tilde{\varphi}^{-1})^j(\tilde{\varphi}(p))\\ &= (\varphi\circ \tilde{\varphi}^{-1})^j(\tilde x^1(p),\cdots,\tilde{x}^n(p))\\ \end{aligned}$

故 $x^j$ 是 $(\tilde{x}^1,\cdots,\tilde{x}^n)$ 的函数，我们可以将 $A^{j}_{\ \ i}$ 简记为：

$A^j_{\ \ i} = \frac{\partial x^j}{\partial \tilde{x}^i} = \frac{\partial x^j(\tilde{x}^1,\cdots,\tilde{x}^n)}{\partial \tilde{x}^i}$

即有：

$v_p^j = A^j_{\ \ i}\tilde{v}^i_p$

即：切矢量遵从逆变矢量分量的变换规律。

除了以上方式定义切空间外，还可以用其他方式定义切空间：

用等价关系定义切空间
两条过 $p$ 点的光滑曲线在 $p$ 点称为是相切的，如果它们在 $p$ 点具有相同的切矢量。据此人们可以得到切空间的另一种定义方式，即在所有过 $p$ 点的曲线形成的集合中建立一个等价关系:若 $c_1$ 和 $c_2$ 在 $p$ 点相切，则称 $c_1$ 和 $c_2$ 是等价的。这样我们便得到等价类的集合。可以证明这个等价类集合上具有自然的线性结构，形成 $n$ -维的线性空间。这便是 $p$ 点的切空间 $T_p M$ 。每个（过 $p$ 点）曲线的等价类对应于一个切矢量。