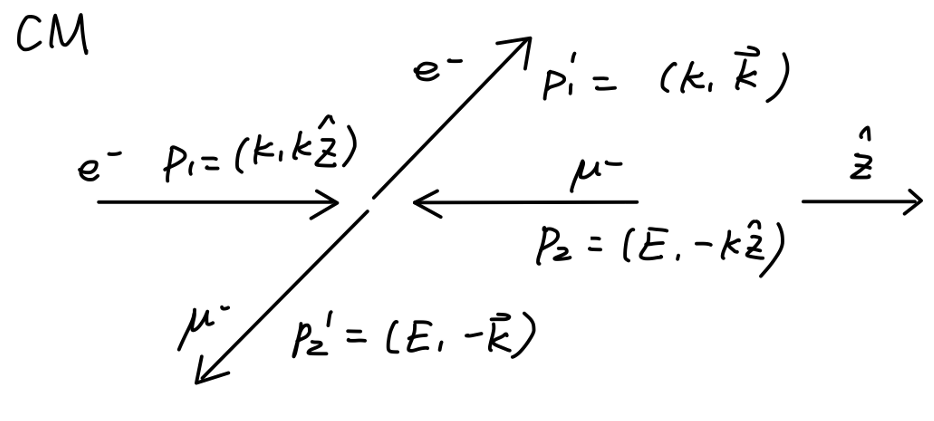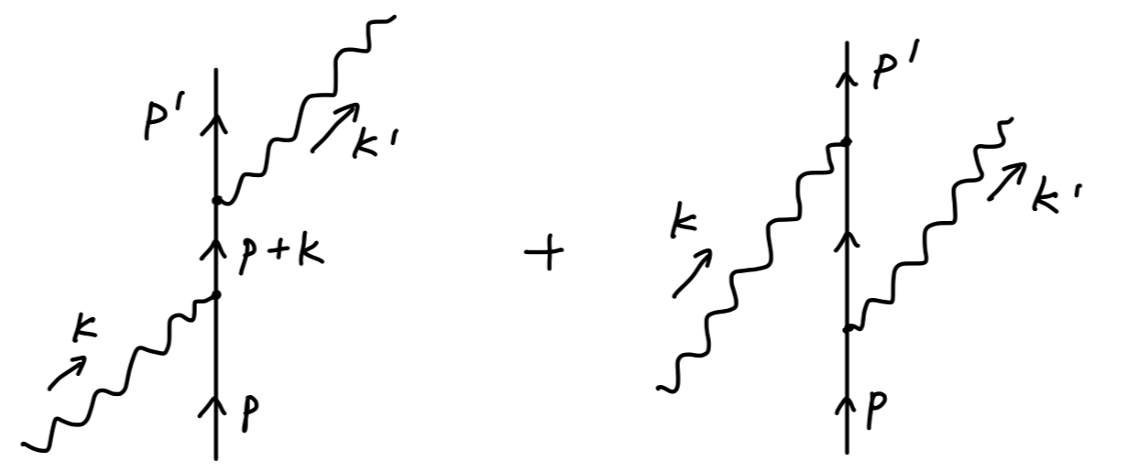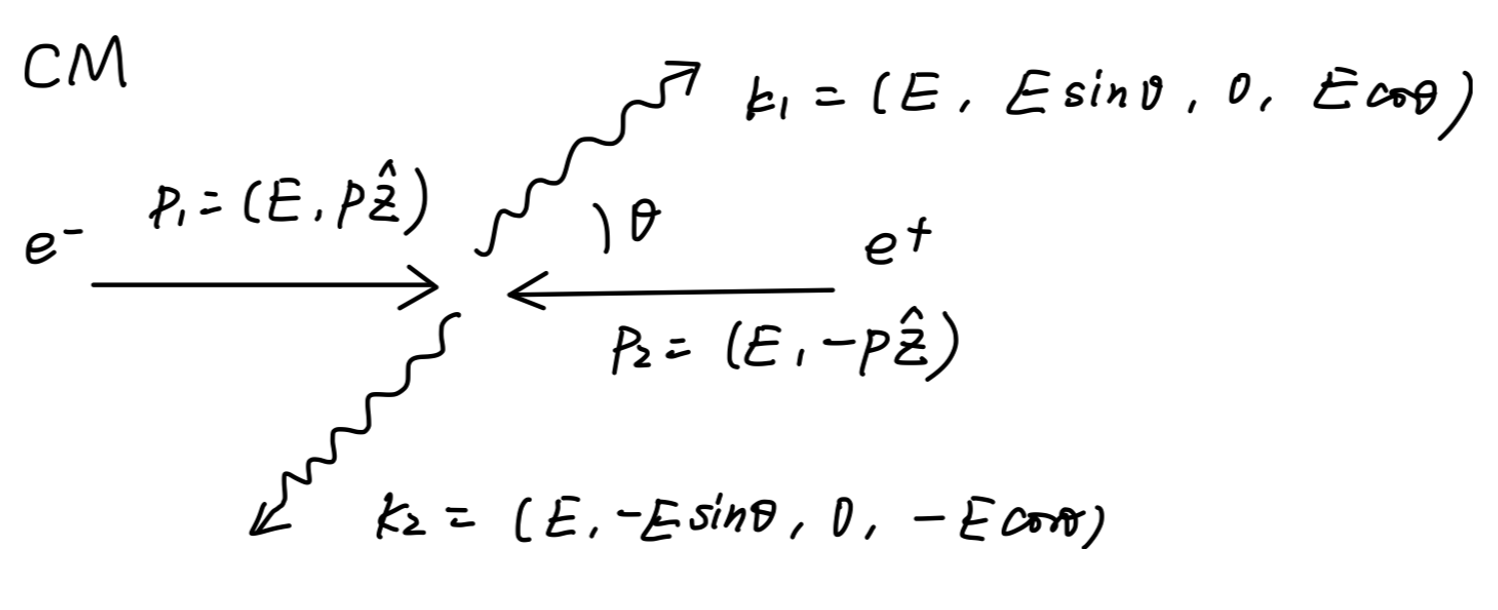ee-μ\mu 散射

现在我们考虑一个与 e−e+→μ−μ+e^{-}e^{+}\rightarrow \mu^{-}\mu^{+} 相类似的过程：ee-μ\mu 散射，即：e−μ−→e−μ−e^{-}\mu^{-}\rightarrow e^{-}\mu^{-}。其费曼图为：

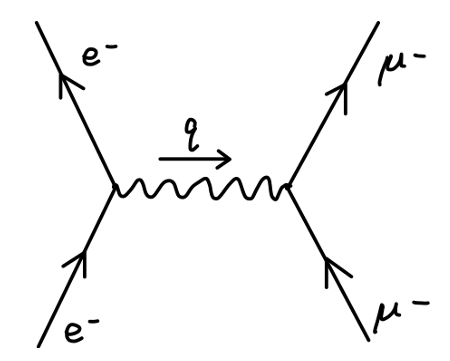
其跃迁矩阵元为：

iM=ie2q2uˉ(p1′)γμu(p1)uˉ(p2′)γμu(p2)(1)\begin{aligned} i\mathcal{M} &= \frac{ie^2}{q^2}\bar{u}(p_1')\gamma^{\mu}u(p_1)\bar{u}(p_2')\gamma_{\mu}u(p_2) \tag{1} \end{aligned}

对自旋求平均，由于 me≪mμm_e \ll m_{\mu}，可以令 me=0m_e=0：

14∑spins∣M∣2=e44q4tr[(p1+me)γμ(p1+me)γν]tr[(p2′+mμ)γμ(p2+mμ)γν]=8e4q4[(p1⋅p2′)(p1′⋅p2)+(p1⋅p2)(p1′⋅p2′)−mμ2(p1⋅p1′)](2)\begin{aligned} \frac{1}{4}\sum_{spins}|\mathcal{M}|^2 &= \frac{e^4}{4q^4}\mathrm{tr}[(\cancel p_1+m_e)\gamma^{\mu}(\cancel p_1 + m_e)\gamma^{\nu}]\mathrm{tr}[(\cancel p_2'+m_{\mu})\gamma_{\mu}(\cancel p_2 + m_{\mu})\gamma_{\nu}]\\ &= \frac{8e^4}{q^4}[(p_1\cdot p_2')(p'_1\cdot p_2) + (p_1\cdot p_2)(p'_1\cdot p_2') - m_{\mu}^2(p_1\cdot p_1')]\\ \end{aligned}\tag{2}

我们在质心系中写出各个粒子的四动量：

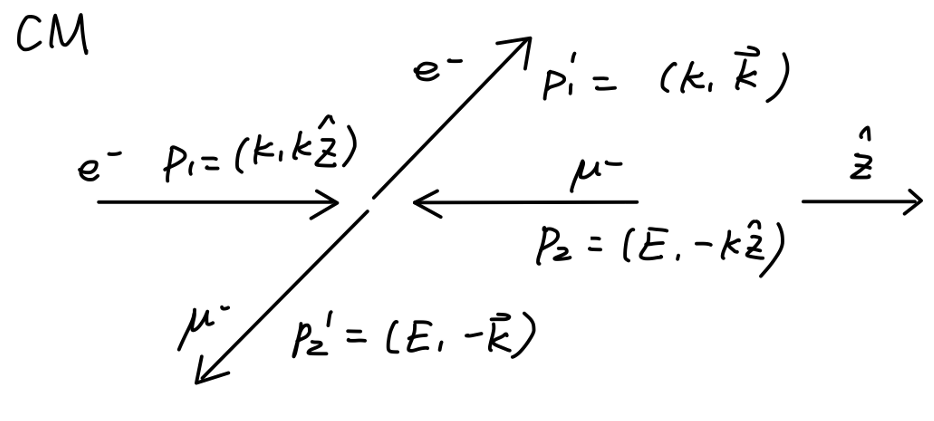
得到：

p1⋅p2=p1′⋅p2′=k(E+k)p1′⋅p2=p1⋅p2′=k(E+kcos⁡θ)p1⋅p1′=k2(1−cos⁡θ)q2=−2p1⋅p1′=−2k2(1−cos⁡θ)(3)\begin{aligned} &p_1\cdot p_2 = p_1'\cdot p_2' = k(E+k)\\ &p_1'\cdot p_2 = p_1 \cdot p_2' = k(E+k\cos\theta)\\ &p_1\cdot p_1' = k^2(1-\cos\theta)\\ &q^2 = -2p_1\cdot p_1'=-2k^2(1-\cos\theta)\\ \end{aligned}\tag{3}

代入 (4)(4) 得到：

14∑spins∣M∣2=8e44k4(1−cos⁡θ)2[k2(E+kcos⁡θ)2+k2(E+k)2−mμ2k2(1−cos⁡θ)]=2e4k2(1−cos⁡θ)2[(E+kcos⁡θ)2+(E+k)2−mμ2(1−cos⁡θ)](4)\begin{aligned} \frac{1}{4}\sum_{spins}|\mathcal{M}|^2 &= \frac{8e^4}{4k^4(1-\cos\theta)^2}[k^2(E+k\cos\theta)^2 + k^2(E+k)^2 - m_{\mu}^2k^2(1-\cos\theta)]\\ &= \frac{2e^4}{k^2(1-\cos\theta)^2}[(E+k\cos\theta)^2 + (E+k)^2 - m_{\mu}^2(1-\cos\theta)] \end{aligned}\tag{4}

得到微分散射截面为：

dσdΩ=∣M∣264π2(E+k)2=α22k2(E+k)2(1−cos⁡θ)2((E+k)2+(E+kcos⁡θ)2−mμ2(1−cos⁡θ))(5)\begin{aligned} \frac{d\sigma}{d\Omega} &= \frac{|\mathcal{M}|^2}{64\pi^2(E+k)^2}\\ &=\frac{\alpha^2}{2k^2(E+k)^2(1-\cos\theta)^2}((E+k)^2 + (E+k\cos\theta)^2 - m_{\mu}^2(1-\cos\theta))\\ \end{aligned}\tag{5}

在高能极限下，令 mμ→0,E→km_{\mu} \rightarrow 0 ,E \rightarrow k，有：

dσdΩ=α22Ecm2(1−cos⁡θ)2(4+(1+cos⁡θ)2)\begin{aligned} \frac{d\sigma}{d\Omega} &= \frac{\alpha^2}{2E_{cm}^2(1-\cos\theta)^2}(4+(1+\cos\theta)^2)\\ \end{aligned}

注意当 θ→0\theta\rightarrow 0 时，有：

dσdΩ∝1θ4(6)\frac{d\sigma}{d\Omega} \propto \frac{1}{\theta^4} \tag{6}

表明此时的微分散射截面存在奇异性。

交叉对称性

我们注意到过程 e+e−→μ+μ−e^{+}e^{-}\rightarrow \mu^+\mu^- 与 e−μ−→e−μ−e^{-}\mu^{-}\rightarrow e^{-}\mu^- 是相当类似的，从费曼图上来看：

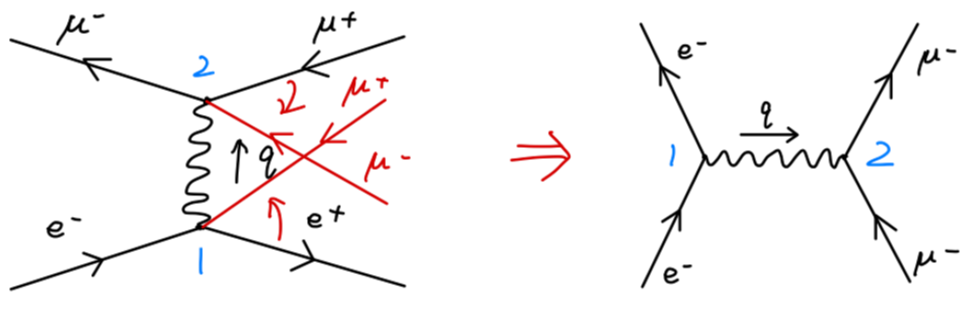
过程 e+e−→μ+μ−e^{+}e^{-}\rightarrow \mu^+\mu^- 与 e−μ−→e−μ−e^{-}\mu^{-}\rightarrow e^{-}\mu^- 之间的对称性称为 交叉对称性 crossing symmetry：对于一个包含动量为 pp 的初态正粒子的过程，和一个动量为 k=−pk = -p 的末态反粒子的过程是等价的，即：

M(ϕ(p)+⋯→⋯ )=M(⋯→⋯+ϕˉ(k))(7)\mathcal{M}(\phi(p)+\cdots\rightarrow \cdots) = \mathcal{M}(\cdots \rightarrow \cdots + \bar{\phi}(k)) \tag{7}

注意，ϕˉ\bar{\phi} 是 ϕ\phi 的反粒子，且 k=−pk = -p。因为正粒子与反粒子均要求：p0,k0>0p^0,k^0>0，所以并不存在一个值 pp，使得 ϕ(p)\phi(p) 与 ϕˉ(k)\bar{\phi}(k) 都是物理的。

这个关系用费曼图可以表示为：

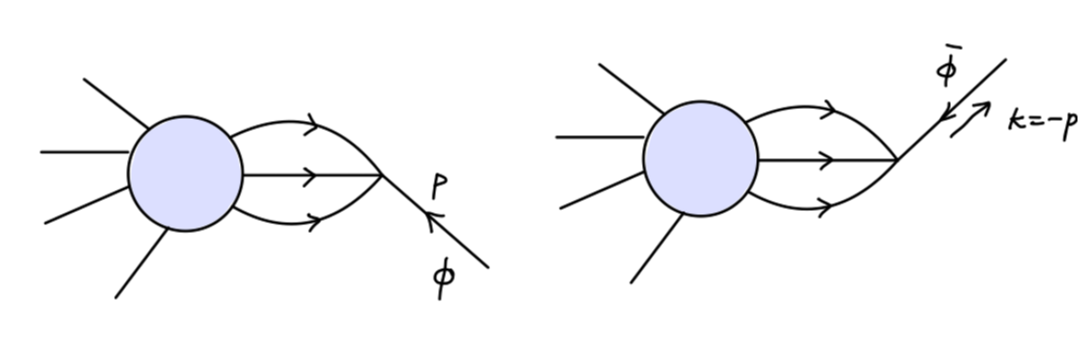
我们现在来举例说明这个关系的正确性：根据费曼规则：对于 ϕ\phi 是 Klein-Gordon 玻色子的情况是容易得到的；ϕ\phi 是 Dirac 费米子时，跃迁矩阵元 ∣M∣2|\mathcal{M}|^2 中出现：

∑sus(p)uˉs(p)=p+m=−(k−m)=−∑svs(p)vˉs(p)(8)\begin{aligned} \sum_{s} u^s(p)\bar{u}^s(p) = \cancel{p} + m = -(\cancel{k} - m) = - \sum_{s} v^s(p)\bar{v}^s(p) \tag{8} \end{aligned}

因此，我们只需要规定：在变换一个费米子时需要额外加上负号。那么就消去 (8)(8) 式子中的负号。

Mandelstam 变量

对于一个 a+b→c+da+b\rightarrow c+d 的过程，我们可以通过定义 Mandelstam 变量 Mandelstam variables 来简化计算：

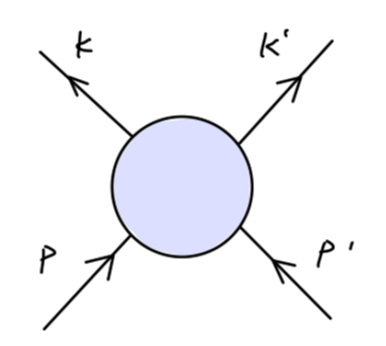
s=(p+p′)2=(k+k′)2t=(k−p)2=(k′−p′)2u=(k′−p)2=(k−p′)2(9)\begin{aligned} s = (p+p')^2 = (k+k')^2\\ t = (k-p)^2 = (k'-p')^2\\ u = (k'-p)^2 = (k-p')^2\\ \end{aligned}\tag{9}

如此，对于 e+e−→μ+μ−e^{+}e^{-}\rightarrow \mu^{+}\mu^{-} 过程

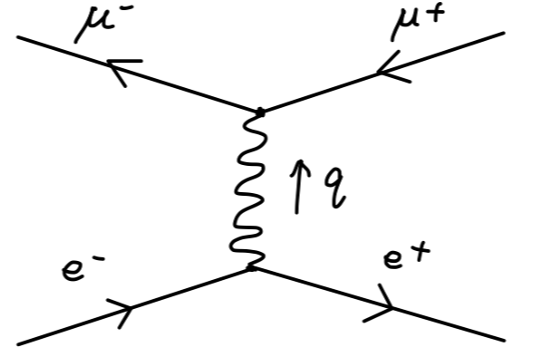
为了简化计算，我们在 me,mμ→0m_{e},m_{\mu}\rightarrow 0 下讨论问题，此时：

s=2p⋅p′=2k⋅k′t=−2k⋅p=−2k′⋅p′u=−2k′⋅p=−2k⋅p′(10)\begin{aligned} &s = 2p\cdot p' = 2k\cdot k'\\ &t = -2k\cdot p = -2k'\cdot p'\\ &u = -2k'\cdot p = -2k\cdot p'\\ \end{aligned}\tag{10}

可得

14∑spins∣M∣2=8e4q4[(p′⋅k)(p⋅k′)+(p⋅k)(p′⋅k′)]=8e4s2[(t2)2+(u2)2](11)\begin{aligned} \frac{1}{4}\sum_{spins}|\mathcal{M}|^2 &= \frac{8e^4}{q^4}[(p'\cdot k)(p\cdot k') + (p\cdot k)(p'\cdot k')]\\ & = \frac{8e^4}{s^2}[(\frac{t}{2})^2 + (\frac{u}{2})^2] \end{aligned}\tag{11}

对于 e−μ−→e−μ−e^{-}\mu^{-}\rightarrow e^{-}\mu^{-} 过程

s=2p1⋅p2=2p1′⋅p2′t=−2p1⋅p1′=−2p2⋅p2′u=−2p1′⋅p2=−2p1⋅p2′(12)\begin{aligned} &s = 2p_1\cdot p_2 = 2p_1'\cdot p_2'\\ &t = -2p_1\cdot p_1' = -2p_2\cdot p_2'\\ &u = -2p_1'\cdot p_2 = -2p_1\cdot p_2'\\ \end{aligned}\tag{12}

可得

14∑spins∣M∣2=8e4q4[(p1⋅p2′)(p1′⋅p2)+(p1⋅p2)(p1′⋅p2′)]=8e4t2[(u2)2+(s2)2](13)\begin{aligned} \frac{1}{4}\sum_{spins}|\mathcal{M}|^2 &= \frac{8e^4}{q^4}[(p_1\cdot p_2')(p'_1\cdot p_2) + (p_1\cdot p_2)(p'_1\cdot p_2')]\\ & = \frac{8e^4}{t^2}[(\frac{u}{2})^2 + (\frac{s}{2})^2] \end{aligned}\tag{13}

利用交叉对称性我们也能从对 e+e−→μ+μ−e^{+}e^{-}\rightarrow \mu^{+}\mu^{-} 过程的研究得到 e−μ−→e−μ−e^{-}\mu^{-}\rightarrow e^{-}\mu^{-} 过程的信息。我们只需要将 e+e^{+} 与 μ+\mu^{+} 改为对应的反粒子，并赋予一个相反的四动量，用费曼图表示为：

令

p′→−p′,k′→−k′p' \rightarrow -p', k' \rightarrow -k'

我们发现 (10)(10) 中的 Mandelstam variables 发生如下变化：

s→−2p⋅p′=−2k⋅k′t→−2k⋅p=−2k′⋅p′u→2k′⋅p=2k⋅p′(14)\begin{aligned} &s \rightarrow -2p\cdot p' = -2k\cdot k'\\ &t \rightarrow -2k\cdot p = -2k'\cdot p'\\ &u \rightarrow 2k'\cdot p = 2k\cdot p'\\ \end{aligned}\tag{14}

这正对应 e−μ−→e−μ−e^{-}\mu^{-}\rightarrow e^{-}\mu^{-} 的 Mandelstam variables 发生如下变化：

s→tt→uu→s(15)\begin{aligned} &s \rightarrow t\\ &t \rightarrow u\\ &u \rightarrow s\\ \end{aligned}\tag{15}

对应我们只需要将 (11)(11) 式的结果作 (15)(15) 式的代换就能得到 (13)(13)：

14∑spins∣M∣2=8e4t2[(s2)2+(u2)2]\frac{1}{4}\sum_{spins}|\mathcal{M}|^2 = \frac{8e^4}{t^2}[(\frac{s}{2})^2 + (\frac{u}{2})^2]

当 2→22\rightarrow 2 过程只含有一个虚粒子时，我们总可以用 s,u,ts,u,t 之一表示这个虚粒子的动量平方，这正好对应如下三种 channel：

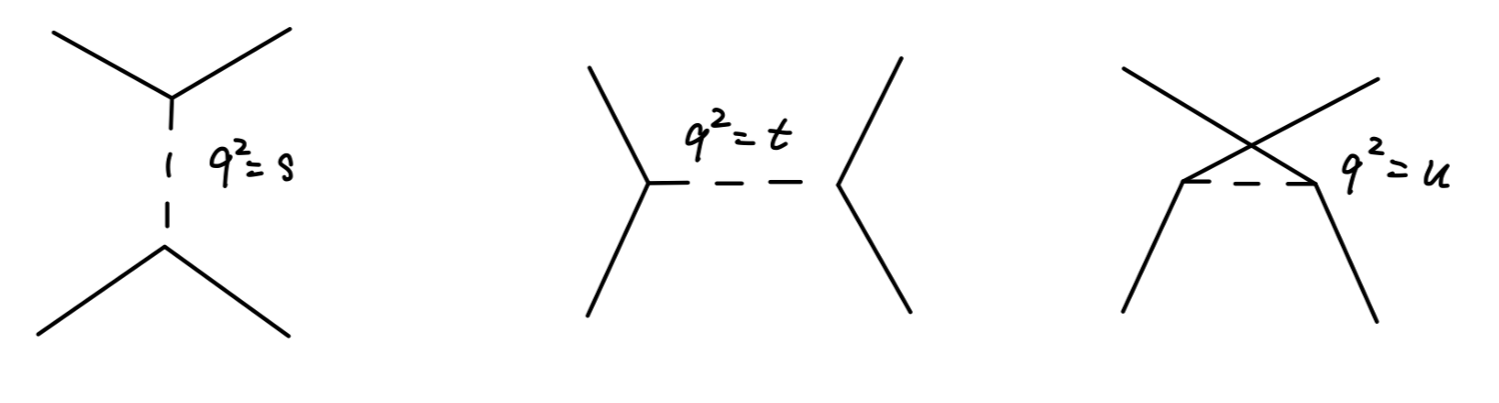
分别对应 s-channel,t-channel,u-channel 这正是 2→22\rightarrow 2 过程最低阶（tree-level）的三个费曼图。

s,t,us,t,u 具有以下一般性质：

s+t+u=(p+p′)2+(p−k)2+(p−k′)2=3p2+p′2+k2+k′2+2p⋅(p′−k−k′)=3p2+p′2+k2+k′2−2p2=∑i=14mi2(16)\begin{aligned} s + t + u &= (p+p')^2 + (p-k)^2 + (p-k')^2\\ &= 3p^2 +p'^2 + k^2 + k'^2 + 2p\cdot(p'-k-k')\\ &= 3p^2 +p'^2 + k^2 + k'^2 - 2p^2\\ &= \sum_{i=1}^{4}m_i^2\\ \end{aligned}\tag{16}

康普顿散射

接下来我们考虑 康普顿散射 compton scattering：e−γ→e−γe^{-}\gamma\rightarrow e^{-}\gamma。

其包括如下两个费曼图：

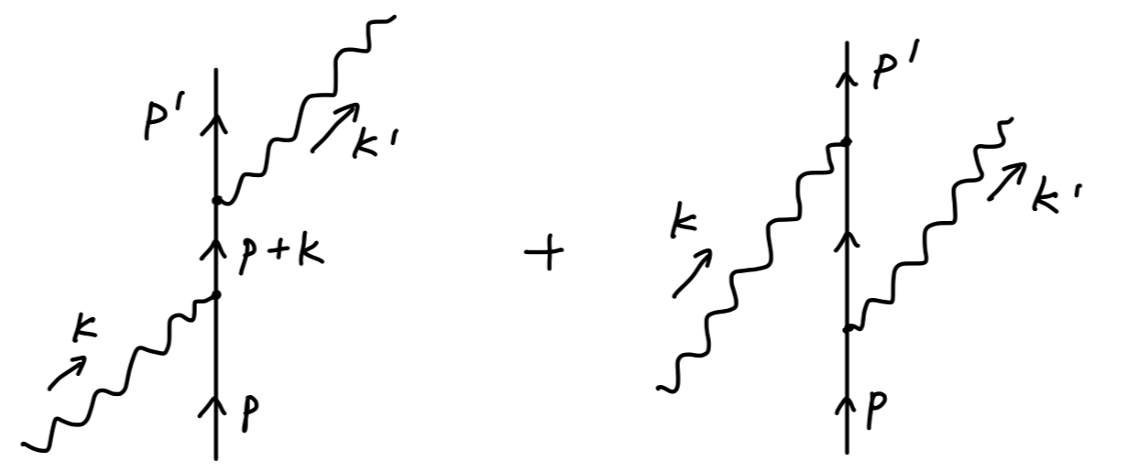
得到跃迁矩阵元为：

iM=uˉ(p′)(−ieγμ)ϵμ∗(k′)i(p+k+m)(p+k)2−m2(−ieγν)ϵν(k)u(p)+uˉ(p′)(−ieγν)ϵν(k)i(p−k′+m)(p−k′)2−m2(−ieγμ)ϵμ∗(k′)u(p)=−ie2ϵμ∗(k′)ϵν(k)uˉ(p′)(γμ(p+k+m)γν(p+k)2−m2+γν(p−k′+m)γμ(p−k′)2−m2)u(p)(17)\begin{aligned} \mathcal{i\mathcal{M}} =& \bar{u}(p')(-ie\gamma^{\mu})\epsilon^*_{\mu}(k')\frac{i(\cancel p+\cancel k+m)}{(p+k)^2-m^2}(-ie\gamma^{\nu})\epsilon_{\nu}(k)u(p)\\ &+ \bar{u}(p')(-ie\gamma^{\nu})\epsilon_{\nu}(k)\frac{i(\cancel p- \cancel k'+m)}{(p-k')^2-m^2}(-ie\gamma^{\mu})\epsilon^*_{\mu}(k')u(p)\\ =& -ie^2\epsilon_{\mu}^*(k')\epsilon_\nu(k)\bar{u}(p')(\frac{\gamma^{\mu}(\cancel p+\cancel k+m)\gamma^{\nu}}{(p+k)^2-m^2} + \frac{\gamma^{\nu}(\cancel p- \cancel k'+m)\gamma^{\mu}}{(p-k')^2-m^2})u(p) \end{aligned}\tag{17}

我们可以做一些化简：

(p+k)2−m2=2p⋅k(p−k′)2−m2=−2p⋅k′(18)\begin{aligned} &(p+k)^2 - m^2 = 2p\cdot k\\ &(p-k')^2 - m^2 = -2p\cdot k'\\ \end{aligned}\tag{18}

另外，有：

(p+m)γνu(p)=(2pν−γν(p−m))u(p)=2pνu(p)(19)\begin{aligned} (\cancel{p} + m)\gamma^{\nu}u(p) &= (2p^{\nu} - \gamma^{\nu}(\cancel{p}-m))u(p)\\ &= 2p^{\nu}u(p)\\ \end{aligned}\tag{19}

那么可以将跃迁矩阵元写为：

iM=−ie2ϵμ∗(k′)ϵν(k)uˉ(p′)(γμkγν+2γμpν2p⋅k+−γνk′γμ+2γνpμ−2p⋅k′)u(p)(20)i\mathcal{M} = -ie^2\epsilon_{\mu}^*(k')\epsilon_\nu(k)\bar{u}(p')(\frac{\gamma^{\mu}\cancel{k}\gamma^{\nu} + 2\gamma^{\mu}p^{\nu}}{2p\cdot k}+\frac{-\gamma^{\nu}\cancel{k}'\gamma^{\mu} + 2\gamma^{\nu}p^{\mu}}{-2p\cdot k'})u(p)\tag{20}

接下来，我们要将上式平方，并对所有可能的电子自旋与光子极化态求平均。类似电子旋量有关系：

∑uˉ(p)u(p)=p+m\sum \bar{u}(p)u(p) = \cancel{p} + m

极化矢量存在关系：

∑polarizationsϵμ∗ϵν→−gμν(21)\sum_{polarizations} \epsilon^*_{\mu}\epsilon_{\nu} \rightarrow -g_{\mu\nu} \tag{21}

不过 (21)(21) 式只有与跃迁矩阵元 Mμ\mathcal{M}^{\mu} 点积在一起时才有意义，即下式是严格成立的：

∑polarizationsϵμ∗ϵνMμMν∗→−gμνMμMν∗\sum_{polarizations} \epsilon^*_{\mu}\epsilon_{\nu}\mathcal{M}^{\mu}\mathcal{M}^{\nu*}\rightarrow -g_{\mu\nu}\mathcal{M}^{\mu}\mathcal{M}^{\nu*}

利用 (20)(21)(20)(21) 式得到：

14∑∣M∣2=e44gμρgνσtr((p′+m)(γμkγν+2γμpν2p⋅k+−γνk′γμ+2γνpμ−2p⋅k′)   ⋅(p+m)(γσkγρ+2γρpσ2p⋅k+−γρk′γσ+2γσpρ−2p⋅k′)=e44(I(2p⋅k)2+II(2p⋅k)(2p⋅k′)+III(2p⋅k′)(2p⋅k)+IV(2p⋅k′)2)(22)\begin{aligned} \frac{1}{4}\sum|\mathcal{M}|^2 &= \frac{e^4}{4}g_{\mu\rho}g_{\nu\sigma}\mathrm{tr}((\cancel{p}' +m)(\frac{\gamma^{\mu}\cancel{k}\gamma^{\nu} + 2\gamma^{\mu}p^{\nu}}{2p\cdot k}+\frac{-\gamma^{\nu}\cancel{k}'\gamma^{\mu} + 2\gamma^{\nu}p^{\mu}}{-2p\cdot k'})\\ &\qquad\qquad\quad\ \ \ \cdot (\cancel{p} +m)(\frac{\gamma^{\sigma}\cancel{k}\gamma^{\rho} + 2\gamma^{\rho}p^{\sigma}}{2p\cdot k}+\frac{-\gamma^{\rho}\cancel{k}'\gamma^{\sigma} + 2\gamma^{\sigma}p^{\rho}}{-2p\cdot k'})\\ &=\frac{e^4}{4}(\frac{\mathrm{I}}{(2p\cdot k)^2} + \frac{\mathrm{II}}{(2p\cdot k)(2p \cdot k')} + \frac{\mathrm{III}}{(2p\cdot k')(2p \cdot k)} + \frac{\mathrm{IV}}{(2p \cdot k')^2}) \end{aligned}\tag{22}

其中 I,II,III,IV\mathrm{I,II,III,IV} 都是一些矩阵的迹：

I=tr[(p′+m)(γμkγν+2γμpν)(p+m)(γνkγμ+2γμpν)]II=tr[(p′+m)(γμkγν+2γμpν)(p+m)(γμk′γν−2γνpμ)]III=tr[(p′+m)(γνk′γμ−2γνpμ)(p+m)(γνkγμ+2γμpν)]IV=tr[(p′+m)(γνk′γμ−2γνpμ)(p+m)(γμk′γν−2γνpμ)](23)\begin{aligned} \mathrm{I} &= \mathrm{tr}[(\cancel{p}' + m)(\gamma^{\mu}\cancel{k} \gamma^{\nu} + 2\gamma^{\mu}p^{\nu})(\cancel{p} + m)(\gamma_{\nu}\cancel{k} \gamma_{\mu} + 2\gamma_{\mu}p_{\nu})]\\ \mathrm{II} &= \mathrm{tr}[(\cancel{p}' + m)(\gamma^{\mu}\cancel{k} \gamma^{\nu} + 2\gamma^{\mu}p^{\nu})(\cancel{p} + m)(\gamma_{\mu}\cancel{k}' \gamma_{\nu} - 2\gamma_{\nu}p_{\mu})]\\ \mathrm{III} &= \mathrm{tr}[(\cancel{p}' + m)(\gamma^{\nu}\cancel{k}' \gamma^{\mu} - 2\gamma^{\nu}p^{\mu})(\cancel{p} + m)(\gamma_{\nu}\cancel{k} \gamma_{\mu} + 2\gamma_{\mu}p_{\nu})]\\ \mathrm{IV} &= \mathrm{tr}[(\cancel{p}' + m)(\gamma^{\nu}\cancel{k}' \gamma^{\mu} - 2\gamma^{\nu}p^{\mu})(\cancel{p} + m)(\gamma_{\mu}\cancel{k}' \gamma_{\nu} - 2\gamma_{\nu}p_{\mu})]\\ \end{aligned}\tag{23}

通过作交换 k,−k′k,-k'，I,IV\mathrm{I},\mathrm{IV} 的值交换；而 II,III\mathrm{II},\mathrm{III} 的值容易看出是相同的，因此我们只需要去计算 I\mathrm{I}。

我们首先考虑 I\mathrm{I}：

I=tr[(p′+m)(γμkγν+2γμpν)(p+m)(γνkγμ+2γμpν)](24)\begin{aligned} \mathrm{I} &= \mathrm{tr}[(\cancel{p}' + m)(\gamma^{\mu}\cancel{k} \gamma^{\nu} + 2\gamma^{\mu}p^{\nu})(\cancel{p} + m)(\gamma_{\nu}\cancel{k} \gamma_{\mu} + 2\gamma_{\mu}p_{\nu})]\\ \end{aligned}\tag{24}

其可以展开为 1616 项，但考虑含有奇数次 γ\gamma 矩阵的项的迹为零（一共 88 项），如此。另外 88 项需要进行计算，例如：

tr(p′γμkγνpγνkγμ)=tr(γμp′γμkγνpγνk)=tr((−2p′)k(−2p)k)=tr(4p′k(2p⋅k−kp))=8p⋅ktr(p′k)=32(p⋅k)(p⋅k′)\begin{aligned} &\mathrm{tr}(\cancel{p}' \gamma^{\mu}\cancel{k}\gamma^{\nu}\cancel{p} \gamma_{\nu}\cancel{k} \gamma_{\mu})\\ =&\mathrm{tr}(\gamma_{\mu}\cancel{p}' \gamma^{\mu}\cancel{k}\gamma^{\nu}\cancel{p} \gamma_{\nu}\cancel{k} )\\ =& \mathrm{tr}((-2\cancel{p}')\cancel{k}(-2\cancel{p})\cancel{k} )\\ =&\mathrm{tr}(4\cancel{p}'\cancel{k} (2p\cdot k - \cancel{k}\cancel{p}))\\ =&8 p\cdot k\mathrm{tr}(\cancel{p}'\cancel{k})\\ =&32(p\cdot k)(p\cdot k') \end{aligned}

上述推导中用到了 kk=k2=0\cancel{k}\cancel{k} = k^2 = 0

最终可得：

I=16(4m2−2m2p⋅p′+4m2p⋅k−2m2p′⋅k+2(p⋅k)(p′⋅k))(25)\mathrm{I} = 16(4m^2 - 2m^2p\cdot p' + 4m^2p\cdot k - 2m^2 p'\cdot k + 2(p\cdot k)(p'\cdot k)) \tag{25}

将 Mandelstam variables 代入得到：

s=(p+k)2=2p⋅k+m2=2p′⋅k′+m2t=(p′−p)2=−2p⋅p′+2m2=−2k⋅k′u=(k′−p)2=−2k′⋅p+m2=−2k⋅p′+m2\begin{aligned} & s = (p+k)^2 = 2p\cdot k +m^2 = 2p'\cdot k' +m^2\\ & t = (p'-p)^2 = -2p\cdot p' +2m^2 = -2k\cdot k'\\ & u = (k'-p)^2 = -2k'\cdot p + m^2 = -2k\cdot p' + m^2\\ \end{aligned}

得到：

I=16(2m4+m2(s−m2)−12(s−m2)(u−m2))(26)\mathrm{I} = 16(2m^4 + m^2(s-m^2) - \frac{1}{2}(s-m^2)(u-m^2)) \tag{26}

通过代换 k′↔−kk'\leftrightarrow -k，即 s↔us \leftrightarrow u，得到：

IV=16(2m4+m2(u−m2)−12(s−m2)(u−m2))(27)\mathrm{IV} = 16(2m^4 + m^2(u-m^2) - \frac{1}{2}(s-m^2)(u-m^2)) \tag{27}

类似的，计算得到：

II=III=−8(4m2+m2(s−m2)+m2(u−m2))(28)\begin{aligned} &\mathrm{II} = \mathrm{III} =-8(4m^2 + m^2(s-m^2)+ m^2(u-m^2))\\ \end{aligned}\tag{28}

将计算出的 (26)(27)(28)(26)(27)(28) 代入 (22)(22)，最终得到：

14∑∣M∣2=2e4[p⋅k′p⋅k+p⋅kp⋅k′+2m2(1p⋅k−1p⋅k′)+m4(1p⋅k−1p⋅k′)2](29)\frac{1}{4}\sum |\mathcal{M}|^2 = 2e^4[\frac{p\cdot k'}{p\cdot k} + \frac{p\cdot k}{p\cdot k'} + 2m^2(\frac{1}{p\cdot k}-\frac{1}{p\cdot k'}) + m^4(\frac{1}{p\cdot k}-\frac{1}{p\cdot k'})^2]\tag{29}

我们现在在实验系中计算康普顿散射的截面。此时，电子是静止的，光子的频率为 ω\omega。

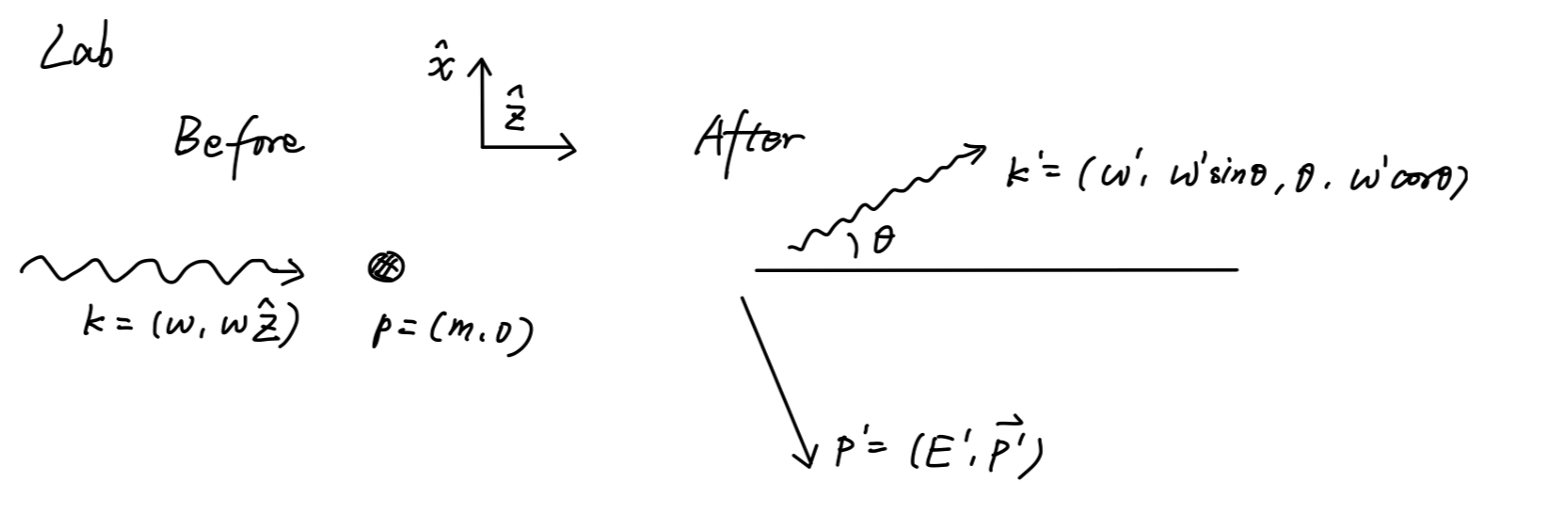
对于康普顿散射来说，根据四动量守恒，可以计算得到末态光子的频率：

1ω′−1ω=1m(1−cos⁡θ)(30)\frac{1}{\omega'}-\frac{1}{\omega} = \frac{1}{m}(1-\cos\theta) \tag{30}

得到：

p⋅k=mωp⋅k′=mω′(31)p\cdot k = m\omega \quad p\cdot k' = m\omega' \tag{31}

代入 (29)(29)，得到：

14∑∣M∣2=2e4(ω′ω+ωω′+2m(1ω−1ω′)+m2(1ω−1ω′)2)=2e4(ω′ω+ωω′+2(cos⁡θ−1)+(cos⁡θ−1)2)=2e4(ω′ω+ωω′−sin⁡2θ)(32)\begin{aligned} \frac{1}{4}\sum |\mathcal{M}|^2 &= 2e^4(\frac{\omega'}{\omega} + \frac{\omega}{\omega'} + 2m(\frac{1}{\omega}-\frac{1}{\omega'}) + m^2(\frac{1}{\omega}-\frac{1}{\omega'})^2)\\ &= 2e^4(\frac{\omega'}{\omega} + \frac{\omega}{\omega'} + 2(\cos\theta-1) + (\cos\theta-1)^2)\\ &= 2e^4(\frac{\omega'}{\omega} + \frac{\omega}{\omega'} - \sin^2\theta)\\ \end{aligned}\tag{32}

另外，(30)(30) 可以显式地写为：

ω′=ω1+ωm(1−cos⁡θ)(33)\omega' = \frac{\omega}{1 + \frac{\omega}{m}(1-\cos\theta)} \tag{33}

为了计算散射截面，我们要对相空间进行积分：

∫d3k′(2π)312ω′∫d3p(2π)312E′(2π)4δ(4)(p′+k′−p−k)=∫d3k′(2π)314ω′E′2πδ(E′+ω′−ω−m)=∫dΩω′2dω′(2π)314ω′E′2πδ(m2+p′2+ω′−ω−m)=∫dΩω′dω′(2π)314E′2πδ(ω′+m2+ω2+ω′2−2ωω′cos⁡θ−ω−m)=∫dΩ(2π)3ω′4E′2π1∣1+ω′−ωcos⁡θE′∣=∫dcos⁡θ2πω′4E′1∣1+ω′−ωcos⁡θE′∣=18π∫dcos⁡θω′m+ω(1−cos⁡θ)=18π∫dcos⁡θω′2mω\begin{aligned} &\int \frac{d^3k'}{(2\pi)^3} \frac{1}{2\omega'} \int \frac{d^3p}{(2\pi)^3} \frac{1}{2E'} (2\pi)^4 \delta^{(4)}(p'+k'-p-k)\\ =& \int \frac{d^3k'}{(2\pi)^3} \frac{1}{4\omega'E'} 2\pi \delta(E' + \omega' - \omega -m)\\ =& \int \frac{d\Omega \omega'^2d\omega'}{(2\pi)^3} \frac{1}{4\omega'E'} 2\pi \delta(\sqrt{m^2 + \bm{p}'^2} + \omega' - \omega -m)\\ =& \int \frac{d\Omega \omega'd\omega'}{(2\pi)^3} \frac{1}{4E'} 2\pi \delta(\omega' + \sqrt{m^2 + \omega^2 + \omega'^2 - 2\omega\omega'\cos\theta} - \omega -m)\\ =& \int \frac{d\Omega}{(2\pi)^3} \frac{\omega'}{4E'} 2\pi \frac{1}{|1 + \frac{\omega' - \omega \cos\theta}{E'}|}\\ =& \int \frac{d\cos\theta}{2\pi} \frac{\omega'}{4E'} \frac{1}{|1 + \frac{\omega' - \omega \cos\theta}{E'}|}\\ =& \frac{1}{8\pi} \int d\cos\theta \frac{\omega'}{m+\omega(1-\cos\theta)}\\ =& \frac{1}{8\pi}\int d\cos\theta \frac{\omega'^2}{m\omega} \end{aligned}

令两粒子的相对速度为 11，得到微分散射截面的表达式：

dσdcos⁡θ=18π12m12ωω′2mω2e4(ω′ω+ωω′−sin⁡2θ)=e4ω′216πm2ω2(ω′ω+ωω′−sin⁡2θ)\begin{aligned} \frac{d\sigma}{d\cos\theta} &= \frac{1}{8\pi} \frac{1}{2m}\frac{1}{2\omega} \frac{\omega'^2}{m\omega} 2e^4(\frac{\omega'}{\omega} + \frac{\omega}{\omega'} - \sin^2\theta)\\ &= \frac{e^4\omega'^2}{16\pi m^2\omega^2}(\frac{\omega'}{\omega} + \frac{\omega}{\omega'} - \sin^2\theta)\\ \end{aligned}

将精细结构常数 α=e2/4π\alpha = e^2/4\pi 作替换，得到：

dσdcos⁡θ=πα2m2(ω′ω)2(ω′ω+ωω′−sin⁡2θ)(34)\frac{d\sigma}{d\cos\theta} = \frac{\pi \alpha^2}{m^2}(\frac{\omega'}{\omega})^2(\frac{\omega'}{\omega} + \frac{\omega}{\omega'} - \sin^2\theta)\tag{34}

这称为 Klein-Nishina 公式 Klein-Nishina formula。

现在讨论康普顿散射在低能与高能下的行为。

首先，对于低能情况，取 ω→0\omega \rightarrow 0，有：ωω′→1\frac{\omega}{\omega'} \rightarrow 1。代入 (34)(34) 式，得到：

dσdcos⁡θ=πα2m2(1+cos⁡2θ)(35)\frac{d\sigma}{d\cos\theta} = \frac{\pi \alpha^2}{m^2}(1 + \cos^2\theta) \tag{35}

总截面为：

σtotal=8πα23m2(36)\sigma_{total} = \frac{8\pi \alpha^2}{3m^2} \tag{36}

对于高能情况，我们在质心系中讨论问题：

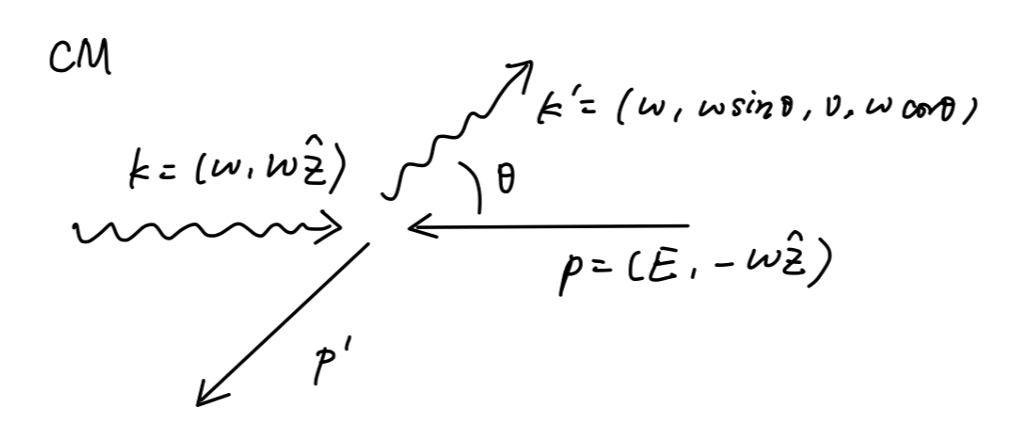
此时有：

p⋅k=ω(E+ω)p⋅k′=ω(E+ωcos⁡θ)E2=ω2+m2(37)p\cdot k = \omega(E+\omega)\quad p\cdot k' = \omega(E+\omega\cos\theta)\quad E^2 = \omega^2 + m^2 \tag{37}

以及：

ω,ω′≫m,θ≈π\omega,\omega' \gg m,\quad \theta \approx \pi

将 (37)(37) 代入 (29)(29) 得到：

14∑∣M∣2≈2e4p⋅kp⋅k′=2e4E+ωE+ωcos⁡θ\begin{aligned} \frac{1}{4}\sum |\mathcal{M}|^2 &\approx 2e^4\frac{p\cdot k}{p\cdot k'}\\ &= 2e^4 \frac{E+\omega}{E+\omega\cos\theta}\\ \end{aligned}

在质心系中的微分散射截面成为：

dσdcos⁡θ=18π12E12ωω2π⋅4(E+ω)2e4E+ωE+ωcos⁡θ≈2πα22m2+s(1+cos⁡θ)(38)\begin{aligned} \frac{d\sigma}{d\cos\theta} &= \frac{1}{8\pi} \frac{1}{2E}\frac{1}{2\omega} \frac{\omega}{2\pi\cdot 4(E+\omega)} 2e^4 \frac{E+\omega}{E+\omega\cos\theta}\\ &\approx \frac{2\pi\alpha^2}{2m^2+s(1+\cos\theta)}\\ \end{aligned}\tag{38}

我们可以作一些近似，由于 s≫m2s\gg m^2，得到：

dσdcos⁡θ≈2πα2s(1+cos⁡θ)(39)\frac{d\sigma}{d\cos\theta} \approx \frac{2\pi\alpha^2}{s(1+\cos\theta)}\tag{39}

但该式相比 (38)(38) 而言在 θ=π\theta = \pi 时具有奇异性，因此为了计算总散射截面，我们需要修改以下积分限。令：

s(1+cos⁡θ)=2m2→cos⁡θ=2m2s−1(40)s(1+\cos\theta) = 2m^2 \rightarrow \cos\theta = \frac{2m^2}{s} - 1 \tag{40}

因此，总散射截面成为：

σtotal=∫−1+2m2s1dcos⁡θdσdcos⁡θ=∫−1+2m2s1dcos⁡θ2πα2s(1+cos⁡θ)=2πα2s∫−1+2m2s1dcos⁡θ1+cos⁡θ=2πα2sln⁡(sm2)(41)\begin{aligned} \sigma_{total} &= \int_{-1+\frac{2m^2}{s}}^{1} d\cos\theta\frac{d\sigma}{d\cos\theta}\\ &= \int_{-1+\frac{2m^2}{s}}^{1} d\cos\theta \frac{2\pi\alpha^2}{s(1+\cos\theta)}\\ &= \frac{2\pi\alpha^2}{s} \int_{-1+\frac{2m^2}{s}}^{1} \frac{d\cos\theta}{1+\cos\theta}\\ &= \frac{2\pi\alpha^2}{s} \ln (\frac{s}{m^2}) \end{aligned} \tag{41}

正负电子对湮灭

利用交叉对称性，可以将康普顿散射与正负电子对湮灭关联起来：

e+e−→2γe^{+}e^{-} \rightarrow 2\gamma

用费曼图表示为：

在康普顿散射中，我们只需要做以下代换：

p→p1p′→−p2k→−k1k′→k2(42)p \rightarrow p_1\quad p' \rightarrow -p_2\quad k\rightarrow -k_1 \quad k'\rightarrow k_2 \tag{42}

代入 (29)(29) 得到跃迁矩阵元为：

14∑∣M∣2=−2e4[p1⋅k2p1⋅k1+p1⋅k1p1⋅k2+2m2(1p1⋅k1+1p1⋅k2)−m4(1p1⋅k1+1p1⋅k2)2](43)\frac{1}{4}\sum |\mathcal{M}|^2 = -2e^4[\frac{p_1\cdot k_2}{p_1\cdot k_1} + \frac{p_1\cdot k_1}{p_1\cdot k_2} + 2m^2(\frac{1}{p_1\cdot k_1}+\frac{1}{p_1\cdot k_2}) - m^4(\frac{1}{p_1\cdot k_1}+\frac{1}{p_1\cdot k_2})^2]\tag{43}

在质心系中进行计算：

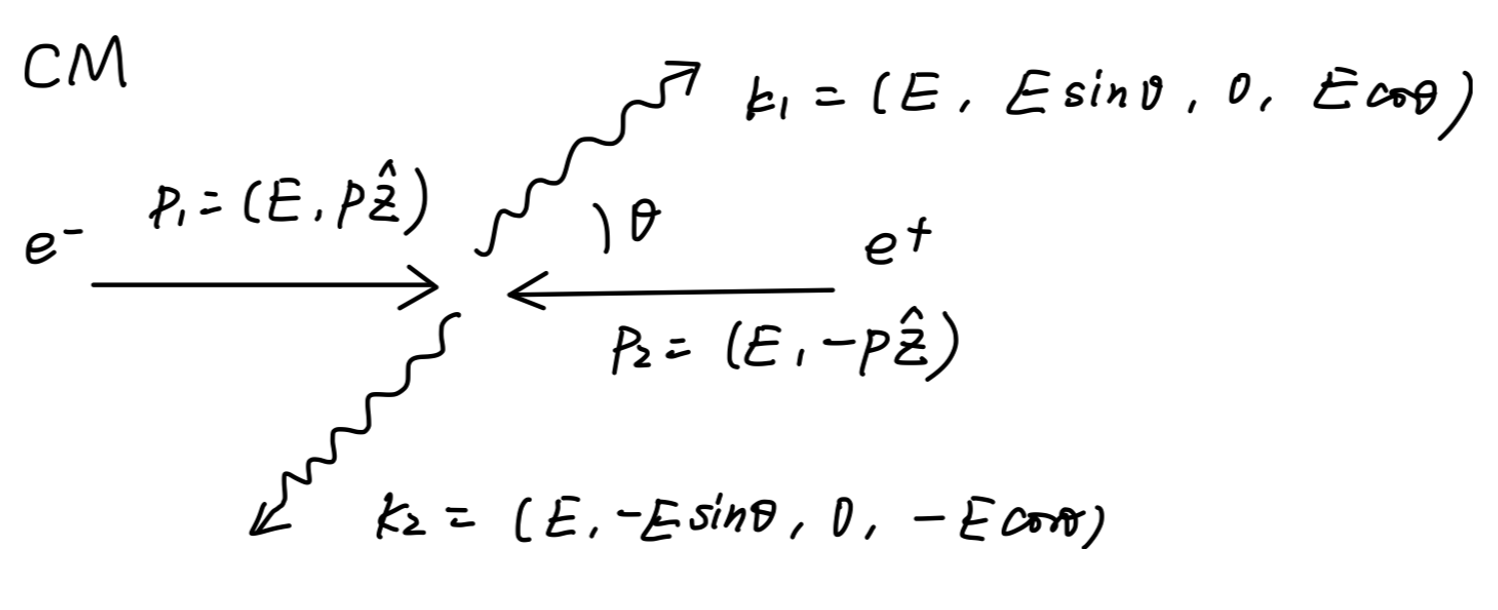
p1⋅k1=E(E−pcos⁡θ)p1⋅k2=E(E+pcos⁡θ)(44)p_1\cdot k_1 = E(E-p\cos\theta)\quad p_1\cdot k_2 = E(E+p\cos\theta) \tag{44}

代入 (43)(43) 式，得到：

14∑∣M∣2=−2e4[E+pcos⁡θE−pcos⁡θ+E−pcos⁡θE+pcos⁡θ+2m2(1E(E−pcos⁡θ)+1E(E+pcos⁡θ))−m4(1E(E−pcos⁡θ)+1E(E+pcos⁡θ))2]=−4e4[E2+p2cos⁡2θm2+p2sin⁡2θ+2m2m2+p2sin⁡2θ−2m4(m2+p2sin⁡2θ)2]\begin{aligned} \frac{1}{4}\sum |\mathcal{M}|^2 &= -2e^4[\frac{E+p\cos\theta}{E-p\cos\theta} + \frac{E-p\cos\theta}{E+p\cos\theta} + 2m^2(\frac{1}{E(E-p\cos\theta)}+ \frac{1}{E(E+p\cos\theta)})\\ &\quad -m^4(\frac{1}{E(E-p\cos\theta)} + \frac{1}{E(E+p\cos\theta)})^2]\\ &= -4e^4 [\frac{E^2+p^2\cos^2\theta}{m^2+p^2\sin^2\theta} + \frac{2m^2}{m^2+p^2\sin^2\theta} - \frac{2m^4}{(m^2+p^2\sin^2\theta)^2}] \end{aligned}

对应的微分散射截面为：

dσdcos⁡θ=2πα2s(Ep)[E2+p2cos⁡2θm2+p2sin⁡2θ+2m2m2+p2sin⁡2θ−2m4(m2+p2sin⁡2θ)2]\frac{d\sigma}{d\cos\theta} = \frac{2\pi\alpha^2}{s}(\frac{E}{p}) [\frac{E^2+p^2\cos^2\theta}{m^2+p^2\sin^2\theta} + \frac{2m^2}{m^2+p^2\sin^2\theta} - \frac{2m^4}{(m^2+p^2\sin^2\theta)^2}]

在高能极限下，有 E≈p≫mE \approx p \gg m，因此上式成为：

dσdcos⁡θ→2πα2s1+cos⁡2θsin⁡2θ\frac{d\sigma}{d\cos\theta} \rightarrow \frac{2\pi\alpha^2}{s}\frac{1+\cos^2\theta}{\sin^2\theta}