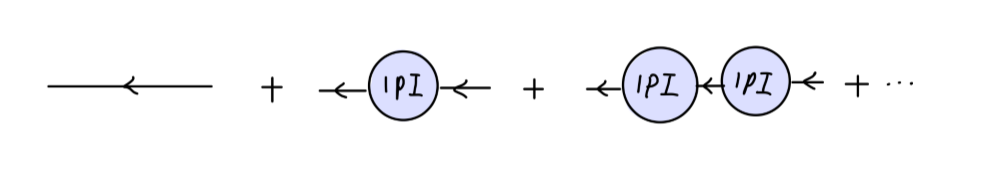场强重整化

两点关联函数的结构

我们现在来研究如下两点关联函数的解析性质。

⟨Ω∣Tϕ(x)ϕ(y)∣Ω⟩\langle \Omega|T\phi(x)\phi(y)|\Omega\rangle

对于自由场的两点关联函数来说，有：

⟨0∣Tϕ(x)ϕ(y)∣0⟩=DF(x−y)=∫d4p(2π)4ip2−m2+iϵe−ip(x−y)\langle 0|T\phi(x)\phi(y)|0\rangle = D_F(x-y) = \int \frac{d^4p}{(2\pi)^4}\frac{i}{p^2-m^2+i\epsilon}e^{-ip(x-y)}

p2=m2p^2 = m^2 为该传播子的极点，对应一个质量为 mm 的自由粒子态。

为了观察一般的两点关联函数，我们首先在两个场量间插入一个恒等算子。常用的技巧，我们利用完备性写出恒等算子。

对于单粒子态来说，有：

(1)1−particle=∫d3p(2π)312Ep∣p⟩⟨p∣(1)_{1-particle} = \int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}|\bm{p}\rangle\langle \bm{p}|

现在我们做一些推广。对于一个哈密顿量 HH 的零动量本征态 ∣λ0⟩|\lambda_0\rangle 有 P^∣λ0⟩=0\hat{\bm{P}}|\lambda_0\rangle = 0。那么对 ∣λ0⟩|\lambda_0\rangle 态的所有 boost 实际上也是哈密顿量的本征态。我们定义 ∣λp⟩|\lambda_{\bm{p}}\rangle 为 ∣λ0⟩|\lambda_0\rangle 经过 boost 后得到的动量为 p\bm{p} 的态。其能量为：Ep≡∣p∣2+mλ2E_{\bm{p}} \equiv \sqrt{|\bm{p}|^2 + m^2_{\lambda}}。那么，我们所期望的完备性关系为：

1=∣Ω⟩⟨Ω∣+∑λ∫d3p(2π)312Ep(λ)∣λp⟩⟨λp∣1 = |\Omega\rangle\langle\Omega| + \sum_{\lambda}\int \frac{d^3p}{(2\pi)^3} \frac{1}{2E_{\bm{p}}(\lambda)} |\lambda_{\bm{p}}\rangle\langle\lambda_{\bm{p}}|

我们接下来假设 x0>y0x^0>y^0，并且丢掉不感兴趣的常数项 ⟨Ω∣ϕ(x)∣Ω⟩⟨Ω∣ϕ(y)∣Ω⟩\langle\Omega| \phi(x)|\Omega\rangle\langle\Omega| \phi(y)|\Omega\rangle （这一项通常为零）。由此，两点关联函数成为：

⟨Ω∣ϕ(x)ϕ(y)∣Ω⟩=∑λ∫d3p(2π)312Ep(λ)⟨Ω∣ϕ(x)∣λp⟩⟨λp∣ϕ(y)∣Ω⟩(1)\langle\Omega|\phi(x)\phi(y)|\Omega\rangle = \sum_{\lambda}\int \frac{d^3p}{(2\pi)^3} \frac{1}{2E_{\bm{p}}(\lambda)}\langle\Omega| \phi(x)|\lambda_{\bm{p}}\rangle\langle\lambda_{\bm{p}}| \phi(y)|\Omega\rangle\tag{1}

我们可以如下处理矩阵元：

⟨Ω∣ϕ(x)∣λp⟩=⟨Ω∣eiP⋅xϕ(0)e−iP⋅x∣λp⟩=⟨Ω∣ϕ(0)∣λp⟩e−ip⋅x∣p0=Ep=⟨Ω∣ϕ(0)∣λ0⟩e−ip⋅x∣p0=Ep\begin{aligned} \langle\Omega|\phi(x)|\lambda_{\bm{p}}\rangle &= \langle\Omega| e^{iP\cdot x}\phi(0)e^{-iP\cdot x}|\lambda_{\bm{p}}\rangle\\ &= \langle\Omega|\phi(0)|\lambda_{\bm{p}}\rangle e^{-ip\cdot x}|_{p^0 = E_{\bm{p}}}\\ &= \langle\Omega|\phi(0)|\lambda_{0}\rangle e^{-ip\cdot x}|_{p^0 = E_{\bm{p}}}\\ \end{aligned}

最后一步运用了，ϕ(0)\phi(0) 与 Ω\Omega 在 boost 下的不变性。

将上述结果代入，再引入对 p0p^0 的积分，(1)(1) 式成为：

⟨Ω∣ϕ(x)ϕ(y)∣Ω⟩=∑λ∫d4p(2π)4ip2−mλ2+iϵe−ip⋅(x−y)∣⟨Ω∣ϕ(0)∣λ0⟩∣2=∫0∞dM22πρ(M2)DF(x−y;M2)(2)\begin{aligned} \langle \Omega|\phi(x)\phi(y)|\Omega\rangle &= \sum_{\lambda}\int \frac{d^4p}{(2\pi)^4} \frac{i}{p^2-m_{\lambda}^2 + i\epsilon}e^{-ip\cdot(x-y)}|\langle\Omega|\phi(0)|\lambda_0\rangle|^2\\ &= \int_{0}^{\infty} \frac{dM^2}{2\pi}\rho(M^2)D_F(x-y;M^2)\\ \end{aligned}\tag{2}

上式子第二行给出两点关联函数的 Kallen-Lehmann spectral representation。其中：

ρ(M2)=∑λ(2π)δ(M2−mλ2)∣⟨Ω∣ϕ(0)∣λ0⟩∣2(3)\rho(M^2) = \sum_{\lambda} (2\pi)\delta(M^2 - m_{\lambda}^2) |\langle\Omega|\phi(0)|\lambda_0\rangle|^2\tag{3}

称为 谱密度函数 spectral density function。

对于自由场的情形，不难得到：

ρ(M2)=2πδ(M2−m2)\rho(M^2) = 2\pi \delta(M^2-m^2)

即自由场中两点关联函数只会得到质量为 mm 的基态，而不会产生多粒子激发态。

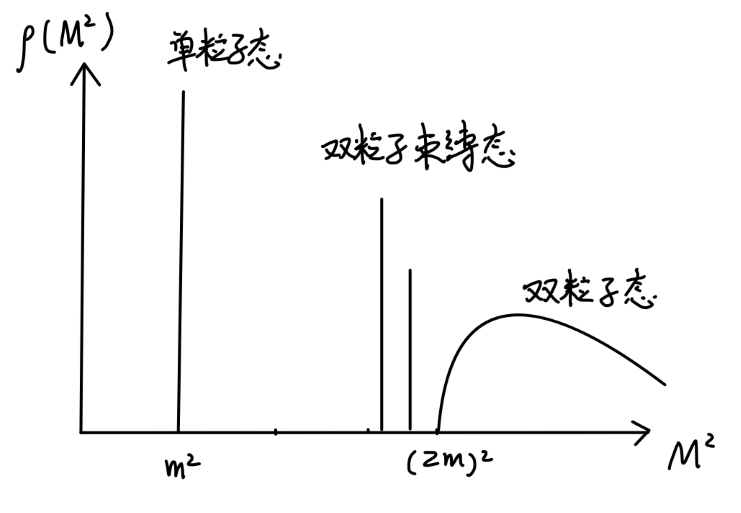
一个典型的谱密度有如下形式：

ρ(M2)=2πδ(M2−m2)⋅Z+(nothing else until M2≳(2m)2)\rho(M^2) = 2\pi \delta(M^2-m^2)\cdot Z + (nothing\ else\ until\ M^2 \gtrsim (2m)^2)

其中 ZZ 称为 场强重整化 field-strength renomalization。其中的质量 mm 就是静止粒子对应的哈密顿量本征值，是粒子的物理质量（这将与我们之后讨论的：在拉格朗日量中出现的 裸质量 m0m_0 相区分）。如何理解这个谱密度呢？首先，谱密度中出现的 δ\delta 函数对应于传播子的 极点，这表现为分立谱，例如质量为 mm 的单粒子态。在 M2≲(2m)2M^2\lesssim (2m)^2 时，两个粒子间由于存在相互作用，是可以产生一些束缚态的。在 M2≳(2m)2M^2\gtrsim (2m)^2 时，产生多粒子态，这对应于传播子的 branch cut。

那么两点关联函数成为：

∫d4xeip⋅x⟨Ω∣Tϕ(x)ϕ(0)∣Ω⟩=∫0∞dM22πρ(M2)ip2−M2+iϵ=iZp2−m2+iϵ+∫∼4m2∞dM22πρ(M2)ip2−M2+iϵ(4)\begin{aligned} \int d^4x e^{ip\cdot x}\langle\Omega|T\phi(x)\phi(0)|\Omega\rangle &= \int_{0}^{\infty} \frac{dM^2}{2\pi} \rho(M^2) \frac{i}{p^2-M^2+i\epsilon}\\ &=\frac{iZ}{p^2 - m^2 + i\epsilon} + \int_{\sim 4m^2}^{\infty} \frac{dM^2}{2\pi} \rho(M^2) \frac{i}{p^2-M^2+i\epsilon}\\ \end{aligned}\tag{4}

比较真空两点关联函数：

⟨0∣Tϕ(x)ϕ(0)∣0⟩=ip2−m2+iϵ\langle 0|T\phi(x)\phi(0)|0\rangle = \frac{i}{p^2-m^2+i\epsilon}

比较发现：一般的两点关联函数中包含场强重整化，且包含多粒子态的贡献。

对于 Dirac 场的两点关联函数。其具有以下结构

∫d4xeip⋅x⟨Ω∣Tψ(x)ψˉ(0)∣Ω⟩=iZ2∑sus(p)uˉs(p)p2−m2+iϵ+⋯=iZ2(p+m)p2−m2+iϵ+⋯\begin{aligned} \int d^4x e^{ip\cdot x}\langle\Omega|T\psi(x)\bar{\psi}(0)|\Omega\rangle &= \frac{iZ_2\sum_s u^s(p)\bar{u}^s(p)}{p^2-m^2+i\epsilon} + \cdots\\ &= \frac{iZ_2(\cancel{p}+m)}{p^2-m^2+i\epsilon} + \cdots\\ \end{aligned}

其中 Z2Z_2 是产生或湮灭一个单粒子态的概率：

⟨Ω∣ψ(0)∣p,s⟩=Z2us(p)\langle \Omega|\psi(0)|p,s\rangle = \sqrt{Z_2}u^s(p)

对应于 Dirac 场的场强重整化。

接下来我们来通过一个例子看看重整化的含义。

电子自能

根据微扰论，电子的两点关联函数 ⟨Ω∣Tψ(x)ψˉ(y)∣Ω⟩\langle \Omega| T\psi(x)\bar{\psi}(y)|\Omega\rangle 等价于如下费曼图的总和：

第一项对应于自由场的传播子：

ip+m0p2−m02+iϵ\frac{i\cancel{p}+m_0}{p^2-m_0^2 + i\epsilon}

对于第二个费曼图，我们称为 电子自能图，根据费曼规则，其值为：

i(p+m0)p2−m02[−iΣ2(p)]i(p+m0)p2−m02\frac{i(\cancel{p}+m_0)}{p^2-m_0^2}[-i\Sigma_2(p)]\frac{i(\cancel{p}+m_0)}{p^2-m_0^2}

其中：

−iΣ2(p)=(−ie)2∫d4k(2π)4γμi(k+m0)k2−m02+iϵγμ−i(p−k)2−μ2+iϵ-i\Sigma_2(p) = (-ie)^2 \int \frac{d^4k}{(2\pi)^4}\gamma^{\mu}\frac{i(\cancel{k}+m_0)}{k^2-m_0^2+i\epsilon} \gamma_{\mu} \frac{-i}{(p-k)^2 - \mu^2 +i\epsilon}

这里 Σ2\Sigma_2 指的是 ee 的二阶项（含有 e2e^2）对 Σ\Sigma 的贡献，其中我们为光子引入了一个小质量 μ\mu。通过费曼参数化，将上述积分中两个分母进行合并，即：

1k2−m02+iϵ1k2−μ2+iϵ=∫01dx1[k2−2xk⋅p+xp2−xμ2−(1−x)m02+iϵ]2\frac{1}{k^2-m_0^2 + i\epsilon}\frac{1}{k^2-\mu^2 + i\epsilon} = \int_{0}^{1}dx \frac{1}{[k^2 - 2xk\cdot p +xp^2 -x\mu^2 -(1-x)m_0^2 + i\epsilon]^2}

如此可以得到：

−iΣ2(p)=−e2∫01dx∫d4l(2π)4−2xp+4m0(l2−Δ+iϵ)-i\Sigma_2(p) = -e^2 \int_{0}^{1}dx\int \frac{d^4l}{(2\pi)^4} \frac{-2x\cancel{p} + 4m_0}{(l^2-\Delta + i\epsilon)}

其中：

l≡k−xpΔ=−x(1−x)p2+xμ2+(1−x)m02l \equiv k-xp\quad \Delta = -x(1-x)p^2 + x\mu^2 + (1-x)m_0^2

为了解决紫外发散，我们使用 Pauli-Villars 正规化：

1(k−p)2−μ2+iϵ→1(p−k)2−μ2+iϵ−1(p−k)2−Λ2+iϵ\frac{1}{(k-p)^2 - \mu^2 +i\epsilon} \rightarrow \frac{1}{(p-k)^2 - \mu^2 + i\epsilon} - \frac{1}{(p-k)^2 - \Lambda^2 + i\epsilon}

紧接着做 wick rotation，计算对 d4ld^4l 的积分，得到：

Σ2=α2π∫01dx(2m0−xp)log⁡(xΛ2(1−x)m02+xμ2−x(1−x)p2)(5)\Sigma_2 = \frac{\alpha}{2\pi} \int_{0}^{1}dx(2m_0-x\cancel{p})\log (\frac{x\Lambda^2}{(1-x)m_0^2 + x\mu^2 -x(1-x)p^2})\tag{5}

我们首先考虑分母的行为，令分母为零，得到：

(1−x)m02+xμ2−x(1−x)p2=0(1-x)m_0^2 + x\mu^2 -x(1-x)p^2 = 0

解得：

x=12+m022p2−μ22p2±12p2[p2−(m0+μ)2][p2−(m0−μ)2]x = \frac{1}{2} + \frac{m_0^2}{2p^2} - \frac{\mu^2}{2p^2} \pm \frac{1}{2p^2}\sqrt{[p^2-(m_0+\mu)^2][p^2-(m_0-\mu)^2]}

当 p2⩾(m0+μ)2p^2 \geqslant (m_0+\mu)^2 时，我们得到两个解 x∈[0,1]x\in[0,1]。此时是存在 branch cut 的。这对应产生一个电子加一个光子的两粒子态。

下面，我们定义 不可约单粒子图 one-particle irreducible(1PI)：它们是那些“不能够通过去掉单个的连线成为两个图”的图。

例如：

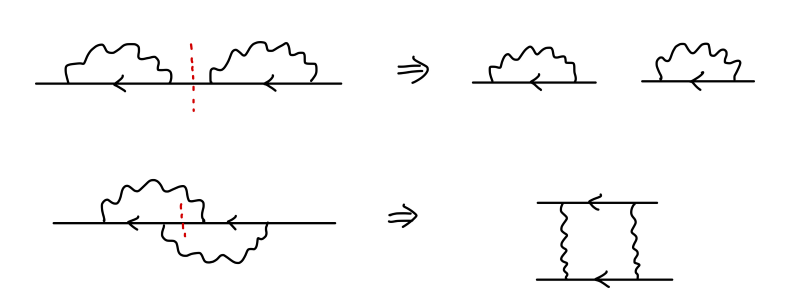
其中上面的图为可约图，下面的图为不可约图。

我们令 −iΣ(p)-i\Sigma(p) 代表所有具有两个外部费米子线的 1PI 图的值。

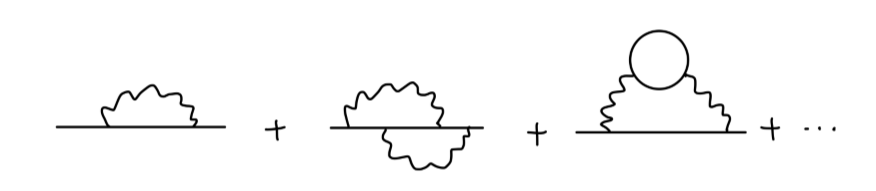
我们将 1PI 图表示为：

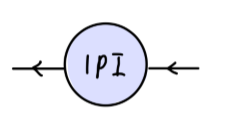
那么关联函数实际上是多个 1PI 图的总和：

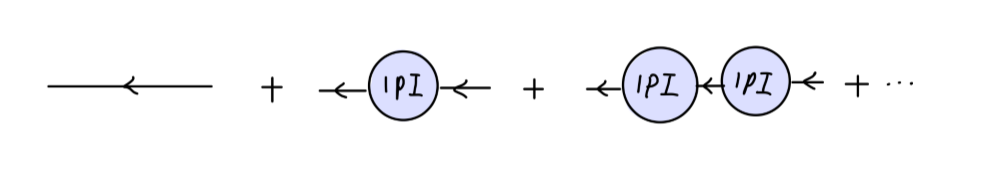
即：

∫d4x⟨Ω∣Tψ(x)ψˉ(0)∣Ω⟩eip⋅x=i(p+m0)p2−m02+i(p+m0)p2−m02(−iΣ)i(p+m0)p2−m02+⋯=ip−m0+ip−m0(Σ(p)p−m0)+ip−m0(Σ(p)p−m0)2+⋯=ip−m0−Σ(p)(6)\begin{aligned} &\int d^4x \langle\Omega|T\psi(x)\bar{\psi}(0)|\Omega\rangle e^{ip\cdot x}\\ &= \frac{i(\cancel{p}+m_0)}{p^2-m_0^2} + \frac{i(\cancel{p}+m_0)}{p^2-m_0^2}(-i\Sigma)\frac{i(\cancel{p}+m_0)}{p^2-m_0^2} + \cdots\\ &= \frac{i}{\cancel{p}-m_0} + \frac{i}{\cancel{p}-m_0} (\frac{\Sigma(\cancel{p})}{\cancel{p}-m_0}) + \frac{i}{\cancel{p}-m_0} (\frac{\Sigma(\cancel{p})}{\cancel{p}-m_0})^2 + \cdots \\ &= \frac{i}{\cancel{p} - m_0 - \Sigma(\cancel{p})} \end{aligned}\tag{6}

考虑上式极点对应于物理质量 mm，即：

[p−m0−Σ(p)]∣p=m=0(7)[\cancel{p} -m_0 - \Sigma(\cancel{p})]|_{\cancel{p} = m} = 0\tag{7}

在极点附近，上述分母可以展开为：

(p−m)⋅(1−dΣdp∣p=m)+O((p−m)2)(\cancel{p}-m)\cdot(1-\frac{d\Sigma}{d\cancel{p}}|_{\cancel{p} = m}) + \mathcal{O}((\cancel{p}-m)^2)

由此得到：

Z2−1=1−dΣdp∣p=m(8)Z_2^{-1} = 1-\frac{d\Sigma}{d\cancel{p}}|_{\cancel{p} = m}\tag{8}

由此，质量修正为：

δm=m−m0=Σ2(p=m)≈Σ2(p=m0)\delta m = m - m_0 = \Sigma_2(\cancel{p}=m) \approx \Sigma_2(\cancel{p}=m_0)

那么代入公式 (5)(5) 得到：

δm=α2πm0∫01dx(2−x)log⁡(xΛ2(1−x)2m02+xμ2)→Λ→∞3α4πm0log⁡(Λ2m02)(9)\begin{aligned} \delta m &= \frac{\alpha}{2\pi}m_0 \int_{0}^{1}dx(2-x)\log (\frac{x\Lambda^2}{(1-x)^2m_0^2 + x\mu^2})\\ &\underset{\Lambda\rightarrow\infty}{\rightarrow} \frac{3\alpha}{4\pi}m_0 \log (\frac{\Lambda^2}{m_0^2})\\ \end{aligned}\tag{9}

那么如何解释 (9)(9) 式中出现的 δm→∞\delta m \rightarrow \infty 呢？首先我们要说明：我们不可能测得电子得裸质量，电子一定是与电磁场耦合在一起的。我们测量得到的，当然是考虑电子自能后的物理质量 mm。当 m0=0m_0 = 0 时，ψL\psi_L 与 ψR\psi_R 是解耦的，同电磁场耦合不会产生质量项。因此质量修正 δm\delta m 将于 m0m_0 成正比。即使质量修正出现无穷大的项，这并不影响我们的计算。在考虑 α\alpha 阶修正时，我们只需要将本来的裸质量 m0m_0 替换成物理质量 mm 即可。

得到对 Z2Z_2 的修正为：

δZ2=Z2−1=dΣ2dp∣p=m=α2π∫01dx[−xlog⁡xΛ2(1−x)2m2+xμ2+2(2−x)x(1−x)m2(1−x)2m2+xμ2]\begin{aligned} \delta Z_2 &= Z_2 - 1\\ &= \frac{d\Sigma_2}{d\cancel{p}}|_{\cancel{p}=m}\\ &= \frac{\alpha}{2\pi}\int_{0}^{1}dx[-x\log \frac{x\Lambda^2}{(1-x)^2m^2+x\mu^2} + 2(2-x)\frac{x(1-x)m^2}{(1-x)^2m^2+x\mu^2}] \end{aligned}

考虑我们之前得到对 δF1(0)\delta F_1(0) 的修正：

δF1(0)=α2π∫01dxdydzδ(x+y+z−1)×[log⁡(zΛ2(1−z)2m2+zμ2)+(1−4z+z2)m2(1−z)2m2+zμ2]=α2π∫01dz(1−z)(log⁡(zΛ2(1−z)2m2+zμ2)+(1−4z+z2)m2(1−z)2m2+zμ2)\begin{aligned} \delta F_1(0) &= \frac{\alpha}{2\pi}\int_{0}^{1}dxdydz\delta(x+y+z-1)\\ &\quad \times [\log(\frac{z\Lambda^2}{(1-z)^2m^2+z\mu^2}) + \frac{(1-4z+z^2)m^2}{(1-z)^2m^2 + z\mu^2}]\\ &= \frac{\alpha}{2\pi}\int_{0}^{1}dz(1-z)(\log(\frac{z\Lambda^2}{(1-z)^2m^2+z\mu^2}) + \frac{(1-4z+z^2)m^2}{(1-z)^2m^2 + z\mu^2}) \end{aligned}

通过分部积分可以计算下列表达式：

∫01dz(1−2z)log⁡(Λ2(1−z)2m2+zμ2)=−∫01dzz(1−z)2(1−z)m2−μ2(1−z)2m2+zμ2=∫01dz[(1−z)−(1−z)(1−z2)m2(1−z)2m2+zμ2]\begin{aligned} \int_{0}^{1}dz(1-2z)\log(\frac{\Lambda^2}{(1-z)^2m^2+z\mu^2}) &= -\int_{0}^{1}dz z(1-z)\frac{2(1-z)m^2-\mu^2}{(1-z)^2m^2 + z\mu^2}\\ &= \int_{0}^{1}dz[(1-z) - \frac{(1-z)(1-z^2)m^2}{(1-z)^2m^2+z\mu^2}]\\ \end{aligned}

因此得到：

δF1(0)+δZ2=α2π∫01dz[(1−2z)log⁡Λ2(1−z)2m2+zμ2+(1−2z)log⁡z+2(2−z)z(1−z)m2(1−z)2m2+zμ2+(1−4z+z2)m2(1−z)2m2+zμ2]=α2π∫01dz[(1−z)−(1−z)(1−z2)m2(1−z)2m2+zμ2]+(1−2z)log⁡z+2(2−z)z(1−z)m2(1−z)2m2+zμ2+(1−4z+z2)m2(1−z)2m2+zμ2]=α2π∫01dz(1−z+(1−2z)log⁡z)=α2π(z−z2)log⁡z∣01=0\begin{aligned} \delta F_1(0) + \delta Z_2=&\frac{\alpha}{2\pi}\int_{0}^{1}dz[(1-2z)\log \frac{\Lambda^2}{(1-z)^2m^2+z\mu^2}+ (1-2z)\log z\\ &\quad + 2(2-z)\frac{z(1-z)m^2}{(1-z)^2m^2+z\mu^2} + \frac{(1-4z+z^2)m^2}{(1-z)^2m^2 + z\mu^2}]\\ &= \frac{\alpha}{2\pi}\int_{0}^{1}dz [(1-z) - \frac{(1-z)(1-z^2)m^2}{(1-z)^2m^2+z\mu^2}] + (1-2z)\log z\\ &\quad + 2(2-z)\frac{z(1-z)m^2}{(1-z)^2m^2+z\mu^2} + \frac{(1-4z+z^2)m^2}{(1-z)^2m^2 + z\mu^2}]\\ &=\frac{\alpha}{2\pi}\int_{0}^{1}dz(1-z + (1-2z)\log z)\\ &=\frac{\alpha}{2\pi} (z-z^2)\log z|_{0}^{1} = 0\\ \end{aligned}

即：

δF1(0)+δZ2=0(10)\delta F_1(0) + \delta Z_2=0\tag{10}

在这里，我们解决了一个疑问。在上一篇中，对形状因子的顶点修正是发散的，因此我们使用了 δF1(q2)−δF1(0)\delta F_1(q^2) -\delta F_1(0) 来代替 δF1(0)\delta F_1(0) 以保证 F1(q2)F_1(q^2) 在 q2=0q^2 = 0 的取值为 11。那么现在考虑场强重整化后，对一个跃迁矩阵元的修正成为：

γμ→γμF1(q2)Z2≈γμ(1+δF1(q2)+δZ2)=γμ(1+δF1(q2)−δF1(0))\begin{aligned} \gamma^{\mu} \rightarrow \gamma^{\mu}F_1(q^2)Z_2 &\approx \gamma^{\mu}(1 + \delta F_1(q^2) + \delta Z_2)\\ &= \gamma^{\mu}(1+\delta F_1(q^2) - \delta F_1(0)) \\ \end{aligned}

这正是我们在上一篇中的做法。