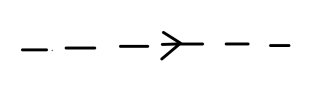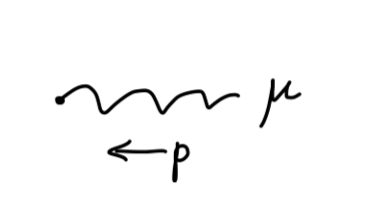费米子的费曼规则
首先为了应用 wick 定理,我们需要将时序符号进行推广,对于费米子场量 ψ(x) 来说:
T(ψ(x)ψˉ(y))≡{−ψ(x)ψˉ(y)ψˉ(y)ψ(x)x0>y0x0<y0(1)
那么 Dirac 场的费米传播子可以表示为:
SF(x−y)=∫(2π)4d4pp2−m2+iϵi(p+m)e−ip⋅(x−y)=⟨0∣Tψ(x)ψˉ(y)∣0⟩(2)
同样的,我们要推广正规序。注意,此时由于 Dirac 场阶梯算子的反对易关系,存在多种不同的正规序表示方式。例如:
N(apaqar†)=(−1)2ar†apaq=(−1)3ar†aqap(3)
每一次相邻的阶梯算子的置换需要添加一个负号。
对于 Dirac 场来说,其中:
ψ+(x)ψ−(x)ψˉ+(x)ψˉ−(x)=∫(2π)3d3p2Ep1s∑apsus(p)e−ip⋅x=∫(2π)3d3p2Ep1s∑bps†vs(p)eip⋅x=∫(2π)3d3p2Ep1s∑bpsvˉs(p)e−ip⋅x=∫(2π)3d3p2Ep1s∑aps†uˉs(p)eip⋅x(4)
对于 x0>y0 的情况:
T(ψ(x)ψˉ(y))=x0>y0ψ+(x)ψˉ+(y)+ψ+(x)ψˉ−(y)+ψ−(x)ψˉ+(y)+ψ−(x)ψˉ−(y)(5)
而:
N(ψ(x)ψˉ(y))=ψ+(x)ψˉ+(y)−ψˉ−(y)ψ+(x)+ψˉ+(y)ψ−(x)+ψ−(x)ψˉ−(y)(6)
对比得到:
T(ψ(x)ψˉ(y))=x0>y0N(ψ(x)ψˉ(y))+{ψ+(x),ψˉ−(y)}
类似的,对于 x0<y0 的情况,可以得到:
T(ψ(x)ψˉ(y))=x0<y0N(ψ(x)ψˉ(y))−{ψˉ+(y),ψ−(x)}
这样,我们定义费米子场间的缩并:
ψ∙(x)ψˉ∙(y)={−{ψ+(x),ψˉ−(y)}{ψˉ+(y),ψ−(x)}x0>y0x0<y0(7)
其值正是 Dirac 场传播子,见 量子场论笔记(七):Dirac 场的量子化。
ψ∙(x)ψˉ∙(y)=SF(x−y)(8)
那么有:
T(ψ(x)ψˉ(y))=N(ψ(x)ψˉ(y))+ψ∙(x)ψˉ∙(y)(9)
对于 ψ,ψ 或者 ψˉ,ψˉ 间的缩并,不难得到:
ψ∙(x)ψ∙(y)=ψˉ∙(x)ψˉ∙(y)=0(10)
在进行缩并计算时,我们需要考虑符号,例如:
N(ψ1∙ψ2ψˉ3∙ψˉ4)=−ψ1∙ψ3∙N(ψ2ψˉ4)=−SF(x1−x3)N(ψ2ψˉ4)
对于费米子来说,我们同样也有 wick 定理:
T[ψ1ψˉ2ψ3⋯]=N[ψ1ψˉ2ψ3⋯+ all possible contractions](11)
Yukawa 理论
我们现在分析 Yukawa 理论 的散射过程,Yukawa 理论是一个 量子电动力学 Quantum Electrodynamics(QED) 的简化模型,我们这里的讨论将为之后的 QED 做铺垫。Yukawa 理论的哈密顿量写为:
H=HDirac+HKlein−Gordon+∫d3xgψˉψϕ(12)
其中 HDirac,HKlein−Gordon 分别为自由 Dirac 场与 Klein-Gordon 场的哈密顿量,而第三项将这两个场耦合起来,表示相互作用,我们将这一项看成微扰。
我们现在考虑如下的两个费米子的散射过程:
fermion(p)+fermion(k)→fermion(p′)+fermion(k′)
对散射矩阵的主要贡献项是二阶项:
⟨p′,k′∣T{2!1(−ig)∫d4xψˉIψIϕI(−ig)∫d4yψˉIψIϕI}∣p,k⟩(13)
之前我们已经讨论了:费米子场之间的缩并、玻色子场之间的缩并。由于在该过程中:初态/末态均为费米子,那么玻色子场不能与费米子的初态/末态发生缩并,那么费米子场能不能与费米子的初态/末态发生缩并呢?答案是肯定的。
我们需要去区分初态/末态粒子为正粒子或是反粒子。
对于正粒子有:
ψ+(x)∣p,s⟩⟨p,s∣ψˉ−(x)=∫(2π)3d3q2Eq1r∑aqrur(q)e−iq⋅x2Epaps†∣0⟩=∫(2π)3d3q2Eq1r∑ur(q)e−iq⋅x2Ep(2π)3δrsδ(3)(p−q)∣0⟩=e−ip⋅xus(p)∣0⟩=⟨0∣uˉs(p)eip⋅x
对于反粒子来说:
∣k,s⟩=2Ekbks∣0⟩
类似得到:
ψˉ+(x)∣k,s⟩⟨k,s∣ψ−(x)=e−ik⋅xvˉs(k)∣0⟩=⟨0∣vs(k)eik⋅x
于是我们可以定义费米子场与费米子初态/末态间的缩并:
ψ∙(x)fermion∣p,s∙⟩fermion⟨p,s∙∣ψˉ∙(x)ψˉ∙(x)antifermion∣k,s∙⟩antifermion⟨k,s∙∣ψ∙(x)=e−ip⋅xus(p)∣0⟩=⟨0∣uˉs(p)eip⋅x=e−ik⋅xvˉs(k)∣0⟩=⟨0∣vs(k)eik⋅x(14)
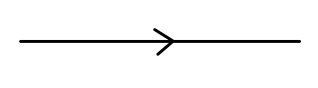
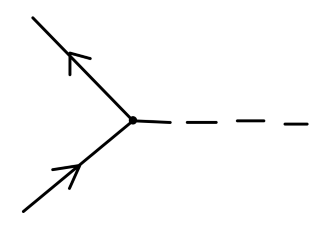
以及对应的费曼图:
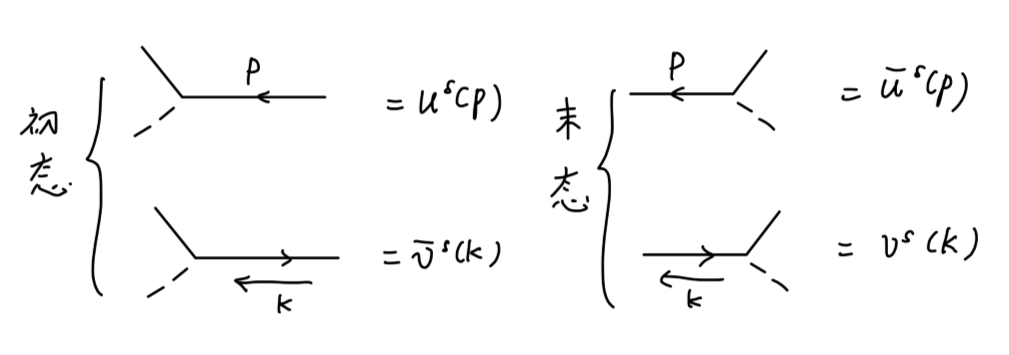
注意此时:实线代表费米子,费米子线上的箭头不再代表动量方向。我们规定:箭头沿着时间方向代表正粒子、箭头逆着时间方向代表反粒子。
Fig:费米子
现在我们可以计算 (13) 式,其为以下缩并的贡献。考虑两个顶点的对称性,存在两种等价的缩并方式
⟨p′∙,k′∙∙∣2!1(−ig)∫d4xψˉI∙ψI⋆ϕI(3∙)(−ig)∫d4yψˉI∙∙ψI⋆⋆ϕI(3∙)∣p⋆,k⋆⋆⟩
费曼图为:
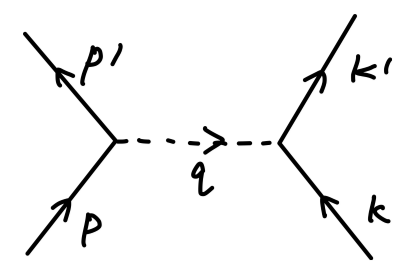
其中虚线对应 Klein-Gordon 玻色子。
其值为:
(−ig)2∫(2π)4d4qq2−mϕ2i(2π)4δ(p′−p−q)(2π)4δ(k′−k+q)uˉ(p′)u(p)uˉ(k′)u(k)
其中 mϕ 为 Klein-Gordon 玻色子的质量。
我们现在来推导动量空间中的费曼规则。我们采取类似的做法:对于可能出现的 Klein-Gordon 传播子:
DF(x−y)=∫(2π)4d4pp2−mϕ2+iϵie−ip⋅(x−y)
或是 Dirac 传播子:
SF(x−y)=∫(2π)4d4pp2−m2+iϵi(p+m)e−ip⋅(x−y)
我们将 e−ipx,eipy 因子与相应的顶点关联起来。对于每个顶点,我们需要作积分,其结果为保证四动量守恒的 δ 函数与耦合常数 −ig 的乘积。对于每个外部线,我们也将 e−ip⋅x 与顶点关联起来,保留旋量场 u(p) 等。最后,我们要对所有未确定的动量进行积分。
另外还要说明两点:
-
对于 n 阶修正中的 1/n! 因子,总可以通过对 n 个顶点进行置换消去。
-
Yukawa 理论对应的费曼图的对称因子 S=1,因为每个顶点由 ψˉψϕ 组成,是不具有对称性的。
我们总结得到 Yukawa 理论动量空间的费曼规则为:
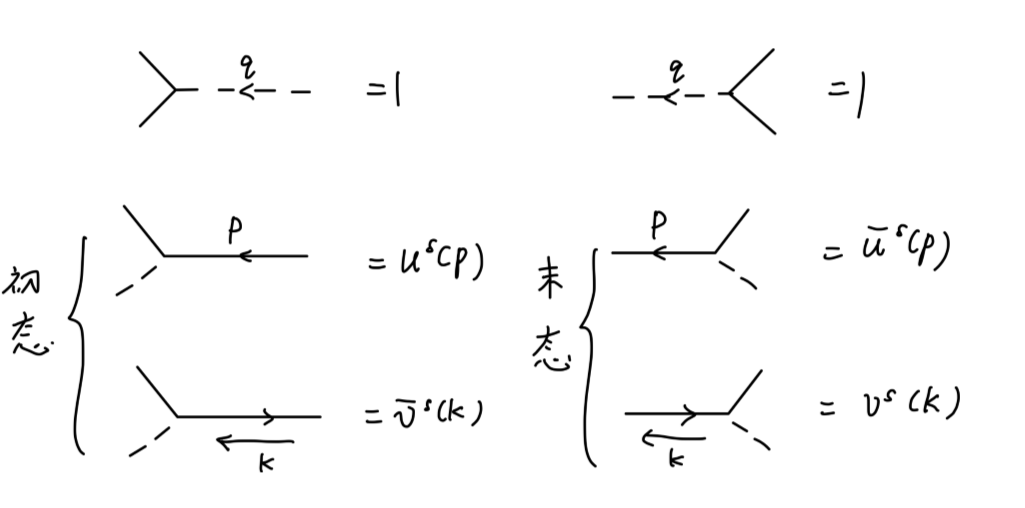
∫(2π)4d4p
现在我们来讨论以下最后一点:图的符号。对于多个粒子构成初态与末态来说,我们习惯取:
∣p,k⟩∼ap†ak†∣0⟩,⟨p′,k′∣∼⟨0∣ak′ap′
这里的阶梯算子的顺序是关键的,如此有:∣p,k⟩†=⟨p,k∣
那么考虑两个全同费米子的散射的领头阶:
⟨p′,k′∣(ψˉψ)x(ψˉψ)y∣p,k⟩
存在两种不等价的缩并方式:
这里的玻色子场,耦合常数,积分等元素暂时略去了。我们重点关注费米子场的缩并。
⟨p′∙,k′∙∙∣(ψˉ∙∙ψ⋆⋆)x(ψˉ∙ψ⋆)y∣p⋆,k⋆⋆⟩⟨p′∙,k′∙∙∣(ψˉ∙ψ⋆⋆)x(ψˉ∙∙ψ⋆)y∣p⋆,k⋆⋆⟩
它们的值相差一个负号。对应的费曼图分别为:
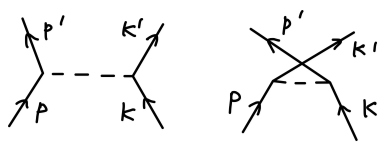
它们对全同费米子的散射都有贡献。
iM=(−ig2)[uˉ(p′)u(p)(p′−p)2−mϕ21uˉ(k′)u(k)−uˉ(p′)u(k)(p−k′)2−mϕ21uˉ(k′)u(p)]
对于一些较为复杂的情形,我们常常将 ψˉψ 组合在一起考虑以简化计算。例如:
==⋯(ψˉψ∙)x(ψˉ∙∙ψ⋆)y(ψˉ∙ψ∙∙)z(ψˉ⋆ψ)w⋯⋯(+1)(ψˉψ∙)x(ψˉ∙ψ∙∙)z(ψˉ∙∙ψ⋆)y(ψˉ⋆ψ)w⋯⋯SF(x−z)SF(z−y)SF(y−w)⋯
对于如下圈图:
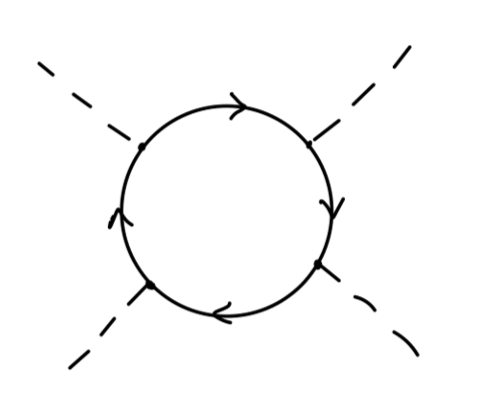
其值为:
==ψˉ⋆⋆ψ∙ ψˉ∙ψ∙∙ ψˉ∙∙ψ⋆ ψˉ⋆ψ⋆⋆−tr[ψ⋆⋆ψˉ⋆⋆ψ∙ ψˉ∙ψ∙∙ ψˉ∙∙ψ⋆ ψˉ⋆]−tr[SFSFSFSF](15)
Yukawa 势
我们现在在非相对论极限下对上述散射的计算做一些估计。我们此时只保留含有三维动量的最低阶项。有:
p=(m,p)p′=(m,p′)k=(m,k)k′=(m,k′)
以及:
(p′−p)2=−∣p′−p∣2+O(p4)us(p)=m(ξsξs)
旋量积具有如下关系:
uˉs′(p′)us(p)=2mξs′†ξs=2mδss′uˉr′(p′)ur(p)=2mξr′†ξr=2mδrr′
那么对应的跃迁矩阵元成为:
iM==(−ig2)uˉ(p′)u(p)(p′−p)2−mϕ21uˉ(k′)u(k)∣p′−p∣2+mϕ2ig22mδss′2mδrr′(16)
在非相对论量子力学中,我们利用 Born 近似可以写出跃迁矩阵元:
⟨p′∣iT∣p⟩=−iV~(q)(2π)δ(Ep′−Ep)q=p′−p(17)
比较 (16)(17) 式,我们得到 Yukawa 相互作用的势函数形式为:
V~(q)=∣q∣2+mϕ2−g2(18)
变换到坐标空间,得到:
V(r)=−4πg2r1e−mϕr(19)
这就是 Yukawa 势 Yukawa potential。
QED
下面我们从 Yuakawa 理论过渡到 QED(Quantum Electrodynamics)。此时只需要将 Yukawa 相互作用项中的标量场 ϕ 替换为矢量场 Aμ 即可:
Hint=∫d3xeψˉγμψAμ(20)
我们考虑矢势的洛伦兹规范:
∂2Aμ=0(21)
那么实际上 Aμ 满足无质量 Klein-Gordon 方程,类似的,可以将电磁场量子化:
Aμ(x)=∫(2π)3d3p2Ep1r=0∑3(aprϵμr(p)e−ip⋅x+apr†ϵμr∗(p)eip⋅x)(22)
QED 的费曼规则我们不作证明,但它们的形式是容易理解的。我们现在需要补充有关电磁场的矢量玻色子——光子的有关费曼规则:
-
光子传播子

值为:
q2+iϵ−gμν
-
顶点

值为:
−ieγμ
-
外部光子线
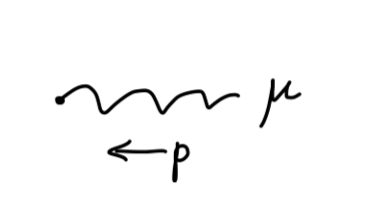
值为:
Aμ∙∣p∙⟩=ϵμ(p)

值为:
⟨p∙∣Aμ∙=ϵμ∗(p)
其中 ϵμ(p) 为光子的极化矢量。
类似 Yukawa 势,可以推导得到非相对论极限下 库伦势 Coulomb Potential的表达式:
V(r)=4πre2