广义相对论的数学基础（十）：流形

拓扑流形

流形 (manifold)
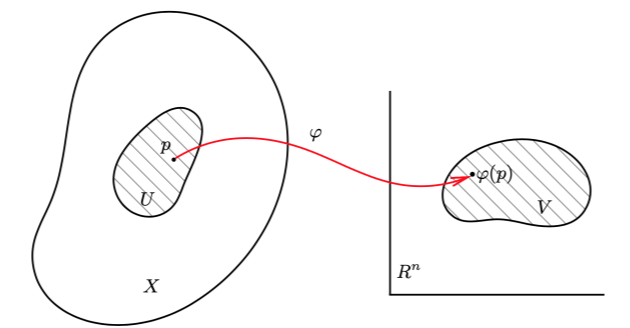
设 $X$ 是一个 Hausdorff 拓扑空间， $\forall p\in X$ ，都有 $p$ 的一个邻域 $N(p)$ 同胚于 $\mathbb{R}^n$ 中的某个开集。则称 $X$ 为一个 $n$ -维的拓扑流形（或简称流形）。

流形局部像欧式空间

坐标卡 (chart)
流形 $X$ 上的坐标卡是一个二元组 $(U,\varphi)$ ，其中 $U$ 是 $X$ 的开集，称为坐标卡的定义域； $\varphi$ 是一个从 $U$ 到 $\mathbb{R}^n$ 上某个开集 $V$ 的同胚： $\varphi: U \rightarrow V$ 。有时也称其为局部坐标系。

设 $p \in U$ ，则 $\varphi(p) \in V \subset \mathbb{R}^n$ 。在 $\mathbb{R}^ n$ 中 $\varphi(p)$ 可以用一组数

$(x^1 (p),\cdots ,x^ n (p))$

表示。这组数称为点 $p$ 在坐标卡 $(U,\varphi)$ 中的坐标 (coordinates)。有时候，人们称 $x^i$ 是坐标函数。它们是 $\mathbb{R}^n$ 上的一组映射：

$\begin{aligned} &x^i : \mathbb{R}^n \rightarrow \mathbb{R}\\ &u \mapsto x^i (u) = (u)^i ,\ \forall u \in \mathbb{R}^n \end{aligned}$

坐标函数 $x^i$ 的作用是：对 $\mathbb{R}^n$ 中的任意一点 $u$ ，给出它的第 $i$ 个坐标 $(u)^i$ 。 $x^i (p)$ 是 $x^i\circ \varphi(p)$ 的简写。比较细致地，我们可以定义复合映射：

$x_\varphi^i=x^i\circ \varphi:\quad p\mapsto x_\varphi^i(p)=(\varphi(p))^i$

对于每一个 $p$ ，给出它在坐标卡 $(U,\varphi)$ 下的坐标 $x^i_\varphi (p)$ （或 $x^i_U (p)$ ）。用下标 $\varphi$ (或 $U$ ) 可以明确的指出 $x^i_\varphi$ (或 $x^i_U$ )是坐标卡 $(U,\varphi)$ 下的坐标函数。 $x_{\varphi}^i$ 的作用是：对于每一个 $p$ ，给出它在坐标卡 $(U,\varphi)$ 下的坐标

微分流形

坐标卡集与微分结构

流形 $X$ 上的 $C^k$ 类 坐标卡集 (altas) 是流形 $X$ 上的坐标卡的集合 $\{(U_\alpha ,\varphi_\alpha )\}$ ，并要求这些坐标卡满足下面条件：

$\{U_\alpha \}$ 是 $X$ 的一个覆盖
相容性条件
由同胚 $\varphi_ \alpha$ 给出的映射

$\varphi_\beta \circ \varphi^{-1}_\alpha: \varphi _\alpha (U_ \alpha \cap U_\beta ) \rightarrow \varphi_{\beta} (U_{\alpha} \cap U_{\beta} )$

是 $\mathbb{R}^n$ 中开集与开集间的 $C^k$ 类（同胚）映射，即：

$x^i \mapsto y^i = y^i (x_1 ,\cdots ,x_n )$

是 $n$ 个 $C^k$ 类函数。这时，我们称这两个坐标卡是 $C^k$ -相容的。

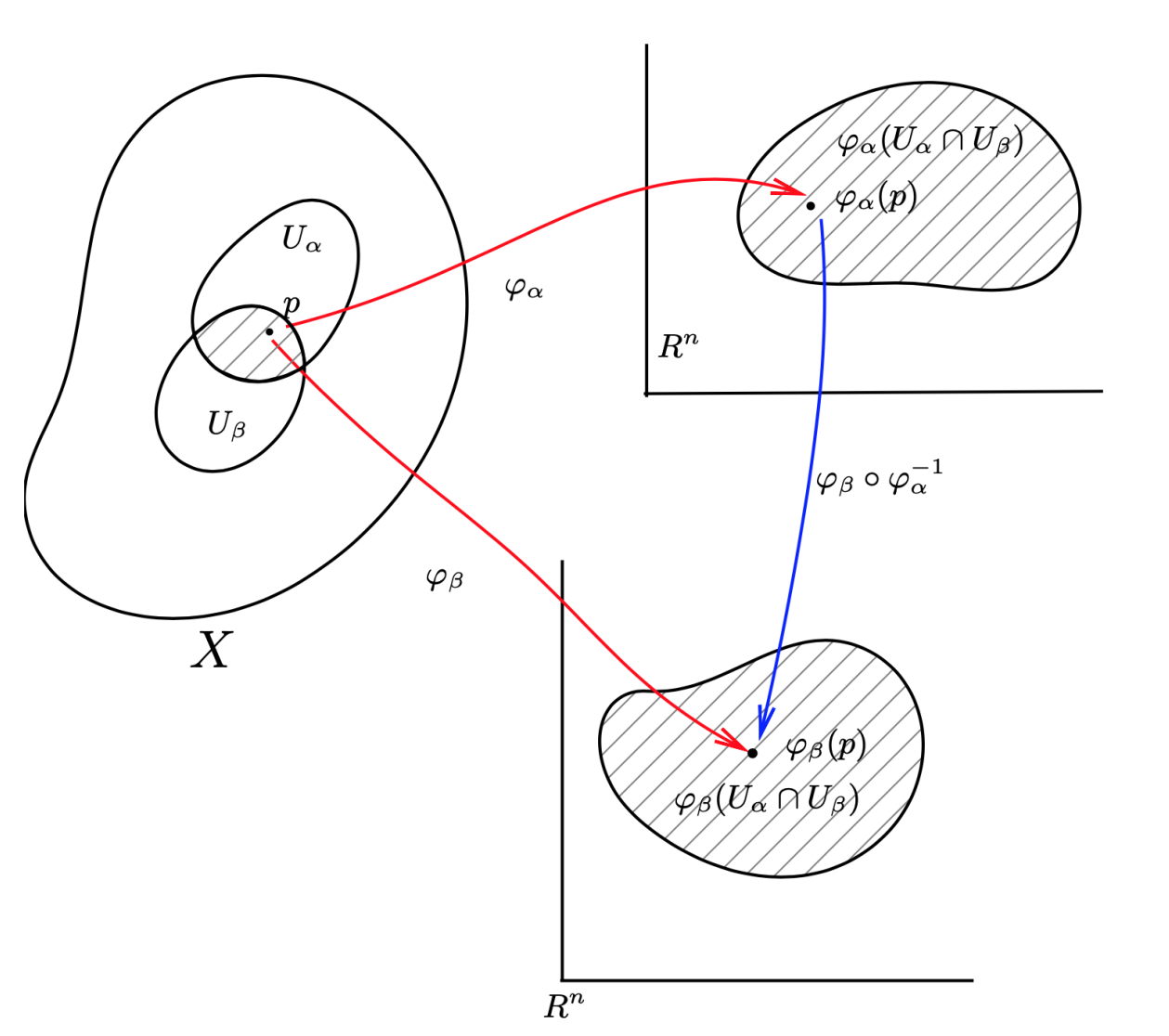
两个 $C^k$ 类坐标卡集称为是等价的，若它们的合并还是一个 $C^k$ 类的坐标卡集。即： $\{U_\alpha ,U_{\alpha'} \}$ 形成一个新的坐标卡定义域，而 $\{\phi_\alpha ,\phi_{\alpha'}\}$ 是相应的同胚。并要求这个新的坐标卡集也是 $C^k$ 类的。利用这种等价关系可以给出 微分结构 的概念。按上述等价关系，可以得到所有 $C^k$ 类坐标卡集的等价类。而这个等价类便称为一个 $C^k$ 类微分结构。

例：
极大坐标卡集
设 $X$ 是一个 $n-$ 维流形， $\mathscr{A} = \{(U_{\alpha} ,\varphi_{\alpha} )\}$ 是它的一个坐标卡集，并满足下面条件：

$\{U_\alpha \}$ 是 $X$ 的一个开覆盖；

$\mathscr{A}$ 中的任意两个坐标卡是 $C^k$ -相容的；

$\mathscr{A}$ 是极大的，即若 $(U,\varphi)$ 是 $X$ 的任一个坐标卡且和 $\mathscr{A}$ 中每个坐标卡都是 $C^k$ -相容，那么它必然属于 $\mathscr{A}$ 。

极大坐标集构成一个微分结构。

微分流形

对于拓扑流形 $X$ ，赋予其一个 $C^k$ 类微分结构，便称为一个 $C^k$ 类 微分流形。若要求对考虑的问题， $k$ 足够大 (以后我们遇到的通常是这种情况)，即 $C^{\infty}$ 类微分流形，又被称为 光滑流形。

一个拓扑流形可以赋予不同的微分结构，得到不同的微分流形。实微分流形是在局部上以 $\mathbb{R}^n$ 为模板得到的不同微分流形。

实解析流形 (real analytic)
也记为 $C^\omega$ 类微分流形. 要求函数 $\varphi_{\beta}\circ \phi^{-1}_\alpha$ 是实解析的.

复解析流形 (real analytic)
要求函数 $\varphi_{\beta}\circ \varphi^{-1}_\alpha$ 是全纯的 (holomorphic)或复解析的。

直积流形

我们可以从拓扑流形 $X^n$ 与 $Y^m$ 上出发构造直积流形。设它们的拓扑分别为 $\mathscr{U}_{X}$ 和 $\mathscr{U}_Y$ ，我们可以赋予直积流形 $Z^{n+m} = X^n \times Y^m$ 乘积拓扑。

对于拓扑流形 $X^n$ 与 $Y_m$ ，我们可以分别在其上引入微分结构及其相应的坐标卡集 $\{(U_X,\varphi_X)\}$ 和 $\{(U_Y,\varphi_Y)\}$ ，这样 $X^n$ 和 $Y^m$ 成为两个微分流形。

由坐标卡集 $\{(U_{X},\varphi_X)\}$ 和 $\{(U_{Y},\varphi_Y)\}$ ，我们可以构造 $Z^{n+m}$ 的坐标卡集 $(U_Z,\varphi_Z)$ ：该坐标卡的定义域为 $U_Z = U_X \times U_Y$ ，而相应的映射 $\varphi_Z$ 定义为：

$\varphi_Z(p,q) = (\varphi_X(p),\varphi_Y(q)),\quad \forall\ (p,q)\in U_Z$

这样 $Z^{n+m}$ 上便有了一个微分结构，这样构造出来的微分流形 $Z^{n+m}$ 称为 $X^n$ 和 $Y^m$ 的直积流形。

可微映射

可微函数

可微函数 (differentiable)
微分流形上的函数 $f$ 在点 $p$ 称为是可微的，如果在点 $p$ 的某个坐标卡 $(U,\varphi)$ ，函数

$F = f \circ \varphi^{-1}$

在 $\varphi(p)$ 是可微的。

这个定义不依赖于坐标卡的选取：若 $f\circ \varphi^{-1}$ 在 $\varphi(p)$ 可微，则在 $p$ 的任意一个坐标卡 $(\tilde{U},\tilde{\varphi})$ 在 $\tilde{\varphi}(p)$ 也是可微的，这是由于：

$f\circ \tilde{\varphi}^{-1} = (f\circ \varphi^{-1})\circ (\varphi\circ \tilde{\varphi}^{-1})$

也是可微的。

$r$ 阶可微函数
函数 $f$ 称为是 $C^ k$ 微分流形上点 $p$ 处的 $C^ r$ 函数 $(r \leqslant k)$ ，如果在 $p$ 的某个坐标卡 $(U,\varphi)$ ， $f \circ \varphi^ {-1}$ 在 $\varphi(p)$ 是 $C^ r$ 的。

因 $\varphi \circ \tilde{\varphi} ^{-1}$ 是 $C^ k$ 的，所以若想得到坐标卡不依赖的定义，我们要求 $r \leqslant k$ 。

$C^r$ 类函数
微分流形 $X$ 上的函数 $f : X \rightarrow \mathbb{R}$ 称为是 $C^ r$ 的，如果它在 $X$ 上的每一点都是 $C ^r$ 的。微分流形 $X$ 上的所有 $C ^r$ 函数的集合，记为 $\mathscr{F}^ r (X)$ 。

可微映射

流形间的映射

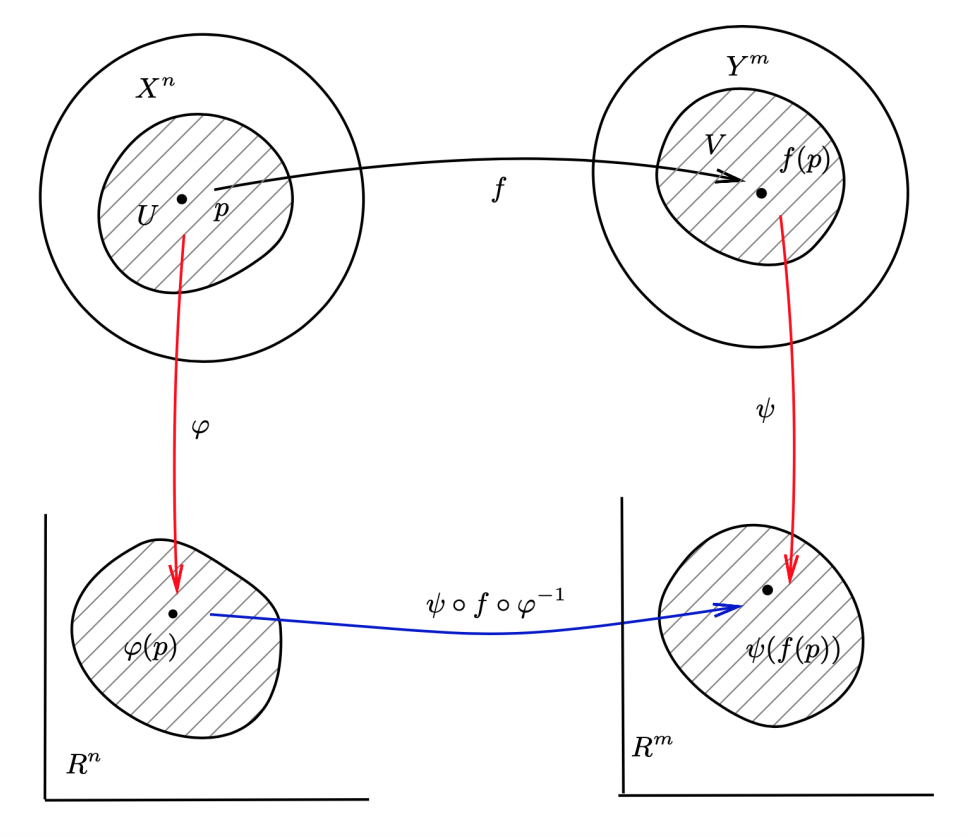
设 $X^n$ 和 $Y^m$ 是两个 $C^k$ 微分流形， $f$ 是一个映射： $f : X^n \rightarrow Y^m$ 。设 $(U,\varphi)$ 是 $X_ n$ 的一个坐标卡，而 $(V,\psi)$ 是 $Y_n$ 的一个坐标卡，则映射 $\mathcal{F}$ ：

$\mathcal{F} = \psi \circ f \circ \varphi ^{-1}$

这是一个由 $\mathbb{R}^n$ 中的开集到 $\mathbb{R}^m$ 中开集的映射。

流形间的映射 $f$ 称为在点 $p\in X^n$ 称为是 $C^r$ 可微的 ( $r\leqslant k$ )，若映射 $\mathcal{F} = \psi \circ f \circ \varphi ^{-1}$ 在 $\varphi(p)$ 是 $C^r$ 可微的，即：

$y^I = \mathcal{F}^I(x^1,\cdots,x^n),\quad I=1,\cdots,m$

是 $m$ 个 $C^r$ 个可微函数，其中 $\{x^i,i=1,\cdots,n\}$ 是点 $p$ 的坐标，而 $y^I,I=1,\cdots,m$ 是点 $f(p)$ 的坐标。

其中条件 $r\leqslant k$ 保证这个可微的定义不依赖于坐标卡的选择。

若映射 $f:X^n\rightarrow Y^m$ 在点 $X^n$ 的每一点都是 $C^r$ 可微的，则称 $f$ 是 $X^n$ 到 $Y^m$ 的 $C^r$ 可微映射。

一些例子：

若取 $Y^m$ 为 $\mathbb{R}$ ，得到了我们前面有关可微函数的定义。
若取 $X^n$ 为 $\mathbb{R}$ 中的一个区间 $I$ ，则我们得到了 $Y^m$ 上的 $C^r$ 类参数曲线。

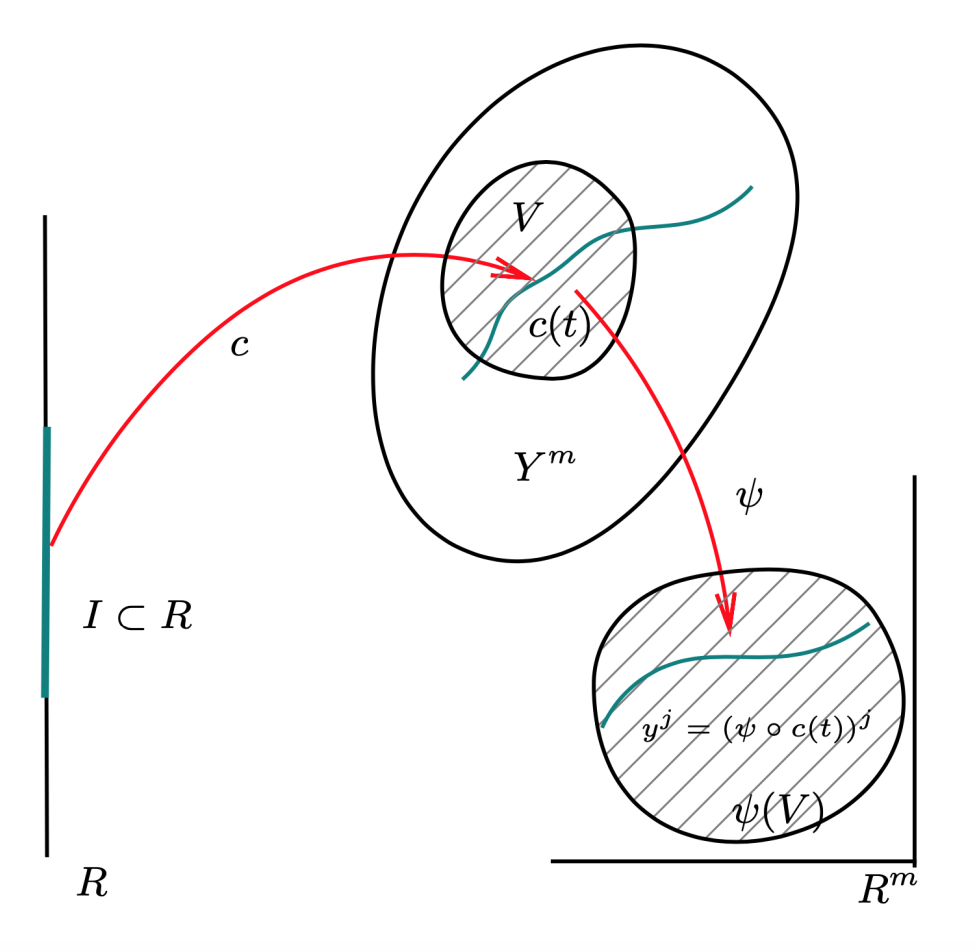
曲线
设 $X$ 是一个 $n$ -维微分流形，映射 $c : I \rightarrow X , t \mapsto c(t)$ 称为 $X$ 的一条曲线。在 $X$ 的坐标卡 $(U,\varphi)$ 下，该曲线可表示为：

$x ^ i = (\varphi \ \circ\ c(t))^ i ,\quad i = 1,\cdots ,n$

其中 $x^i$ 是这个坐标卡下的坐标。在不引起歧义时，我们也将上面的表达式简写为：

$x^i = c^i(t) \ or\ x^i = x^i(t)$

微分同胚 (diffeomorphism)
设 $X^n$ 和 $Y^n$ 是 $C^k$ 微分流形。若存在一个映射 $f : X \rightarrow Y$ 满足：

$f$ 是双射
$f$ 和 $f^{-1}$ 都是 $C^ r$ 可微的

则称 $X^n$ 和 $Y^n$ 互为 $C^r$ 微分同胚。映射 $f$ 称为是一个 $C^ r$ 微分同胚映射，或简称 $C^ r$ 微分同胚。

若两个微分结构是微分同胚的，则它们具有相同的微分结构（ $C^r$ 微分结构）。但是需要指出，两个同胚的流形不一定是微分同胚的（可能微分结构不一样）。

现在，若无特殊说明，我们假定考虑的微分流形都是光滑的，即 $k$ 足够大。所有光滑流形（对象），以及它们之间的光滑映射（态射）形成一个范畴。微分同胚对应于同构态射。

光滑函数的线性空间
光滑流形 $X$ 上的所有光滑函数的集合 $\mathscr{F}^\infty (X)$ 形成一个 $\mathbb{R}$ 上的线性空间，可以简记为 $\mathscr{F}(X)$ 。加法和数乘定义为

$\begin{aligned} &(f_ 1 + f_ 2 )(p) = f_ 1 (p) + f_ 2 (p), (λf)(p) = λf(p)\\ &\qquad \forall f_1 ,f_ 2 \in \mathscr{F}(X),\ \forall p \in X ,\ \forall \lambda \in \mathbb{R}\\ \end{aligned}$

光滑函数环
事实上，我们还可以在这个线性空间 $\mathscr{F}(X)$ 中定义一个乘法：

$(f_ 1 f_ 2 )(p) = f_ 1 (p)f_ 2 (p)$

使得 $\mathscr{F}(X)$ 在这样的加法和乘法下成为一个环。当然它也是实数域 $\mathbb{R}$ 上的一个代数。

光滑函数的拖回映射 (pull back)
在微分几何中，拖回是将一个流形上某种结构转移到另一个流形上的一种方法。
设 $\Phi : X \rightarrow Y$ 是一个光滑映射。则映射 $\Phi$ 诱导出 $\mathscr{F}(Y )$ 到 $\mathscr{F}(X)$ 的映射 $\Phi^*$ 。若 $g \in \mathscr{F}(Y )$ ， $\Phi^* g$ 定义为 (映射的复合)：