近自由电子近似、平面波法、紧束缚近似等都可以计算能带,不同的方法解决不同的问题。思路都是使用 Bloch 函数族对波函数进行展开。
紧束缚近似(TBA)
Wannier 函数
紧束缚近似(Tighting-binding approximation) 是将布洛赫波用一组正交、完备的局域函数基展开得到。
考虑到布洛赫函数具有以下性质:
ψkn(r)=ψk+Kh,n(r)(1)
其是一个倒格矢的周期函数,可以使用正格矢进行展开:
ψkn(r)=N1Rm∑an(Rm,r)eik⋅Rm(2)
其中 an(Rm,r) 就称为 Wannier 函数。
an(Rm,r)=N1k∑e−ik⋅Rmψkn(r)=N1k∑eik⋅(r−Rm)ukn(r−Rm)(3)
Wannier 函数是以宗量 r−Rm 的函数,说明它是以格点 Rm 为中心的局域波函数。可以记为:
an(Rm,r)=an(r−Rm)(4)
利用布洛赫函数的正交完备性,可以证明 Wannier 函数确实构成一个正交完备基。
- 不同能带、不同格点的 Wannier 函数严格正交:
∫an∗(r−Rm)an′(r−Rm′)dr=N1k∑k′∑ei(k⋅Rm−k′⋅Rm′)∫ψkn(r)∗ψk′n′(r)dr=N1k∑k′∑ei(k⋅Rm−k′⋅Rm′)δnn′δkk′=δmm′δnn′(5)
- 不同能带、不同格点的 Wannier 函数组成一个完备基:
n∑l∑an∗(r−Rl)an(r′−Rl)=N1n∑l∑k∑k′∑ei(k−k′)⋅Rlψkn∗(r)ψk′n(r′)=n∑k∑k′∑ψkn∗(r)ψk′n(r′)δkk′=n∑k∑ψkn∗(r)ψkn(r′)=δ(r−r′)(6)
最后一步应用了布洛赫函数的正交完备性。
紧束缚近似
前面我们得到了周期势场中单电子波函数可以用一组正交、完备的定域波函数展开:
ψkn(x)=N1Rm∑eik⋅Rman(r−Rm)(7)
至此的讨论都是严格的。现在问题的关键在于选取一组怎样的 Wannier 函数。作为一种近似,假定晶体中每个原子都对电子有较强的束缚,电子的行为十分接近于孤立原子中的电子。由此,我们可以近似使用孤立原子的定域波函数 φi(r−Rl) 作为 Wannier 函数。
φi(r−Rm) 作为孤立原子的波函数,满足如下波动方程:
[−2mℏ2∇2+V(r−Rm)]φn(r−Rm)=Enφn(r−Rm)
其中 V(r−Rm) 就是孤立原子的势,指标 n=s,p,d,f,⋯,相当于原子的不同轨道。
如此,(7) 式可以写为:
ψkn(x)=N1Rm∑eik⋅Rmφn(r−Rm)
在紧束缚近似下,可以认为不同原子对应的局域波函数的交叠程度很小,因此有如下关系近似成立:
∫φn∗(r−Rm)φn(r−Rm′)dr∼δmm′(8)
代入周期势场单电子薛定谔方程中,得到:
[−2mℏ2∇2+U(r)−E](N1Rm∑eik⋅Rmφn(r−Rm))=0(9)
利用 (8),可以将 (9) 写为:
Rm∑N1eik⋅Rm[(En−E)+U(r)−V(r−Rm)]φn(r−Rm)=0(10)
左乘 φn∗(r−Rm′),并对 dr 积分:
N1eik⋅Rm′(En−E)+Rm∑N1eik⋅Rm∫φn∗(r−Rm′)(U(r)−V(r−Rm))φn(r−Rm)dr=0
令 ξ=r−Rm:
可以将上式左边第二项的积分写为:
∫φn∗(ξ−(Rm′−Rm))(U(ξ)−V(ξ))φn(ξ)dξ=−J(Rm′−Rm)(11)
进一步得到:
N1eik⋅Rm′(En−E)−Rm∑N1J(Rm′−Rm)eik⋅Rm=0
可得:
E−En=−Rm∑J(Rm′−Rm)eik⋅(Rm−Rm′)=−Rs∑J(Rs)e−ik⋅Rs,Rs≡Rm′−Rm
由此,可以得到采用紧束缚近似给出的电子能谱为:
E(k)=En−Rs∑J(Rs)e−ik⋅Rs(12)
考虑 k∈1BZ,将取 N 个准连续值,一个孤立原子的能级分裂为 N 个准连续的能级,形成能带。
周期势场单电子波函数是一个调幅平面波:
ψkn=N1eik⋅rukn(r)(13)
可以得到能量是倒格子上的周期函数:
En(k)=En(k+Kh)(14)
且有
En(k)=En(−k)(15)
En(k) 是 k 的多值函数。
在紧束缚近似下,各格位上孤立原子的波函数之间交叠很少,求和式中只涉及到最近邻项。当 Rs=0 时:
J0=−∫φn∗(ξ)(U(ξ)−V(ξ))φn(ξ)dξ(16)
这称为 晶场劈裂
其余的 Rs=0 对应的项称为 交叠积分
例:简单立方晶体原子中的 s 电子 φS(x) 形成的能带。
ES(k)=ESat−J0−J1Rs∑′eik⋅Rs
考虑最近邻:
Rs=±ai,±aj,±ak
得到:
ES(k)=ESat−J0−J1(eikxa+e−ikxa+eikya+e−ikya+eikza+e−ikza)=ESat−J0−2J1(coskxa+coskya+coskza)
现在对于一些特殊点进行讨论:
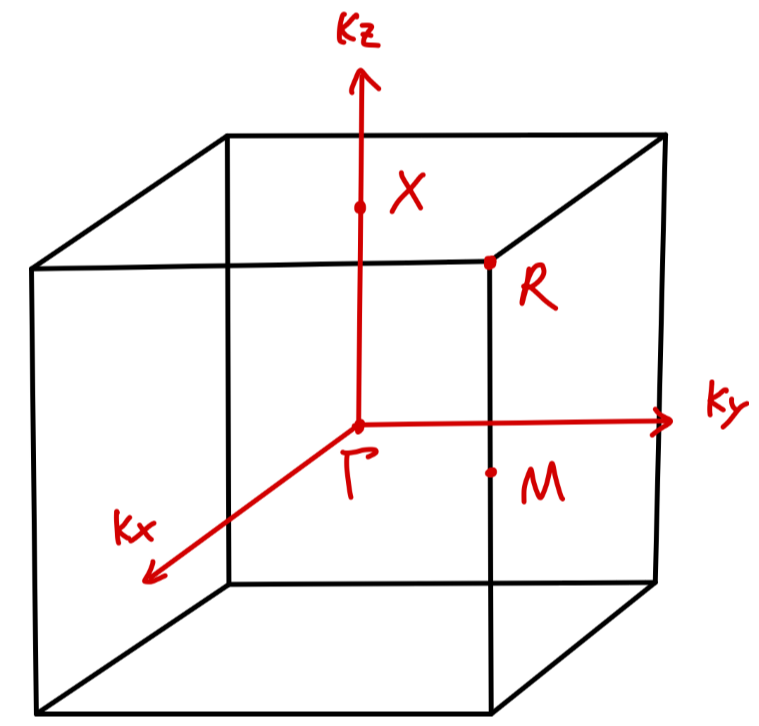
- Γ:k=(0,0,0)
EΓ=ES−J0−6J1
- R:k=(aπ,aπ,aπ)
ER=ES−J0+6J1
- X:k=(0,0,aπ)
EX=ES−J0−2J1
- M:k=(aπ,aπ,0)
EM=ES−J0+2J1
除了这四个特殊点外,再分别考虑 Γ 点附近与 R 点附近。
E(k)=ES−J0−2J1(3−21(kx2+ky2+kz2)a2)=Emin+2m−∗ℏ2k2
其中 带底有效质量 m−∗ 为:
m−∗=2a2J1ℏ2
- 在 R 点附近,有:(kx,ky,kz)=(aπ−δkx,aπ−δky,aπ−δkz)
E(k)=ES−J0−2J1(−3+21(δkx2+δky2+δkz2)a2)=Emax+2m+∗ℏ2δk2
其中 带顶有效质量 m+∗ 为:
m+∗=−2a2J1ℏ2<0
综上得到:能级宽度 ΔE=12J1。由此:能带的宽度与直接与交叠积分有关,原子之间波函数的交叠积分愈大,能带宽度愈宽。因此外层电子的波函数交叠较多,对应的能带较宽;而内层电子对应的能带较窄。
能态密度
固体能带中的能级分布是准连续的,我们使用 能态密度 来定义在能量 E 附近单位能量间隔中的状态数。固体中所有能带都可以在简约布里渊区中表示,且在 k 空间内状态均匀分布。有 k 空间内状态数密度为:
(2π)32V
此处考虑电子的自旋引入因子 2。
对于一个确定的能带 En(k),能态密度可表示为:
Nn(E)=(2π)32V∫Ω∗d3kδ[E−En(k)]=(2π)32V∫∣∇kEn(k)∣dSE(17)
考虑到能带的交叠,总的能态密度可写为:
N(E)=n∑Nn(E)(18)
自由电子态密度
现在针对自由电子求能态密度。
从自由电子能谱出发:
E=2mℏ2k2
得到:
∣∇kE∣=mℏ2k
综合得到自由电子的能态密度为:
N(E)=(2π)32V∫∣∇kE(k)∣dSE=(2π)32Vℏ24πmk=2π2V(ℏ22m)23E(19)
能带电子的态密度
现在以三维简单立方晶体紧束缚近似为例计算 s 电子的能态密度。
此时能量由以下式子给出:
Es(k)=Es−J0−2J1(coskxa+coskya+coskza)(20)
等能面可以由下图给出:
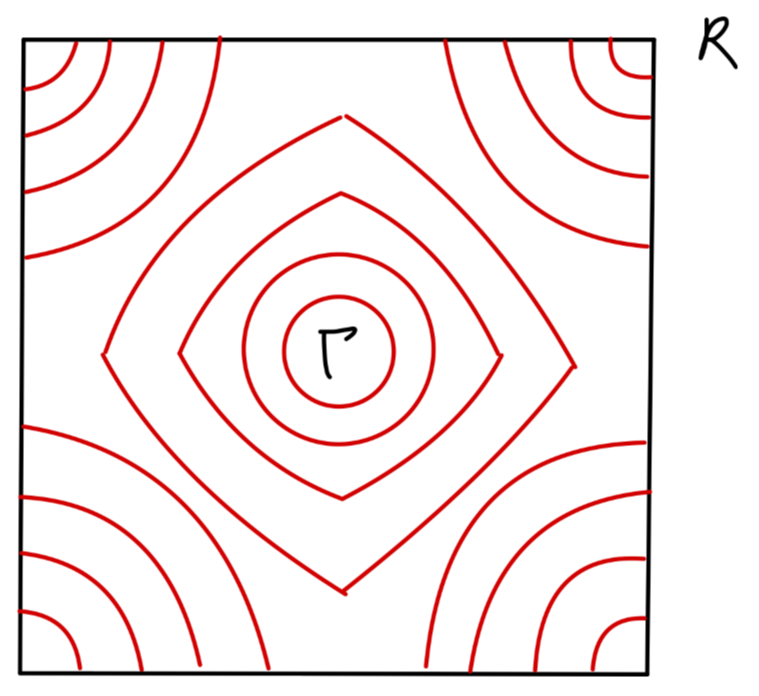
Fig:简单立方 s 带等能面
根据之前关于简单立方晶体原子中的 s 电子 φS(x) 形成的能带的讨论,可以推测在带顶和带底,能带电子的态密度同自由电子的态密度在形式上应当是一致的。
一般情况下,有:
∣∇kE(k)∣=2aJ1sin2kxa+sin2kya+sin2kza(21)
得到能态密度为:
N(E)=(2π)3aJ1V∫sin2kxa+sin2kya+sin2kzadSE(22)
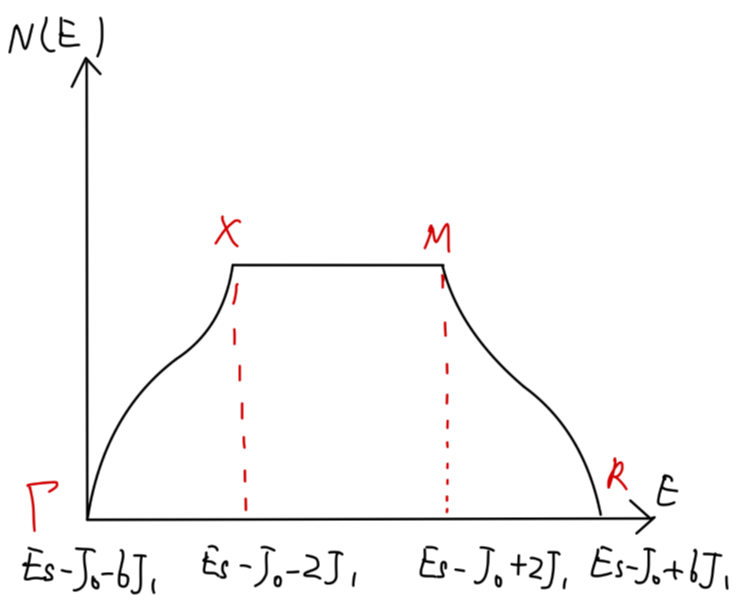
Fig:简单立方 s 电子的态密度
Γ,R 对应 ∇kE(k) 的点,另外在 X,M 点处,态密度的一阶导数也不连续。这些点被称为 范霍夫奇点。
参考资料
- 胡安 章维益 固体物理学
- 封面图 https://www.quickquantum.co.uk/tight-binding-model/













