在上篇介绍完拉格朗日方程之后,我们希望用拉格朗日力学的方法对经典力学中的问题做一些讨论。我们将分三篇分别处理有心力、微振动、刚体运动相关问题。本篇介绍有心力。有心力是很常见的,大多数两体的相互作用力是沿着两点连线方向的,这种相互作用就是有心力。常见的有心力有万有引力、库仑力、胡克力等。本篇在介绍完有心力的一般理论后,将考虑开普勒问题。
有心力的一般理论
有心力,从字面意思上理解,就是作用力始终指向力心的力。
F=Fr^
若一个质点只受到有心力作用,那么该质点的角动量守恒:
dtdL=r×F=Fr×r^=0
若有心力是保守的,那么存在势能 V,使得:
F=−∇V=−(r^∂r∂+θ^r1∂θ∂+φ^rsinθ1∂φ∂)V(r,θ,φ)
由有心力的性质可得,V 不依赖于 θ,φ;即该势能为 有心势,综合得到:
V=V(r);F=F(r)r^=−∂r∂V(r)r^
反之,若有心力 F 仅仅依赖于 r 的大小,那么构造出一个有心势是容易的,F 当然是保守的。
我们发现 F 不仅方向为径向,而且大小仅仅依赖于到力心的距离。同时,还有一些有心力大小依赖于其他坐标,例如单摆中绳的张力依赖于角位移 θ。物理学中的有心力常常指的是前一种,即一个“强版本”的有心力,以下我们在提到有心力时,也默认为是“强版本”的。
有效势
考虑一个质点在有心势 V(r) 中运动,由于 角动量守恒,质点必定在一个平面内运动。我们在这个平面内取极坐标,写出质点的拉格朗日量:
L=21m(r˙2+r2θ˙2)−V(r)
由于拉格朗日量不显含 θ,可得:
l=∂θ˙∂L=mr2θ˙=const
其中 l 为角动量,上式即为角动量守恒。我们利用 l 对拉格朗日函数做代换:
L=21mr˙2+2mr2l2−V(r)
而哈密顿量(能量)为:
H=21mr˙2+2mr2l2+V(r)
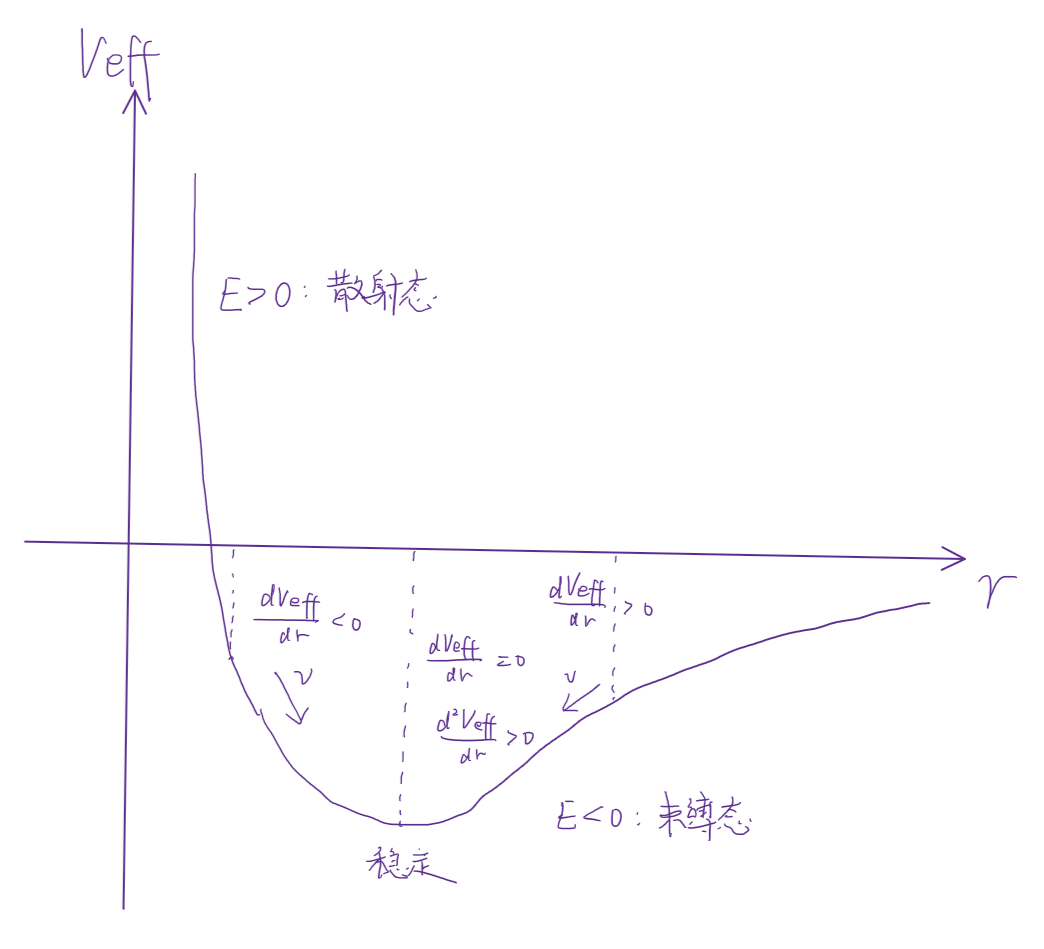
考虑到后面两项仅仅依赖于 r,我们将其总称为 有效势:
Veff=V(r)+2mr2l2
可以得到质点径向运动方程为:
mr¨=−drdVeff(r)
质点的径向运动模式是由有效势决定的。若 r→∞ 时,V(r)→0,根据有效势的大小可判断运动状态:
- Veff<0:束缚态
- Veff>0:散射态
根据有效势的一阶导数可判断径向运动的方向:
- drdVeff>0:半径减小
- drdVeff<0:半径增加
根据有效势的二阶导数可判断轨道的稳定性:
- dr2d2Veff>0:稳定
- dr2d2Veff<0:不稳定
比内公式
对于有心运动,一般的 ρ(t) 可以由下式给出:
t−t0=2m∫ρ0ρE−Veffdρ
考虑到角动量守恒,即可得 h=ρ2φ˙ 守恒,于是可以求得 φ(t):
φ(t)−φ(t0)=∫t0tρ(t)2hdt
如果我们只关心运动的轨道,有更简单的方法求解:
有心运动拉格朗日量为:
L=21m(ρ˙2+ρ2h2)−V(ρ)=21m((dtdφdφdρ)2+ρ2h2)−V(ρ)=21m(φ˙2(dφdρ)2+ρ2h2)−V(ρ)=21m(ρ4h2(dφdρ)2+ρ2h2)−V(ρ)
作代换 u=r1:
L=21mh2((dφdu)2+u2)−V(u−1)
体系能量为:
E=21mh2((dφdu)2+u2)+V(u−1)(∗)
两边对 φ 求导,容易得到:
mh2u2(dφ2d2u+u)+F=0(∗)
上述(∗)两式分别将势能和力与轨道方程联系起来,被称为 比内公式。
轨道的闭合性
根据上一节刚开始的讨论,容易得到角度随时间关系的形式解:
φ=∫2mρ2E−Veffhdρ
考虑从 ρmin 运动到 ρmax,再回到 ρmin 所转动的角度:
Δφ=2∫ρminρmax2mρ2E−Veffhdρ
选取如下形式的中心势场:
V(r)=krα
我们接下来讨论如何何种幂次的中心势能使得轨道是闭合的。例如,如下图所示,F∝r21,α=2 对应的轨道是闭合的,其他两种情况的轨道不是闭合的。其在每次公转的同时发生进动。对于闭合的轨道,有:
Δφ=2qπ,q∈Q
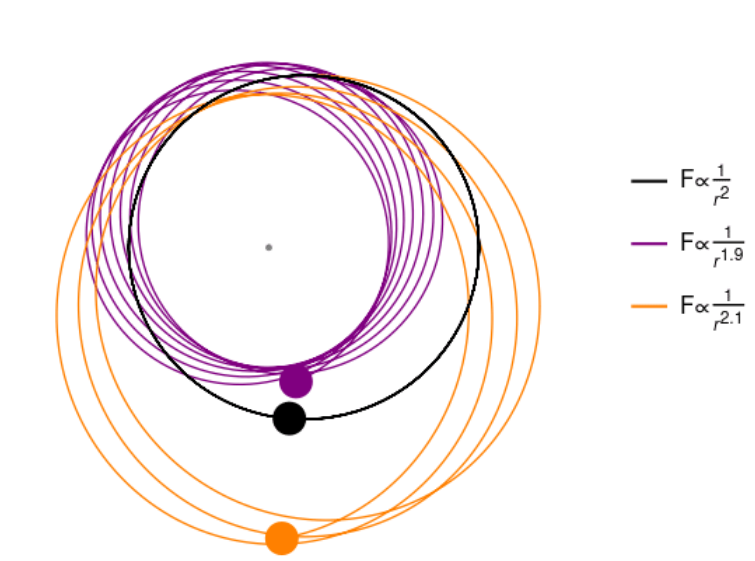
Fig:不同幂次
对应的轨道[1]
首先我们对圆轨道进行讨论,有效势能为:
Veff=krα+2r2mh2
设圆形轨道半径为 ρ0,其必定对应有效势的极值点:
Veff′(ρ0)=αkρ0α−1−ρ03mh2=0,αk>0
得到:
ρ0=(αkmh2)α+21
如果这个圆轨道是稳定的,那么要求二阶导数大于零:
Veff′′(ρ0)=α(α−1)kρ0α−2+ρ043mh2=α(α+2)kρ0α−2>0
立即得到:α>−2。
那么一般的情况呢?是否一定存在闭合的轨道呢?这个问题由 Bertrand 定理 给出:只有当 V=−kr−1(开普勒问题)或 V=kr2(胡克问题),轨道才一定闭合[2]。
接下来,我们对这个问题进行简单讨论。首先考虑对圆轨道的一个径向扰动(无穷小),封闭轨道必须要求这个圆轨道是稳定的,并且径向振动角频率与圆周运动频率满足如下关系:
qωr=φ˙,q∈Q
其中 ωr,φ˙ 分别为:
ωrφ˙=mVeff′′=mα(α+2)kρ0α−2=ρ02h
由以上三式可得到:
α=q−2−2,q∈Q
当径向扰动不可当做无穷小时,考虑轨道半径取极值的条件,此处作代换 u=r−1:
mh22E−mh22V(u)−u2=0
由此可以将一些参数用两个极值点 u1,u2 表示:
⎩⎪⎪⎨⎪⎪⎧mh22E=V2−V1u12V2−u22V1−mh22=V2−V1u2−u1
由此,可以重新改写得到从极值点 u1 到 u2,再回到 u1 的过程中转过的角度:
Δφ=2∫u1u2mh22E−mh22V−u2du=2∫u1u2(u12V2−u22V1)+(u22−u12)V(u)−u2(V2−V1)V2−V1du
那么封闭轨道就要求上述积分必须等于 2πq。考虑到 E,h,u1,u2,V1,V2 是连续变量,其连续的变化必定导致积分结果的连续性。因此,我们得到积分结果应当是与这些连续变量没有关系的。我们取一组值来计算积分,看对幂指数 α 是如何限制的。特殊的,我们选取从无穷远点开始运动的粒子,在势场作用后,又达到无穷原点的散射问题,我们作如下分类讨论:
- q−2−2>0
此时 u2=0 时 $ V_2\rightarrow\infty$,不妨取 u1=1。有:
Δφ=2∫101−u2du=−π=2qπ
可得 q=−21。此时 V=kr2。
- q−2−2<0
此时 u1=0 时 $ V_1\rightarrow 0$,不妨取 u2=1。有:
Δφ=2∫01u2−q−2−u2du=2q2π=2qπ
可得 q=1。此时 V=k/r。
开普勒问题
万有引力的引力势能具有以下形式:
U=−rk,k>0
根据我们之前所讨论的,假使质点在这种形式的势场中运动,其轨道将是完全闭合的。我们接下来对这种运动的性质做更详细的讨论。
轨道问题
由比内公式可得:
mh2u2(dφ2d2u+u)−ku2=0
容易求得:
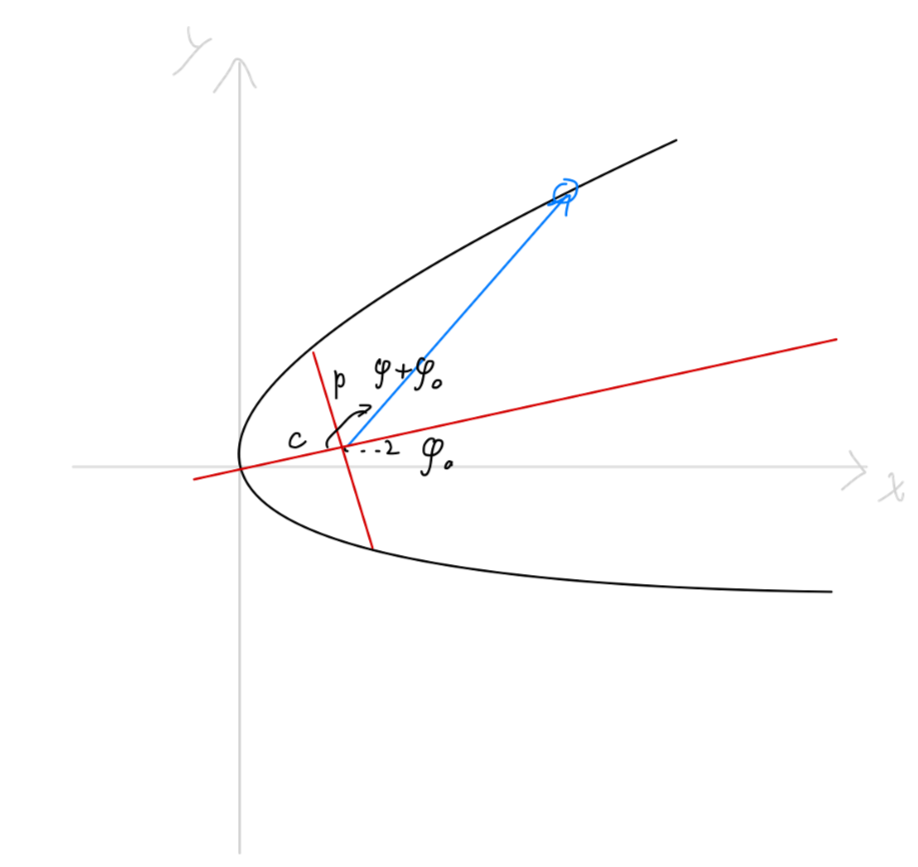
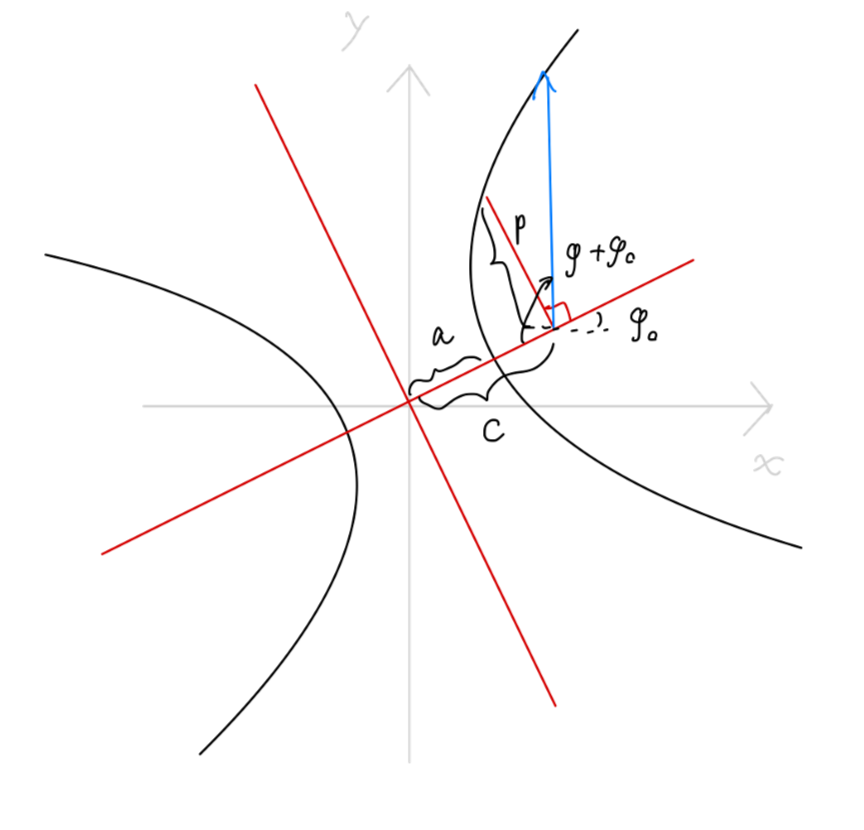
u=Acos(φ+φ0)+mh2k
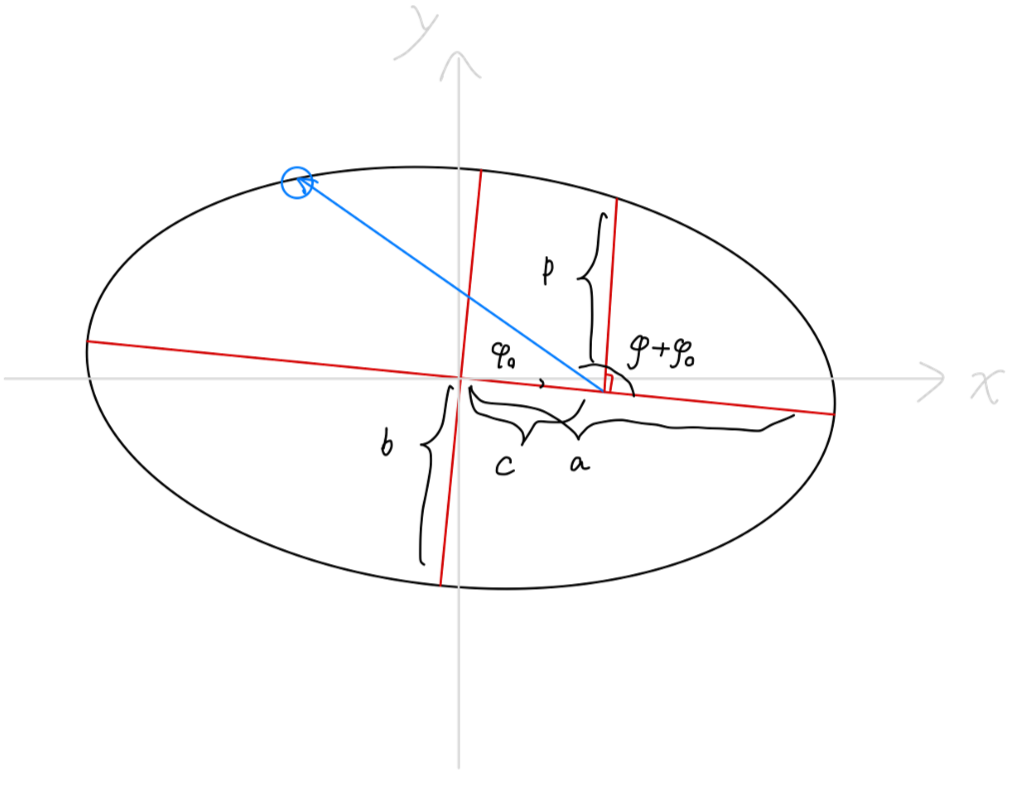
容不难看出,上式为一个圆锥曲线的极坐标方程。我们使用圆锥曲线的参量 e,p 来代入上述方程:
u=p1+ecos(φ+φ0)
或:
ρ=1+ecos(φ+φ0)p
可以得到:
p=kmh2,e=1+k22mh2E
以及圆锥曲线的半长轴与半短轴:
a=1−e2p=2∣E∣kb=1−e2p=2∣E∣mh2
做一些分类讨论:
求出椭圆面积,利用开普勒第二定律,可以很方便的求出运动周期。
运动轨道的时间依赖
对于椭圆轨道,质点运动对时间的依赖由下式积分给出:
t=2m∫E−Veffdρ=2m∫E+ρk−2ρ2mh2dρ=−2Em∫−ρ2−Ekρ+2Emh2ρdρ=∣h∣b∫−ρ2+2aρ−b2ρdρ=∣h∣b∫a2e2−(r−a)2ρdρ
自然地,我们作代换 r−a=−aecosξ[3]。容易得到,上式的积分为:
t=∣h∣b(ξ−esinξ)
对于双曲线,有类似的计算,得到:
r=a(echξ−1),t=∣h∣b(eshξ−ξ)
对于抛物线:
r=a(echξ+1),t=∣h∣b(eshξ+ξ)
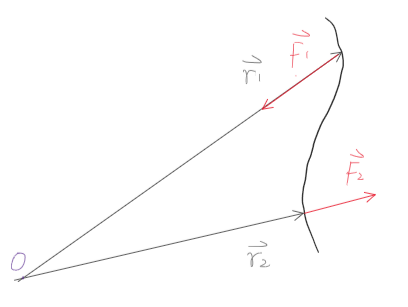
Laplace-Runge-Lenz 矢量
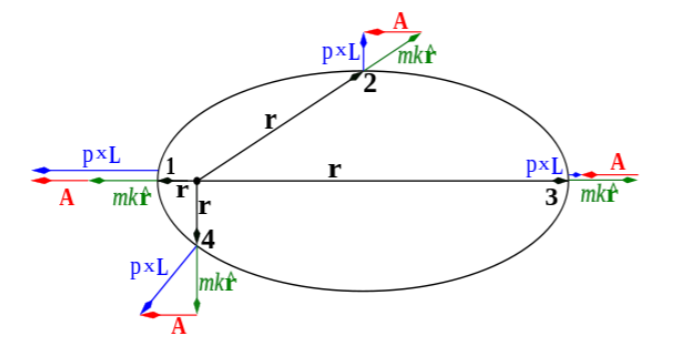
Fig:Laplace-Runge-Lenz 矢量[4]
在场 U=−rk(k 符号任意)中运动时,有一种该场所特有的运动积分。
考虑以下矢量:
A=p×L−mkr^
可得:
dtdA=dtdp×L−mkdtdr^=(−r2kr^)×L−mk(ω×r^)=(−r2kr^)×L−r2k(L×r^)=0
于是 A 成为守恒量,我们称其为 Laplace-Runge-Lenz 矢量。
我们之后将会看到,这个积分的出现与运动的简并性联系在一起 [3]。,L 和 A 这样两个守恒的矢量,对应于这个系统中存在的一种隐藏的对称性,它们可以作为 SO(4) 群的 generotor,按照 Noether 定理,正是这种对称性要求 A 是守恒的。
参考资料
- By Jacopo Bertolotti - https://twitter.com/j_bertolotti/status/1247542284616269826, CC0, https://commons.wikimedia.org/w/index.php?curid=88986624
- 王达 南京大学 理论力学讲义 7 central_force
- Landau,力学,开普勒问题
- 王达 南京大学 理论力学讲义 8 Kepler