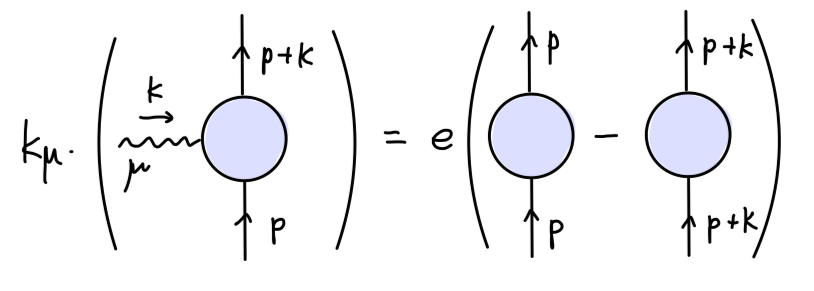Ward-Takahashi 等式
我们之前提到过 Ward 等式:若 M(k)=ϵμ(k)Mμ(k) 是某个包含一个动量为 k 的外光子的 QED 过程的跃迁矩阵元,那么若用光子动量 k 代替极化矢量 ϵ(k),将有以下等式成立:
kμMμ(k)=0(1)
现在,我们将证明 Ward 等式的推广情形:Ward-Takahashi 等式。
任意考虑一个纯 QED 的费曼图(即只存在电磁相互作用,费曼图只由QED的基本元素:如光子传播子、电子传播子,QED顶点等构成),大概长下面这个样子:
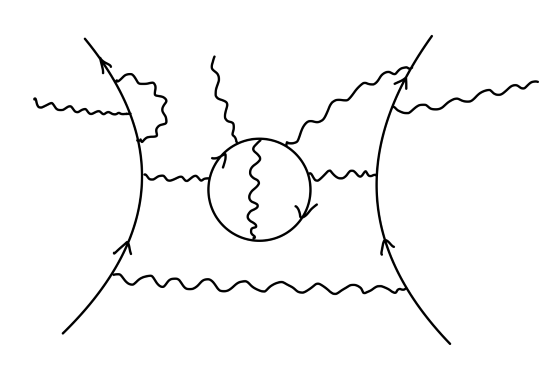
设其值为 M0。现在往上再添加一个动量为 k 的外光子,得到的费曼图为:
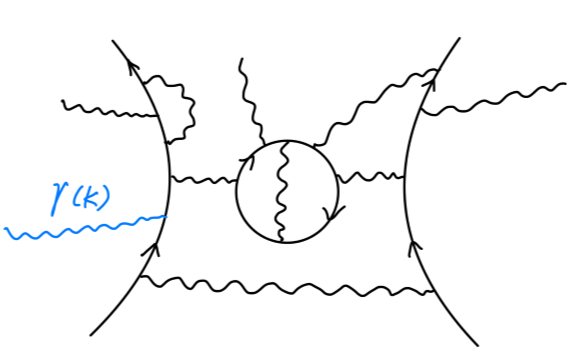
该费曼图对:M(k)=ϵμ(k)Mμ(k) 有贡献。当然,我们可以把这个外光子插入任何合理的位置上。另外通过单独考虑添加外光子后形成的顶点,通过 M0 与费曼规则,也能够得到 M(k)。以下简单说明:
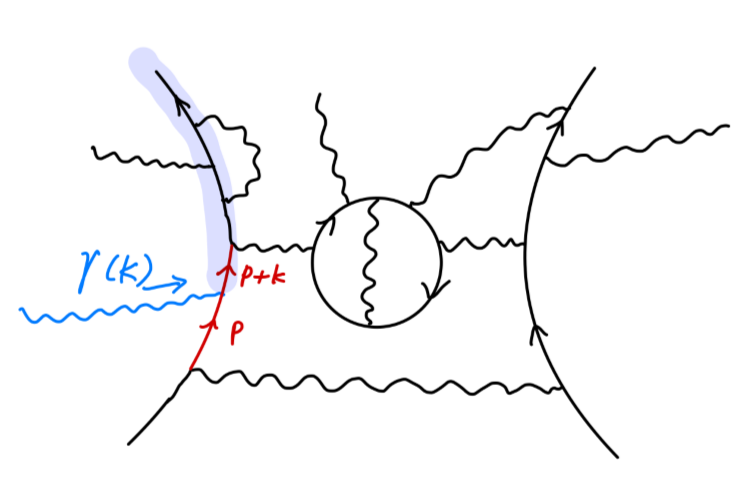
为了从 M0 得到 M(k) 只需要将原来的传播子做替换:
p−mi→kμ⋅p−mi(−ieγμ)p+k−mi=e(p−m)(p+k−m)ik=e(p−mi−p+k−mi)
最后一行将对应两个费曼图,它们均可以用 M0 表示(虽然可能依赖的动量取值不一样)。
Ward-Takahashi 的一个重要想法是:通过将所有有贡献的 M0 相加,或是将外光子插在所有可能位置的费曼图相加,都可以得到 M(k)。现在将 ϵμ(k) 替换为 kμ,以上两种思路实际上为:
insertion points∑(kμMμ(j))=e∑M0
我们现在来具体说明这件事情的含义与相关证明。
对于一般的纯 QED 图,其费米子线只存在两种情形:
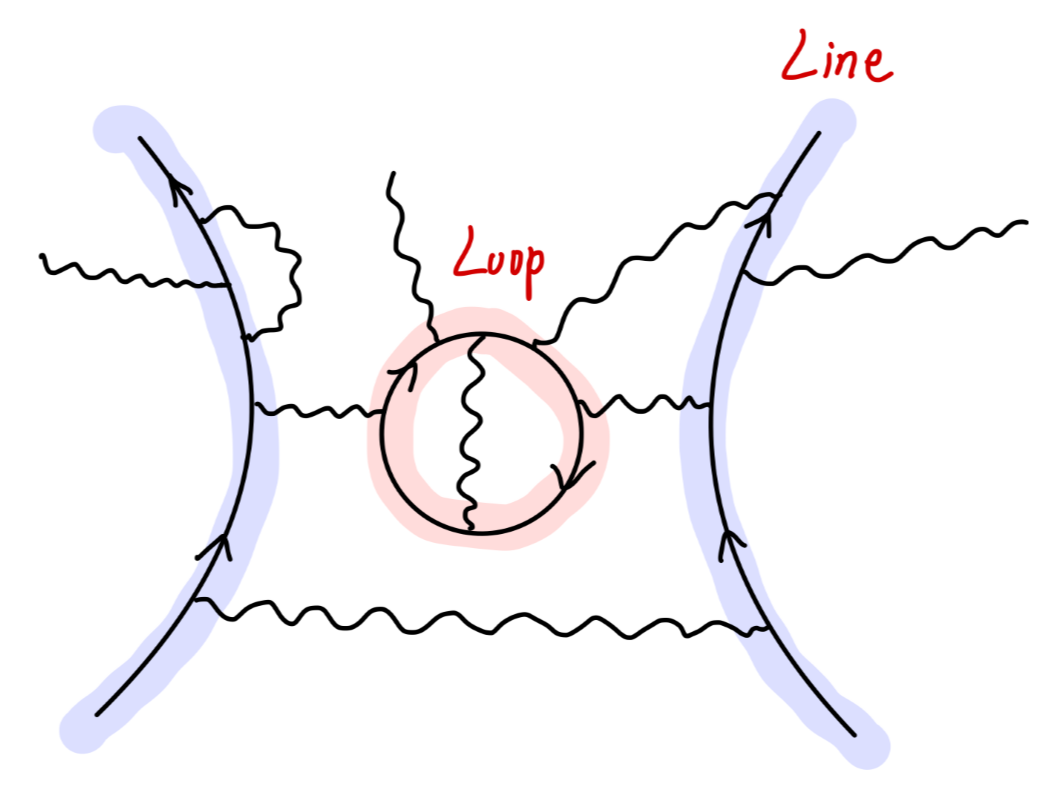
对于这两种情况,我们分别进行考虑。
对于第一种情况:
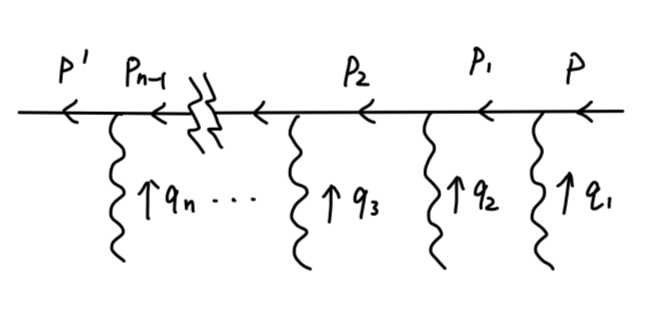
我们现在考虑在所有可能的位置,例如第 i 个光子与 i+1 个光子之间插入一个外光子。
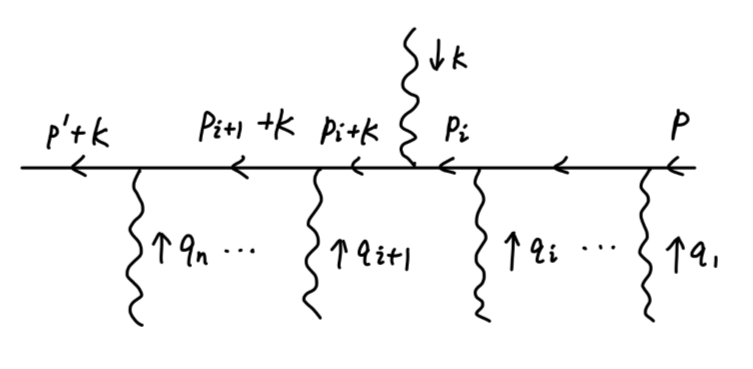
那考虑这个新的顶点对应的值为 −iγμϵμ(k),现在用 kμ 替代 ϵμ(k),那么有:
−iek=−ie[(pi+k−m)−(pi−m)]
在两边乘上对应的电子传播子得到:
pi+k−mi(−iek)pi−mi=pi+k−mi(−ie[(pi+k−m)−(pi−m)])pi−mi=e(pi−mi−pi+k−mi)
因此,在第 i 个光子和第 i+1 个光子处插入外光子后,该费曼图具有如下结构:
kμMiμ(k)=⋯(pi+1+k−mi)γλi+1(pi−mi−pi+k−mi)γλi(pi−1−mi)γλi−1⋯
同理,在第 i−1 个光子和第 i 个光子处插入外光子后,该费曼图具有如下结构:
kμMi−1μ(k)=⋯(pi+1+k−mi)γλi+1(pi+k−mi)γλi(pi−1−mi−pi−1+k−mi)γλi⋯
将以上两个式子展开后相加,注意到:其中第一个式子中的第二项将于第二个式子中的第一项相消。现在我们在所有可能的位置插入外光子,并将所得的费曼图求和,根据以上分析,以下表达式的值为(这里我们将 p′+k 重命名为 q):
i∑kμMiμ(k)=e(p−mi)⋯(q−k−mi)−e(p+k−mi)⋯(q−mi)
可以用费曼图表示为:
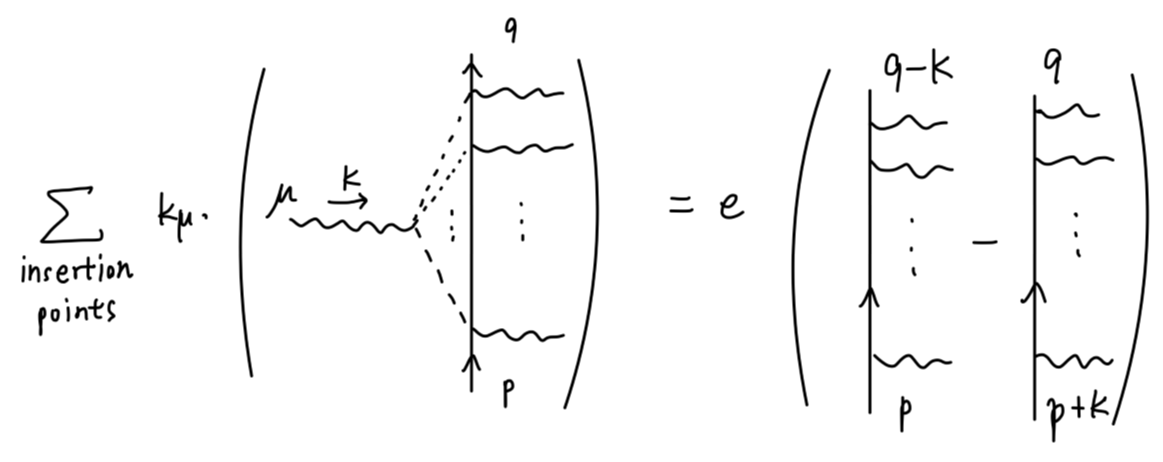
根据 LSZ 约化公式,上式左边的费曼图有一个动量为 p 的电子线进入,一个动量为 k 的电子线出去。因此其值将包含如下因子:
(p−mi)(q−mi)
而右边两个费曼图各自只含有一个如上的极点,因此我们可以下论断:右边的费曼图必定对散射矩阵无贡献。
现在考虑费米子圈的情况:
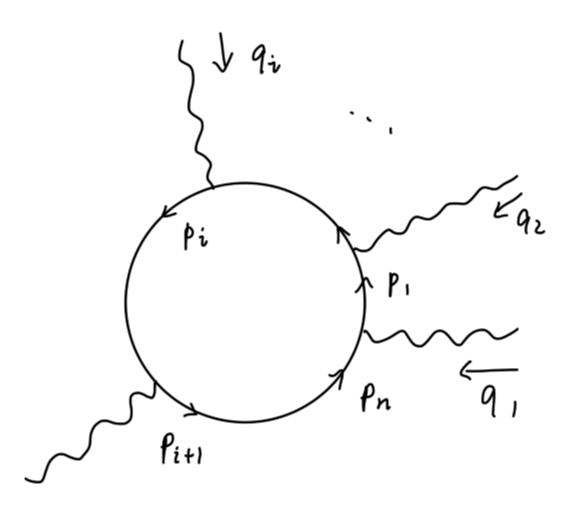
我们在中间插入一个外光子:
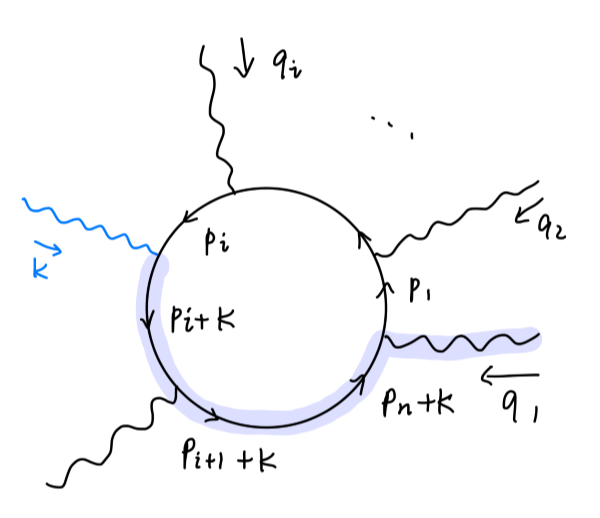
其中,我们总使动量 k 从新添加的顶点流入而从第一个顶点流出(既然是一个圈,这个流出点可以任意选取,不过我们需要使其保持一致),得到该费曼图的值为:
−e∫(2π)4d4p1tr[(pn+k−mi)γλn⋯(pi−mi−pi+k−mi)γλi⋯(p1−mi)γλ1]
我们在所有可能的位置插入外光子,并将所得的费曼图求和,得到:
−e∫(2π)4d4p1tr[(pn−mi)γλn⋯(p1−mi)γλ1−(pn+k−mi)γλn⋯(p1+k−mi)γλ1]
我们现在将以上两种情况组合起来,给出 Ward-Takahashi 等式的表述。考虑一个具有 n 个费米子线进入,n 个费米子线出去的费曼图,可以包含任意个费米子圈:
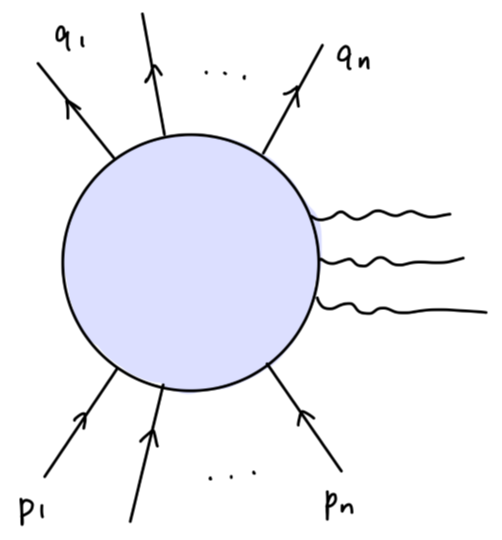
该费曼图的值设为:
M0(p1⋯pn;q1⋯qn)
现在插入一个外光子后的费曼图
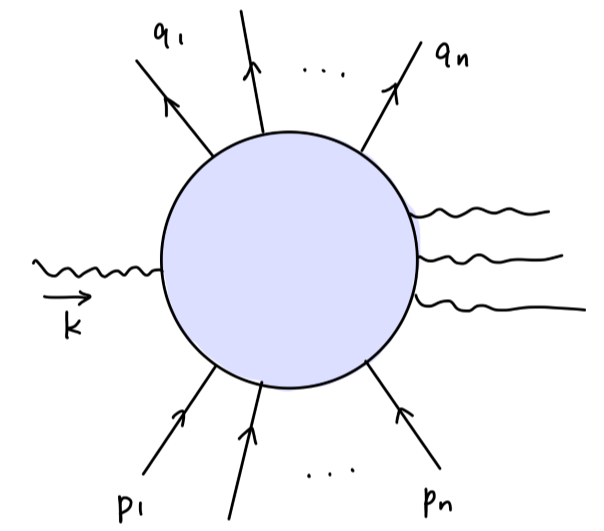
其值为:
M(k;p1⋯pn;q1⋯qn)
那么 Ward-Takahashi 等式 写为:
kμMμ(k;p1⋯pn;q1⋯qn)=ei∑[M0(p1⋯pn;q1⋯(qi−k)⋯)−M0(p1⋯(pi+k)⋯;q1⋯qn)]
用费曼图表示为:
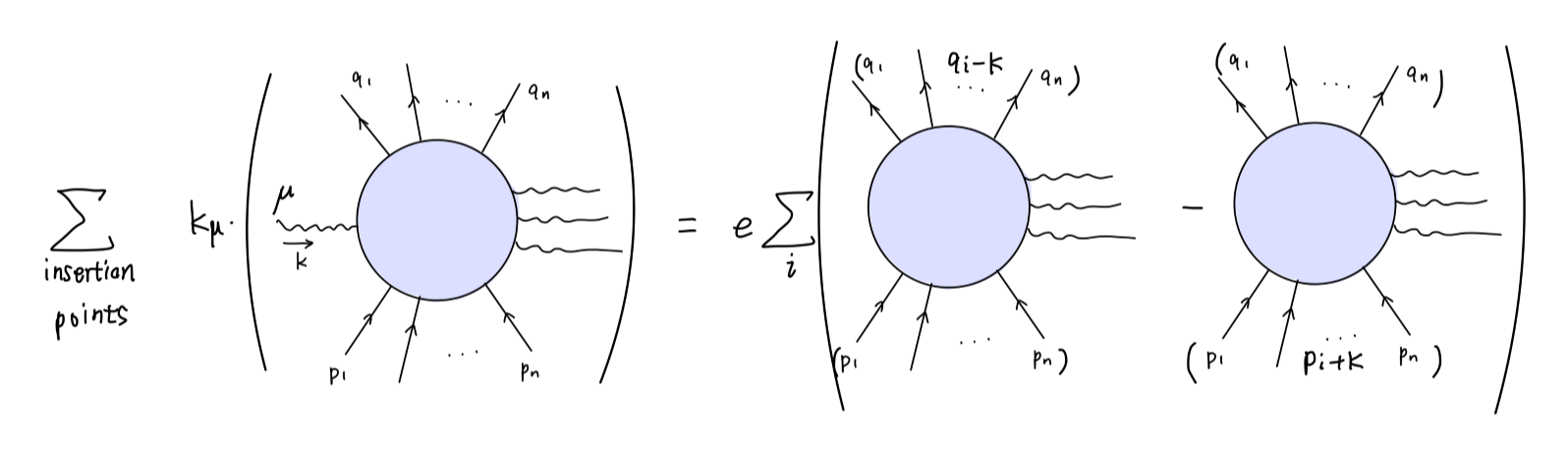
若右边对散射矩阵没有贡献,那么会有:
kμMμ=0
即得到 Ward 等式。
考虑一个最简单的例子。
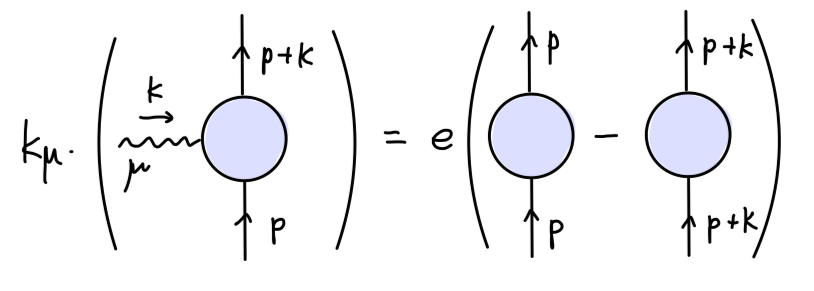
上述等式右边正对应电子传播子 S(p) 与 S(p+k),其中:
S(p)=p−m−Σ(p)i
Ward-Takahashi 等式写为:
S(p+k)(−iekμΓμ(p+k,p))S(p)=e(S(p)−S(p+k))(2)
得到:
−ikμΓμ(p+k,p)=S−1(p+k)−S−1(p)(3)
有时候,Ward-Takahashi 等式用来指以上这种特殊情形。
我们现在可以得到重整化因子 Z1 与 Z2 间的关系。在顶点修正中,我们得到:
Γμ(p+k,p)→Z1−1γμ,k→0(4)
对于电子传播子有:
S(p)∼p−miZ2
故
S−1(p+k)−S−1(p)∼−ikZ2−1,k→0(5)
结合 (4)(5) 得到
Z1=Z2(6)
即两个重整化因子 Z1,Z2 严格相等,这也是我们所讨论的某些发散能够消去的原因之一。
Ward 等式,流守恒,规范对称性具有相同的含义。Ward 等式是流守恒的图像化描述,规范对称性反映了拉格朗日量的对称性,流守恒则从运动方程角度出发。