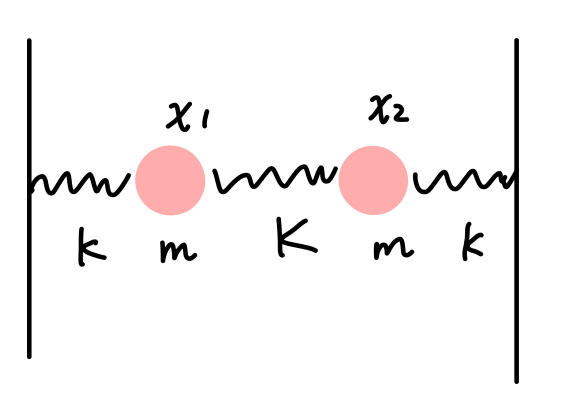理论力学笔记（七）：微振动

自由振动

在稳定平衡位置附近的运动是力学系统中一种非常普遍的运动类型，称为 微振动 $^{[1]}$ 。做振动的系统在外力的作用下物体离开平衡位置以后就能自行按其固有频率振动，而不再需要外力的作用，这种不在外力的作用下的振动称为 自由振动。理想情况下的自由振动叫无阻尼自由振动 $^{[2]}$ 。
考虑一个系统的势能 $U(q_1,q_2,\cdots,q_s)$ 。设稳定平衡位置为 $q_0=(q_{10},q_{20},\cdots,q_{s0})$ 。那么势能将在稳定平衡位置取极小值：

$\frac{\partial U}{\partial q_i}|q_{i0} = 0,\quad i=1,2,\cdots,s$

且以下矩阵是正定的：

$\bm{K} = \begin{pmatrix} \frac{\partial^2 U}{\partial q_1^2} & \frac{\partial^2 U}{\partial q_1\partial q_2} & \cdots & \frac{\partial^2 U}{\partial q_1\partial q_s}\\ \frac{\partial^2 U}{\partial q_2\partial q_1} & \frac{\partial^2 U}{\partial q_2^2} & \cdots & \frac{\partial^2 U}{\partial q_2\partial q_s}\\ \vdots & \vdots & &\vdots \\ \frac{\partial^2 U}{\partial q_s\partial q_1} & \frac{\partial^2 U}{\partial q_s\partial q_2} & \cdots & \frac{\partial^2 U}{\partial q_s^2}\\ \end{pmatrix}$

设偏移量 $x_i = q_i -q_{i0}$ ，则有：

$\begin{aligned} \delta U &= U(q_0+x) - U(q_0)\\ &= \sum_{i}\frac{\partial U}{\partial q_i}|_{q_{0}} x_i + \frac{1}{2}\sum_{ij}\frac{\partial^2 U}{\partial q_i\partial q_j}|_{q_{0}} x_ix_j +\cdots \\ &\approx \frac{1}{2}\sum_{ij}\frac{\partial^2 U}{\partial q_i\partial q_j}|_{q_{0}} x_ix_j = \frac{1}{2}\sum_{ij} K_{ij}x_ix_j\\ \end{aligned}$

注意到，在稳定平衡位置附近的势能可以被展开为一个正定的二次型。且动能天生就是一个正定二次型（动能总为正的）。其拉格朗日量可以写为：

$L = \frac{1}{2}\sum_{ij} M_{ij}\dot{x}_i\dot{x}_j -\frac{1}{2}\sum_{ij}K_{ij} x_ix_j \tag{1}$

$m_{ij}$ 为惯性系数。

现在我们试图把 $(1)$ 用矩阵形式表示，这里令：

$\bm{x} = \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_s\\ \end{pmatrix}$

$(1)$ 可以写为：

$L = \frac{1}{2}\bm{\dot{x}}^T\bm{M}\bm{\dot{x}} - \frac{1}{2}\bm{x}^T\bm{K}\bm{x} \tag{2}$

其中 $\bm{K},\bm{M}$ 为实对称矩阵。用 $(2)$ 就能够给出拉格朗日方程，完成了对该系统的求解。我们注意到若 $(1)$ 方程中自由度数大于1，这对应多自由度振动子；一般情况下，不同自由度是耦合在一起的，我们称其为 耦合振子。一个最简单的情况，当自由度只有1时，即 单振子。在自由振动情况下，通过正交变换，任何耦合振动都能够化为其自由度数目的单振子相加（解耦）。以下我们先讨论单振子问题。

单振子

在 $s=1$ 的情况下，将 $(2)$ 写为一个标量方程：

$L = \frac{1}{2}m\dot{x}^2 - \frac{1}{2}kx^2 \tag{3}$

这就是一个简单谐振子的拉格朗日量，对应的运动方程为：

$m\ddot{x} + kx =0 \tag{4}$

解为：

$x = A\sin \omega t + B\cos \omega t ,\quad \omega =\sqrt{\frac{k}{m}} \tag{5}$

或利用复指数写为：

$x = A e^{i\omega t} + B e^{-i\omega t},\quad \omega =\sqrt{\frac{k}{m}} \tag{6}$

若采用复指数的写法时方便推导的，但需要注意，其实部才对应实位移。

上述的方法是比较直观的，现在再来介绍一种思路。对于这种振动方程，试探解的方式更有效，我们直接“猜” $x(t)$ 的形式：

$x(t) = Ae^{i\omega t} \tag{7}$

代入 $(4)$ 得到：

$(-m\omega^2 + k)x(t) =0\rightarrow \omega = \sqrt{\frac{k}{m}}$

直接根据上述方程应解得 $\omega = \pm\sqrt{\frac{k}{m}}$ ，但我们舍去了负值。因为这两个解并不是独立的（单振子的自由度数为1）。

相比于时域，振动在频域中的物理形式更简单，考虑试探解 $(7)$ ，进行傅里叶变换：

$\tilde{x}(\omega) = \frac{1}{2\pi}\int Ae^{i\omega t} e^{-i\omega' t} d\omega ' = A\delta(\omega-\omega')$

对应的，我们考虑将方程 $(4)$ 进行傅里叶变换，得到：

$-m\omega^2\tilde{x} + k\tilde{x} = 0 \rightarrow \omega = \sqrt{\frac{k}{m}}$

多自由度振子

此时系统的自由度 $s>1$ ，利用多自由度振子的拉格朗日量 $(2)$ ，得到运动方程：

$\bm{M}\ddot{\bm{x}} + \bm{K}\bm{x} = 0 \tag{8}$

注意到单振子问题的解为一个频率为 $\omega$ 的振动模式；对于多自由度来说，其解为 $s$ 个振动模式的线性叠加。对于每个频率为 $\omega$ 的振动模式，有：

$\dot{\bm{x}} = i\omega \bm{x},\quad \ddot{\bm{x}} = -\omega^2 \bm{x} \tag{9}$

代入 $(8)$ 得到：

$(-\omega^2\bm{M}+\bm{K})\bm{x} =0 \tag{10}$

要求这个方程存在非零解，有：

$\det(-\omega^2\bm{M}+\bm{K})=0 \tag{11}$

得到的解 $\omega_k$ 称为 简正频率，对应的 $\bm{x}_k$ 称为 简正坐标。在得到所有的简正频率与简正坐标后，问题的完整解就是：

$\begin{aligned} &\bm{x} =\sum_{k}a_k\bm{x}_{k} e^{i\omega_kt}\\ &x_n =\sum_{k}a_kx_{kn} e^{i\omega_kt}\\ \end{aligned} \tag{12}$

现在不妨作一些讨论，增加简正频率与简正坐标的认识：

利用 (10) 可得：

$-\omega^2 \bm{x}^T\bm{Mx} +\bm{x}^T\bm{Kx} = 0\Rightarrow \omega^2 = \frac{\bm{x}^T\bm{Kx}}{\bm{x}^T\bm{Mx} }>0 \tag{13}$

这由 $\bm{X},\bm{K}$ 的正定性容易得到。

考虑两个不同的简正坐标 $\bm{x}_i,\bm{x}_j,i\neq j$ ，设对应的简正频率为 $\omega_1,\omega_2$ ，有：

$\left\{ \begin{aligned} &\bm{x}_2^T(-\omega_1^2\bm{M}+\bm{K})\bm{x}_1 =0\\ &[ (-\omega_2^2\bm{M}+\bm{K})\bm{x}_2]^T\bm{x}_1 =0\\ \end{aligned}\tag{14} \right.$

整理得到：

$\left\{ \begin{aligned} &\omega_1^2\bm{x}_2^T\bm{M}\bm{x}_1=\bm{x}_2^T\bm{K}\bm{x}_1 \\ &\omega_2^2\bm{x}_2^T\bm{M}\bm{x}_1=\bm{x}_2^T\bm{K}\bm{x}_1 \\ \end{aligned} \right.\tag{15}$

进而得到：

$(\omega_1^2-\omega_2^2)\bm{x}_2^T\bm{M}\bm{x}_1 = 0\tag{16}$

对于 $\omega_1\neq\omega_2$ 可得 $\bm{x}_2^T\bm{M}\bm{x}_1 = 0$ 。考虑若 $\bm{M}$ 是对角的，此时可以得到 $\bm{x}_2^T\bm{x}_1$ ，即不同简正频率对应的简正坐标是正交的。对于 $\omega_1 =\omega_2=\omega$ ，我们称这两个振动模式是简并的。一般的我们考虑频率为 $\omega$ ，简并度为 $n$ 的所有简正坐标 $\bm{x}_i,i=1,\cdots,n$ 。我们可得 $\bm{x}_1,\bm{x}_2,\cdots,\bm{x}_n$ 的任一线性组合都是简正坐标：

$(-\omega^2\bm{M}+\bm{K})\sum_{i}\bm{x}_i =0$

通过施密特对角化，我们总能找到 $n$ 个简正坐标 $\bm{x}'_i$ ，使得：

$\bm{x'}_i^{T}\bm{M}\bm{x'}_j = 0,\quad i\neq j$

引入对角矩阵 $\bm{\Omega}^2 = \mathrm{diag}(\omega_1^2,\omega_2^2,\cdots,\omega_s^2)$ ， $\bm{U} = (\bm{x}_1,\bm{x}_1,\cdots,\cdots,\bm{x}_s)$ 。如此，总共 $s$ 个运动方程可合写为：

$(-\bm{\Omega}^2\bm{M}+\bm{K})\bm{U} = 0 \tag{17}$

可得：

$\bm{\Omega}^2\bm{U}^{T}\bm{M}\bm{U} =\bm{U}^{T}\bm{K}\bm{U} \tag{18}$

在对简正坐标的讨论中。我们发现，总可以选择一组恰当的简正坐标使得 $\bm{x}_i^T\bm{M}\bm{x}_j = 0,i\neq j$ 。对应的，我们总可以找到矩阵 $\bm{U}$ ，使得 $\bm{U}^T \bm{M}\bm{U}$ 对角化。由 $(18)$ 可得， $\bm{U}^T \bm{M}\bm{U}$ 的对角化使得 $\bm{U}^T \bm{K}\bm{U}$ 也是对角的。由此，我们重新写下体系的拉格朗日量：

$\begin{aligned} L &= \frac{1}{2}\bm{\dot{x}}^T\bm{M}\bm{\dot{x}} - \frac{1}{2}\bm{x}^T\bm{K}\bm{x} \\ &= \frac{1}{2}\dot{\bm{x}}^T (\bm{U}^{T})^{-1} \bm{U}^{T}\bm{M}\bm{U}\bm{U}^{-1}\dot{\bm{x}}-\frac{1}{2}\bm{x}^T(\bm{U}^{T})^{-1} \bm{U}^{T}\bm{K}\bm{U}\bm{U}^{-1}\bm{x}\\ &=\frac{1}{2}\dot{\bm{y}}^T(\bm{U}^{T}\bm{M}\bm{U})\dot{\bm{y}}-\frac{1}{2}\bm{y}^T(\bm{U}^{T}\bm{K}\bm{U})\bm{y}\\ & = \sum_{i}^{s} L_i \\ \end{aligned} \tag{19}$

上式中 $\bm{y} = \bm{U}^{-1}\bm{x}$ ，代表简正模式。至此，我们把耦合的拉格朗日量使用简正坐标进行变量分离，化为了 $s$ 个独立的简正模式。

这里举一个简单的例子。考虑 k-m-K-m-k 振子，系统的拉格朗日量为：

$L = \frac{1}{2}{m}(\dot{x}_1^2+\dot{x}_2^2)-\frac{1}{2}kx_1^2-\frac{1}{2}K(x_1-x_2)^2-\frac{1}{2}kx_2^2\tag{20}$

有：

$\bm{M} = \begin{pmatrix} m & 0\\ 0 & m\\ \end{pmatrix}\quad \bm{K} = \begin{pmatrix} K+k & -K\\ -K & K+k\\ \end{pmatrix}$

本征频率为：

$\begin{aligned} &\det(\bm{K}-\omega^2\bm{M}) =(K+k-m\omega^2)^2 - K^2=0 \\ &\Longrightarrow \omega_1 = \sqrt{\frac{k}{m}},\ \omega_2 = \sqrt{\frac{2K+k}{m}} \end{aligned}$

对应的简正坐标：

$\begin{aligned} &\omega_1=\sqrt{\frac{k}{m}},&\quad \ \xi_1 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1\end{pmatrix}\\ &\omega_2=\sqrt{\frac{2K+k}{m}},&\quad \xi_2 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1\end{pmatrix}\\ \end{aligned}$

分别对应质心运动与相对运动。

分子振动

分子振动是多自由度振子中一个重要的（有趣的）例子。这里仅仅讨论一些简单的情形。

平动有 $3$ 个自由度，对于 $n$ 原子分子来说，总共有 $3n$ 个自由度。其中有 $6$ 个对应分子整体的平动与转动，剩下的 $3n-6$ 个自由度对应于振动自由度。对于线分子来说，绕着这个线的旋转并无意义，那么对应的振动自由度为 $3n-5$ $^{[1]}$ 。

这里与我们之前对刚体自由度的讨论并不矛盾，因为刚体无振动自由度、只有平动自由度。将原子结合在一起的化学键并不是完整的约束，并不能减小自由度。

考虑振动时，如果剔除整体的平动与转动，那么得到以下约束条件：

$\begin{aligned} & \sum_i m_i \bm{x}_i = 0\\ & \sum_i m_i \bm{x}_i\times \bm{r}_i = 0\\ \end{aligned}\tag{21}$

如果没有剔除整体运动，那么得到的零频率解就对应整体运动。

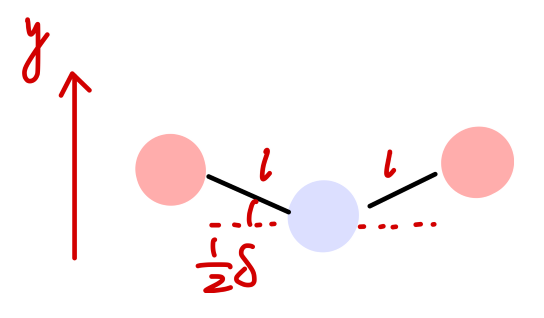
对于线性对称分子 $\mathrm{ABA}$ ，我们做一些讨论。

首先考虑纵向振动，对应的拉格朗日量为：

$L = \frac{1}{2}m(\dot{x}_1^2+\dot{x}_3^2)+\frac{1}{2}M\dot{x}_2^2-\frac{1}{2}k((x_2-x_1)^2+(x_3-x_2)^2)$

对应有：

$\bm{M} = \begin{pmatrix} m & 0 & 0\\ 0 & M & 0\\ 0 & 0 & m\\ \end{pmatrix}\quad \bm{K} = \begin{pmatrix} k & -k & 0\\ -k & 2k & -k\\ 0 & -k & k \\ \end{pmatrix}$

可以得到：

$\begin{aligned} &\omega_1 = 0,\quad &\xi_1 =\frac{1}{\sqrt{3}}\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \\ &\omega_2 =\sqrt{\frac{k}{m}},&\quad \xi_2 =\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \\ &\omega_3 =\sqrt{\frac{k(M+2m)}{Mm}},&\quad \xi_3 =\frac{1}{\sqrt{2+\frac{4m^2}{M^2}}}\begin{pmatrix} 1 \\ -\frac{2m}{M} \\ 1 \end{pmatrix} \\ \end{aligned}$

$\omega_1$ 对应整体运动， $\omega_2$ 对应对称振动， $\omega_3$ 对应反对称振动。

再考虑横向振动，此时有两个相互独立的振动方向。

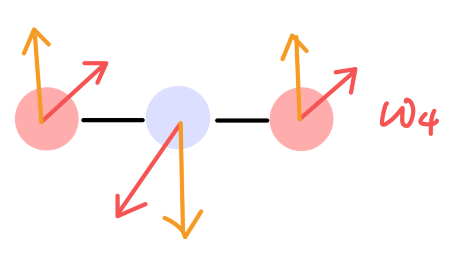
相应的振动频率与分子的弯曲势有关，这两个振动模式应当是简并的。不失一般性的，我们考虑具有如下形式的弯曲势：

$U = \frac{1}{2}k'\delta^2,\delta = \frac{y_1+y_3-2y_2}{l}$

可得分子横向振动的拉格朗日量：

$\begin{aligned} L &= \frac{1}{2}(m(\dot{y}_1^2+\dot{y}_3^2)+M\dot{y}_2^2)-\frac{1}{2}k'\delta^2\\ &=\frac{1}{2}[\frac{m}{2}(\frac{M}{2m+M})^2l^2+\frac{M}{4}(\frac{2m}{2m+M})^2l^2]\dot{\delta}^2-\frac{1}{2}k'\delta^2\\ & = \frac{1}{4}\frac{mM}{2m+M}l^2\dot{\delta}^2-\frac{1}{2}k'\delta^2\\ \end{aligned}$

得到：

$\omega_4 = \sqrt{\frac{k'(M+2m)}{Mm}}$

其简并度为2。

综上对于线性对称分子 ABA，整体的平动自由度为3，转动自由度为2，振动自由度为 4，其中2个对应于纵向振动（对称振动，反对称振动），2个对应于横向振动（简并）。

以上讨论的为自由振动。现在其他类型的微振动问题做一些简单讨论。以下均以单振子为例进行说明。

简谐振子一般讨论

简谐振子就是线性的振子，一般情况下，其动力学方程为：

$m\ddot{x} + \gamma \dot{x} + kx = f(t) \tag{22}$

$(22)$ 式中 $\gamma\dot{x}$ 为 阻尼项，运动速度越大，阻尼力越大； $f(t)$ 为外力。在自由振子情况下，这两项都为零。对于考虑阻尼项与外力的一般情况，我们首先将 $(22)$ 进行傅里叶变换：

$(-m\omega^2 + i\omega\gamma + k)\tilde{x}(\omega) = \tilde{f}(\omega) \tag{23}$

进行分类讨论，

对于 $\tilde{f}(\omega)=0$ 。有：

$(-m\omega^2 + i\omega\gamma + k)\tilde{x}(\omega) = 0$

应当有：

$-m\omega^2 + i\omega\gamma + k = 0$

解得：

$\omega_{\pm} = \frac{i\gamma\pm\sqrt{-\gamma^2+4km}}{2m} = \frac{i\gamma}{2m}\pm \sqrt{\omega_0^2 - \frac{\gamma^2}{4m^2}}$

其中 $\omega_0 =\sqrt{k/m}$ 。可以进一步分为三种情况：

$\omega_o>\frac{\gamma}{2m}$ ：欠阻尼
记 $\sqrt{\omega_0^2 - \gamma^2/(4m^2)} = \nu$
则其解为：

$x(t) = (A\sin\nu + B\cos\nu)e^{-\gamma t/(2m)}$

$\omega_o<\frac{\gamma}{2m}$ ：过阻尼
记 $\sqrt{\gamma^2/(4m^2)-\omega_0^2} = \nu$
则其解为：

$x(t) = (Ae^{\nu t} + Be^{-\nu t})e^{-\gamma t/(2m)}$

$\omega_o=\frac{\gamma}{2m}$ ：临界阻尼
则其解为：

$x(t) = (A+ Bt)e^{-\omega_0t}$

下图中，横坐标为时间，纵坐标为幅度（均为相对值）， $damping$ 参量定义为：

$damping \equiv \frac{\gamma}{2m\omega_0}$

固定 $\omega_0,m$ 改变 $\gamma$ ，下图展示了得到的解。

$damping > 1$ ：过阻尼
$damping = 1$ ：临界阻尼
$damping < 1$ ：欠阻尼

可以改变 $damping$ 参量，观察得到的阻尼振荡解。

对于 $\tilde{f}(\omega)\neq0$ 。（受迫振动）有：

$\begin{aligned} \tilde{x}(\omega) &= \frac{\tilde{f}(\omega)}{-m\omega^2 + i\omega\gamma + k}\\ &= \frac{e^{i\delta}}{\sqrt{(\omega^2-\omega_0^2)^2 + \frac{\gamma^2}{m^2}\omega^2}} \frac{\tilde{f}(\omega)}{m}\\ \end{aligned} \tag{24}$

其中 $\delta = \mathrm{Arg}(m\omega^2 -k - i\omega\gamma )$ 。当 $\gamma < \sqrt{2} m\omega_0$ 时，在 $\omega = \sqrt{\omega_0^2 - \gamma^2/2m^2}$ 处发生共振。

一个比较特殊的情况是 $\gamma = 0, \tilde{f}(\omega) = f_0\delta(\omega-\omega_0)$ ，对应 $(24)$ 式的积分失效。回到 $(22)$ 式，得到：

$k\ddot{x}+mx = f_0e^{i\omega_0 t}$

其中一个特解为：

$x(t) = \frac{f_0t}{2m\omega_0i}e^{i\omega_0t}$

此时振幅随着时间增加，微振动的条件已经不能满足，非线性效应开始体现。