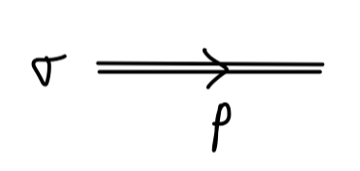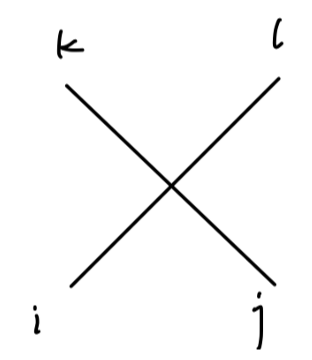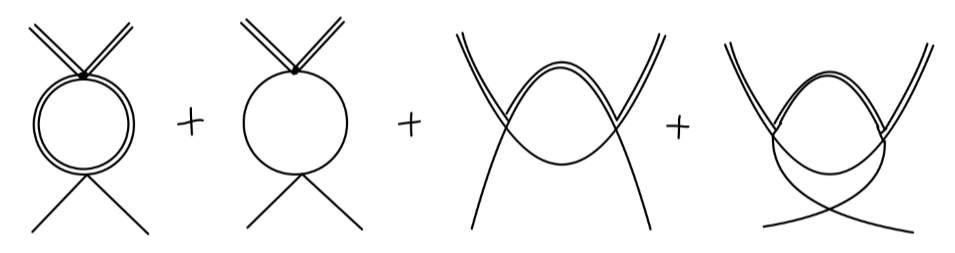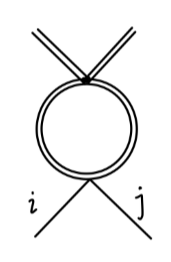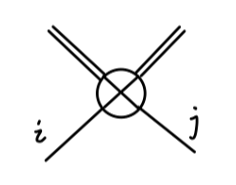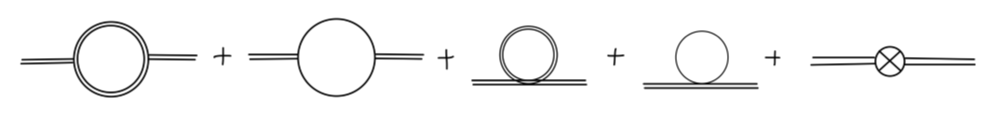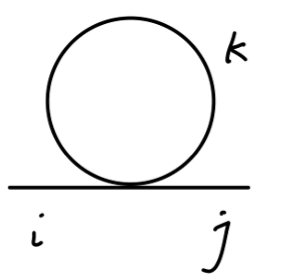对称性自发破缺
在某些情况下,系统的拉格朗日量存在某种对称性,而系统所处于的基态却并不具有这种对称性,我们称这种现象为 对称性自发破缺 spontaneously broken symmetry。对称性自发破缺是理论物理的重要概念。本篇我们尝试从一些简单的例子出发去理解这件事情。
对称性自发破缺的例子
例如对于具有以下拉氏量的系统:
L=21(∂μϕ)2+21μ2ϕ2−4!λϕ4(1)
对比 ϕ4 理论的拉氏量,是将其中的质量 m2 替换为一个负参数 −μ2
那么该体系的哈密顿量为:
H=∫d3x[21π2+21(∇ϕ)2−21μ2ϕ2+4!λϕ4](2)
其势能如下图所示:
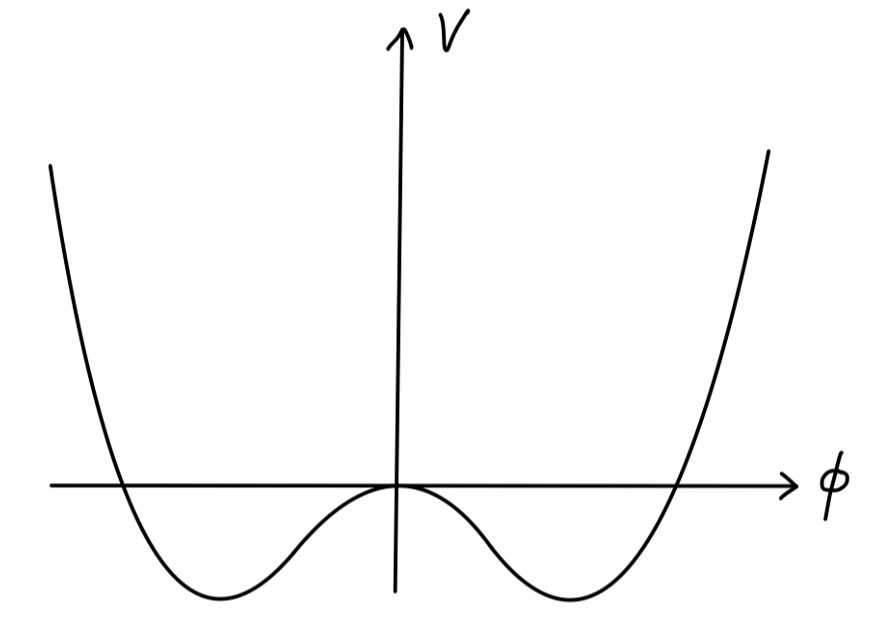
设具有能量最低的场为 ϕ(x)=ϕ0,即 ϕ0 将使得以下势能取极小值:
V(ϕ)=−21μ2ϕ2+4!λϕ4(3)
得到:
ϕ0=±v=±λ6μ(4)
现在考虑系统的能量稍微高于基态能量,不妨考虑场量在 v 附近,即有:
ϕ(x)=v+σ(x)(5)
代入 (1) 可以将拉氏量写为:
L=21(∂μσ)2−21(2μ2)σ2−6λμσ3−4!λσ4(6)
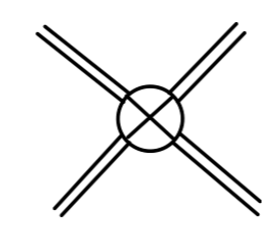
这个拉氏量描述了一个质量为 2μ 的标量场,并且带有 σ3,σ4 项的相互作用。并且我们发现原来的拉氏量带有的 ϕ↔−ϕ 的对称性不再具有了。
再以 Linear Sigma Model 为例,其的拉氏量形式为:
L=21(∂μϕi)2+21μ2(ϕi)2−4λ[(ϕi)2]2(7)
其中重复的指标 i 表示求和,即:
(ϕi)2=ϕiϕi=i=1∑Nϕi2
该拉氏量具有如下对称性:对场 ϕi 做一个旋转并不改变拉氏量:
ϕi→Rijϕj
其中 R 为一个 N×N 的正交矩阵。其将形成 N 维旋转群 O(N)。
现在考虑系统的基态 ϕ0i。其势能为:
V(ϕi)=−21μ2(ϕi)2+4λ[(ϕi)2]2(8)
能量最低的态满足:
(ϕ0i)2=λμ2(9)
我们可以任意选取 ϕ0i 的方向,不妨取 ϕ0i 为:
ϕ0i=(0,0,⋯,0,v),v=λμ(10)
现在考虑在 ϕ0i 附近的场:
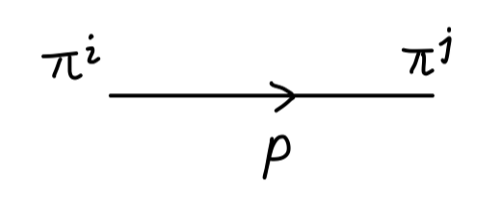
ϕi(x)=(πk(x),v+σ(x)),k=0,⋯,N−1(11)
代入拉氏量,不难得到:
L=21(∂μπk)2+21(∂μσ)2−21(2μ2)σ2−λμσ3−λμ(πk)2σ−4λσ4−2λ(πk)2σ2−4λ[(πk)2]2(12)
我们得到了一个具有质量的 σ 场和 N−1 个无质量的 π 场。对应的对称性 O(N) 被破坏了,该系统的对称性成为了 O(N−1)。
Goldstone 定理
连续对称性自发破缺导致零质量粒子的出现是一个普遍的结果,这被称为 Goldstone 定理 Goldstone’s theorem。它声称:对于任意一个自发破缺的连续对称性,都将包含一个无质量的粒子,称为 Goldstone bosons。例如 π 介子就可以被近似看作 Goldstone 玻色子。
对称性自发破缺与重整化
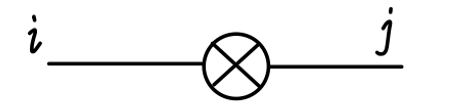
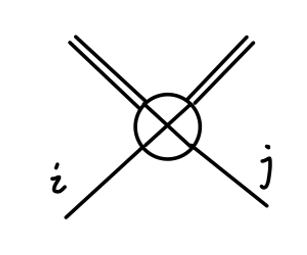
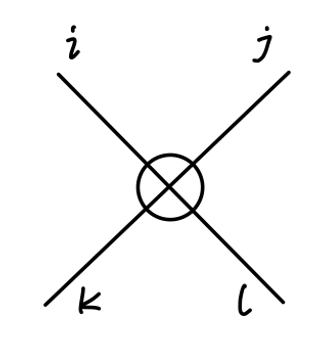
现在以 Linear Sigma Model 为例,其拉氏量可见 (12) 式,我们可以写出对应的费曼规则:
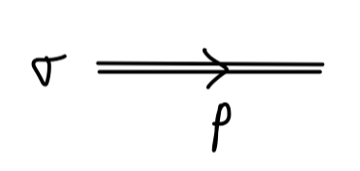
p2−2μ2i
p2iδij
−6iλv
−2iδijλv
−6iλ
−2iλδij
−2iλ[δijδkl+δikδjl+δilδjk]
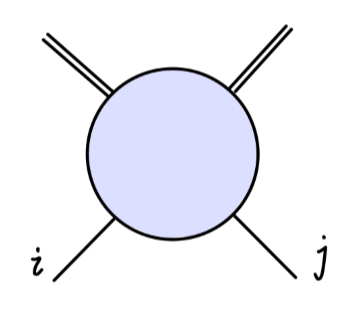
利用费曼规则,我们可以很轻松的计算 tree-level 的费曼图。对于一阶圈图来说,不幸的是,它们往往是发散的。以下我们列举出了八种表观发散的图,并且每个图可以会包含不止一个发生发散的参数。
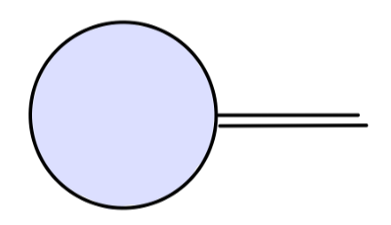
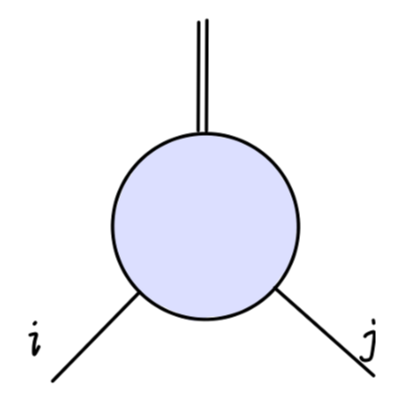
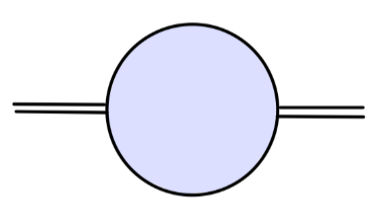

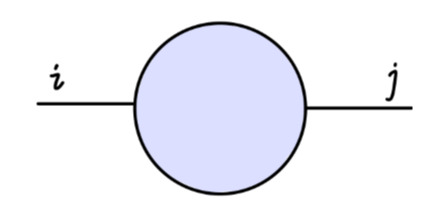
- σσππ 顶点
但问题出现了:如果我们按照之前的步骤:将原始的拉氏量写为带有 counterterms 的形式:
L=21(∂μϕi)2+21μ2(ϕi)2−4λ[(ϕ2)2]2+21δZ(∂μϕi)2−21δμ(ϕi)2−4δλ[(ϕi)2]2
写为 σ 与 π 场的形式,第二行的 counterterm 成为:
2δZ(∂μπk)2−21(δμ+δλv2)(πk)2+2δZ(∂μσ)2−21(δμ+3δλv2)σ2−(δμv+δλv3)σ−δλvσ(πk)2−δλvσ3−4δλ[(πk)2]2−2δλσ2(πk)2−4δλσ4
如此,我们得到了一系列 counterterms,但仅仅依赖于三个独立的重整化参量:δZ,δμ,δλ。我们相应的写出 counterterms 对应的费曼规则:
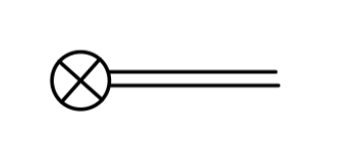
−i(δμv+δλv3)
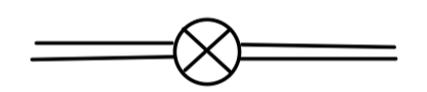
i(δZp2−δμ−3δλv2)
−6iδλ
iδij(δZp2−δμ−δλv2)
−2iδijδλ

−6iδλv
−2iδλ[δijδkl+δikδjl+δilδjk]
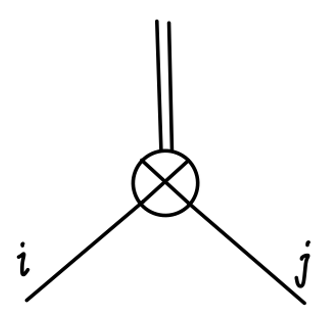
−2iδijδλv
我们能否期望通过这三个独立可调的重整化系数使上述八个图的发散消失?这件事情确实发生了!下面我们来讨论这件事。
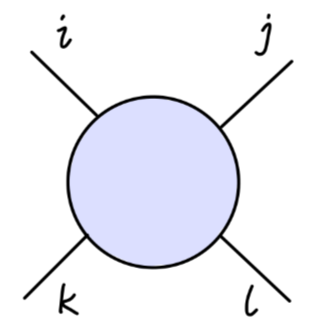
四点关联函数与三点关联函数
重整化条件
既然只含有三个可调的重整化系数,相应的,我们只需要选择三个重整化条件。类比之前对于 ϕ4 场的重整化条件,当然我们也可以选取 σ 场的质量、场强以及特定取值的散射振幅为重整化条件。不过这里,我们可以技巧性地选择将其中一个重整化条件替代为对 σ 的一点关联函数的限制:
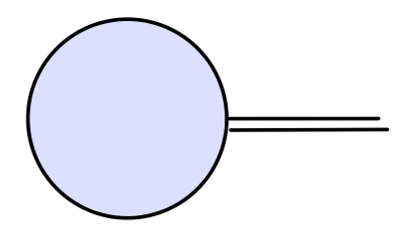
其值为
0
在 QED 中,对应的一点关联函数将会自动消除。而对于 linear sigma model,并没有对称性限制使得一点关联函数会消失。相应的一点关联函数将会产生一个 σ 场的非零期望值。
对应的重整化条件为:
其值为
0
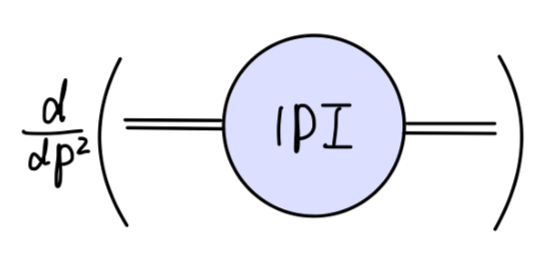
其值为
0,at p2=m2
其值为
−6iλat s=4m2, t=u=0
我们将要看到:这些重整化条件能够使得 linear sigma model 的所有的一阶圈图取有限值。
重整化条件:4σ 顶点
首先我们通过计算 4σ 图来确定 δλ。4σ 图的一般形式为:
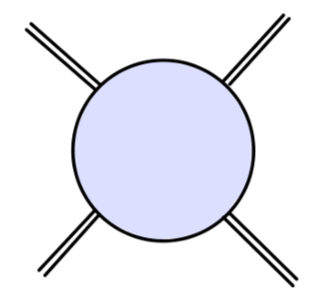
对 4σ 顶点的一阶圈图修正,包含 counterterms 为:
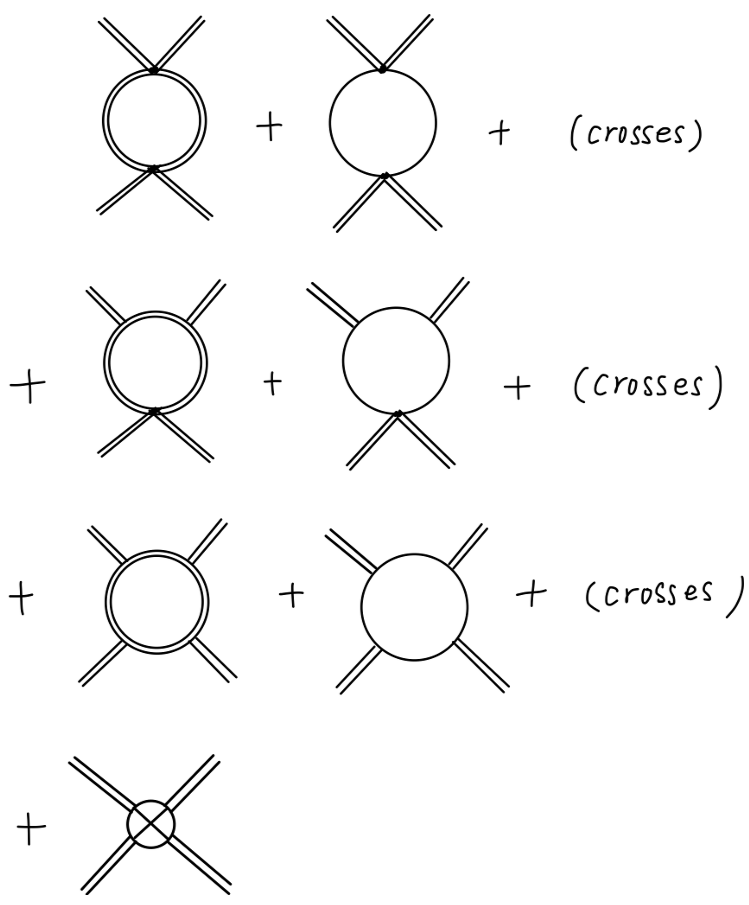
其中前三行的前两个图分别包含 σ loop 与 π loop,对应 s-channel,后面的 crosses 项包含相应的 t,u-channel 的图。最后一行为 4σ 顶点 counterterm。根据重整化条件,我们必须通过调整 δλ 来使得上述图的总和相消。因为其中有很多图的值是有限的,我们现在只关注那些紫外发散的部分,这样可以简化我们的讨论。
例如下图的值是有限的:
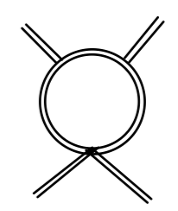
其值可估计为:
∼∫(2π)4d4kk21k21k21
在 4σ 图的一阶圈图中,所有在一个圈中包含三个及其以上传播子的图(也就是二三行)都是有限值。因此我们只需要计算第一行就能确定 δλ。
考虑如下费曼图:
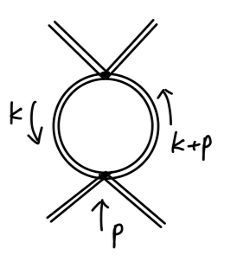
其值为:
===21⋅(−6iλ)2⋅∫(2π)dddkk2−2μ2i(k+p)2−2μ2i18λ2∫01dx∫(2π)dddk[k2−Δ]2118λ2∫01dx(4π)d/2iΓ(2−2d)(Δ1)2−2d18iλ2(4π)2Γ(2−2d)+(finite terms)
其中 Δ 是一个关于 p,μ 的函数。具体形式并不重要,因为我们现在只关注产生紫外发散的部分。
再考虑如下费曼图:
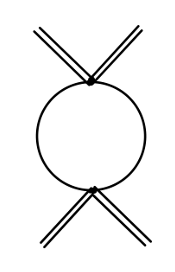
其值为:
2iλ2(N−1)(4π)2Γ(2−2d)+(finite terms)
其中 i,j 的取值为 1 到 N−1(根据 Goldstone 定理,破缺的 N−1 个自由度产生 N−1 个无质量粒子 πi),相应的缩并产生 N−1 这个因子。
不难想象:三个 channel 的费曼图的值是相等的。由此我们得到最终结果:
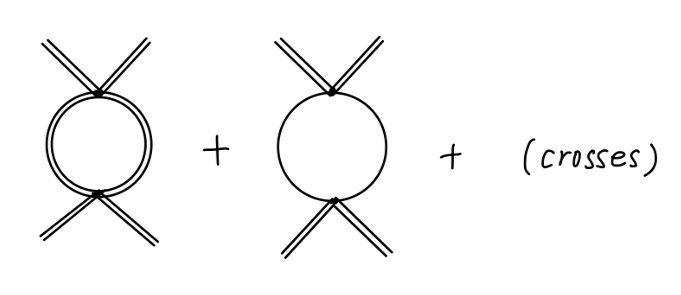
其值为:
6iλ2(N+8)(4π)2Γ(2−2d)
这样可以得到考虑一阶修正的 δλ:
δλ∼λ2(N+8)(4π)2Γ(2−2d)
现在我们使用 ∼ 来表示只进行有限修正程度下的相等。
计算完 δλ 后,我们发现其他的顶点 counterterms,例如:σσππ 顶点,3σ 顶点,4π 顶点,σππ 顶点的 counterterms 由于只含有 δλ,也会被唯一确定。现在我们想要问,是否这些关联函数也能得到有限值呢?我们现在来计算这件事。
σσππ 顶点
考虑一般的 σσππ 顶点:
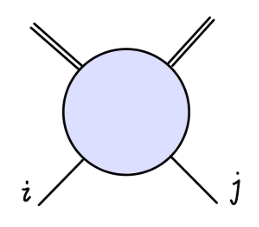
相应的一阶圈图修正为:
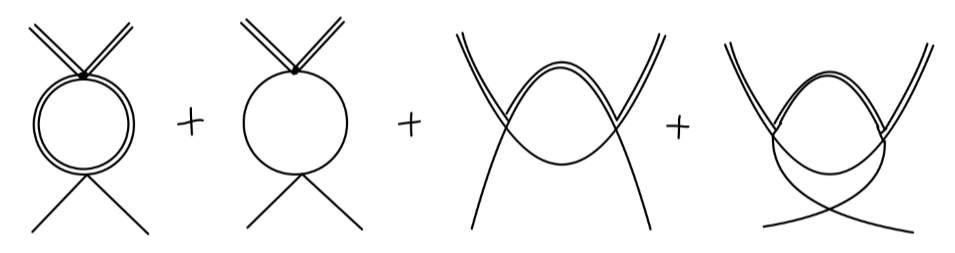
其中第一个与第二个图需要引入对称因子 21。
考虑第一个图:
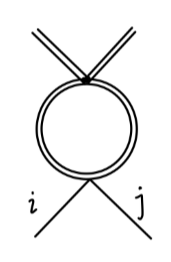
其值为:
21⋅(−6iλ)(−2iλδij)⋅(4π)2−iΓ(2−2d)=6iλ2δij(4π)2Γ(2−2d)
考虑第二个图:
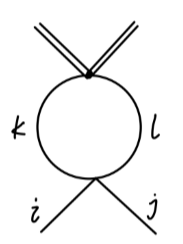
其值为:
=21⋅(−2iλδkl)⋅(−2iλ(δijδkl+δikδjl+δilδjk))⋅(4π)2−iΓ(2−2d)2iλ2(N+1)δij(4π)2Γ(2−2d)
考虑第二个图:
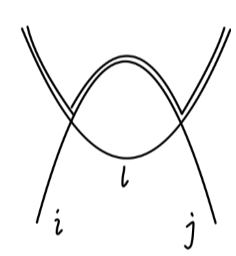
其值为:
∼(−2iλδil)(−2iλδjl)⋅(4π)2−iΓ(2−2d)=4iλ2δij(4π)2Γ(2−2d)
不难得到第四个图与上图的值相等。
将它们加起来,得到 σσππ 顶点图的值为:
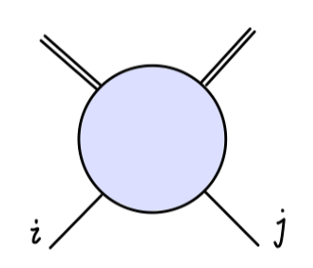
∼2iλ2δij(N+8)(4π)2Γ(2−2d)
考虑对应的 counterterm:
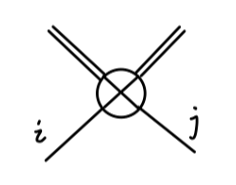
其值为:
∼−2iδijδλ=−2iδijλ2(N+8)(4π)2Γ(2−2d)
可以发现,发散确实消去了,对于 σσππ 顶点,我们将计算得到有限值。
4π 顶点
对 4π 顶点的一阶修正圈图为:
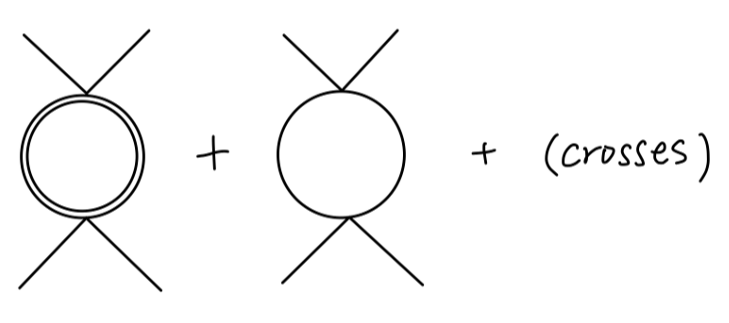
第一个图为 σ-loop:
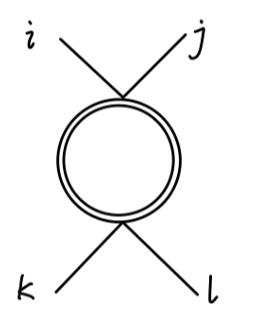
其值是:
∼21⋅(−2iλδij)(−2iλδkl)⋅(4π)2−iΓ(2−2d)=2iλ2δijδkl(4π)2Γ(2−2d)
第二个图为 π-loop:
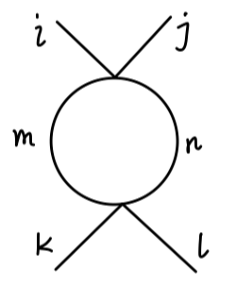
其值是:
∼21⋅(−2iλ(δijδmn+δimδjn+δinδjm))⋅(−2iλ(δklδmn+δkmδln+δknδlm))⋅(4π)2−iΓ(2−2d)=2iλ2((N+3)δijδkl+2δikδjl+2δilδjk)(4π)2Γ(2−2d)
对于每一个图,都有 s,t,u 三个 channel 的图,它们的值除了指标 ijkl 的配对情况外是相同的。最终的结果应当是每一个 δ 因子项前的系数均相同,最终得到 4π 顶点的值为:
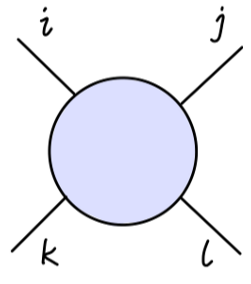
∼2iλ2(δijδkl+δikδjl+δilδjk)(N+8)(4π)2Γ(2−2d)
对应的 counterterm 为:
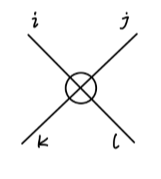
其值为:
∼−2iδλ(δijδkl+δikδjl+δilδjk)=−2iλ2(δijδkl+δikδjl+δilδjk)(N+8)(4π)2Γ(2−2d)
我们验证了 4π 顶点的紫外发散也会消去。
3σ 顶点
对于 3σ 顶点的一阶修正为:
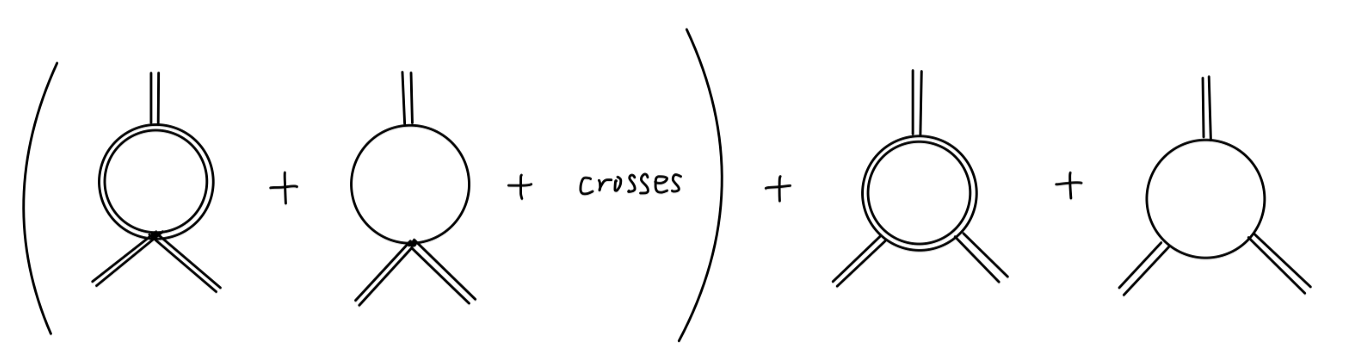
其中只有第一个图与第二个图是发散的(包含其他的channel)。
对于第一个 σ-loop 图:
其值为:
=21⋅(−6iλ)(−6iλv)⋅∫(2π)dddkk2−2μ2i(k+p)2−2μ2i18iλ2v(4π)2Γ(2−2d)
对于第二个 π-loop 图:
其值为:
∼2iλ2v(N−1)(4π)2Γ(2−2d)
对于其他两个 channel,得到的值将相等。最终得到 3σ 顶点的发散部分为:
其值为:
∼6iλ2v(N+8)(4π)2Γ(2−2d)
3σ 顶点的 counterterm 为:
其值为:
∼−6iδλv=−6iλ2v(N+8)(4π)2Γ(2−2d)
可以得到 3σ 顶点的发散将消去。对于 σππ 顶点来说,我们也可以进行类似于 σσππ 顶点的计算,最终的发散也会消去,得到下图将会为有限值,此处不进行过多讨论。
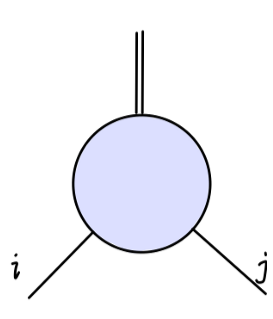
一点关联函数与两点关联函数
重整化条件:σ 一点关联函数
现在我们利用 4σ 顶点,根据重整化条件确定 δλ,成功地消除了所有三点关联函数与四点关联函数中的发散。现在我们来处理一点关联函数与两点关联函数。
根据重整化条件,我们选取如下 σ 一点关联函数的值为 0:
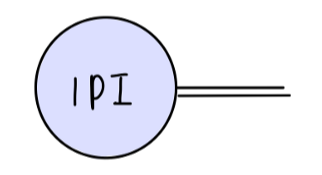
考虑到一阶圈图修正与 counterterm,将以上重整化条件写为:
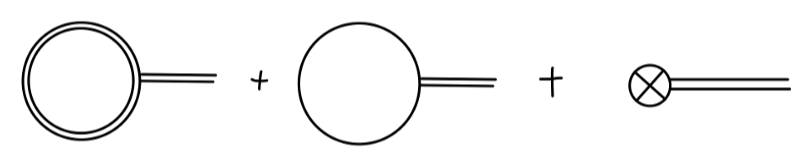
其值为零。
其中包含 σ-loop 的图为:
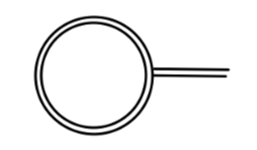
其值为:
=21(−6iλv)∫(2π)dddkk2−2μ2i−3iλv(4π)d/2Γ(1−2d)(2μ21)1−2d
对于第二个包含 π-loop 的图;
由于含有一个无质量粒子的传播子,为了防止积分出现红外发散,我们为其添加一个小质量 ζ,得到:
=21(−2iλv)δij∫(2π)dddkk2−ζ2iδij−i(N−1)λv(4π)d/2Γ(1−2d)(ζ21)1−2d
对于上式来说,当 d>2 时,其值在 ζ=0 时消失。更奇怪的是,其出现了一个 d=2 的极点。Anyway,我们将上述两个图的值加起来就能将重整化条件写为:
(δμ+v2δλ)=−λ(4π)d/2Γ(1−2d)((2μ2)1−d/23+(ζ2)1−d/2N−1)(13)
重整化条件:2σ 图
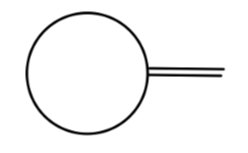
为了确定 δZ,我们还需要计算 2σ 图。根据重整化条件,我们选取如下 2σ 图在 p2=m2 的值为 0。
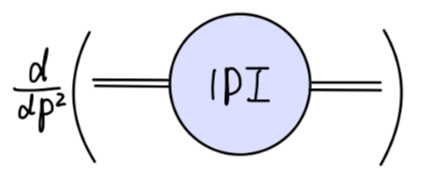
考虑一阶圈图与 counterterm 为:
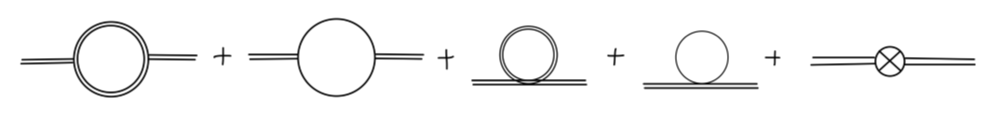
一般来说,σ 的质量还可能通过以下图发生 shift:
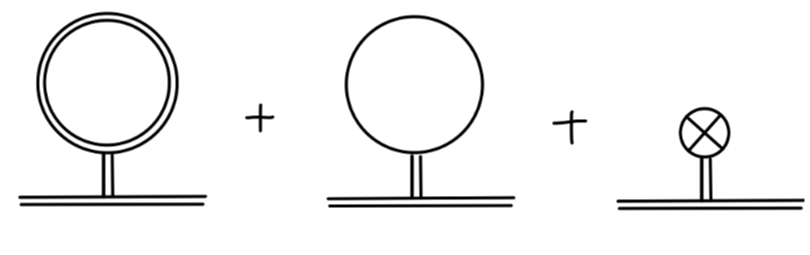
但通过第二个重整化条件,它们将是严格相消的,这也是我们如此选择重整化条件的好处之一。
为了方便讨论,我们将 counterterm 的值写为:
−i(2v2δλ)−i(δμ+v2δλ)+ip2δZ
现在进行 2σ 图的计算。
考虑第一个图:
其值为:
∼18iλ2v2(4π)2Γ(2−2d)
考虑第二个图:
其值为:
∼2iλ2v2(N−1)(4π)2Γ(2−2d)
可以发现这两个图的值加起来正好和 counterterm 的第一项相消去。对于第三、第四个图,根据第二个重整化条件,它们会和 counterterm 的第二项消去。最终我们将得到:δZ=0。
ππ 图
现在我们进行重整化后已经只剩下一种发散的图没有讨论了。这就是 ππ 图:
考虑一阶圈图与 counterterm 为:

其中第一个图为:
其值为:
=21(−2iλδij)∫(2π)dddkk2−2μ2i−iλδij(4π)d/2Γ(1−2d)(2μ21)1−2d
其中第二个图为:
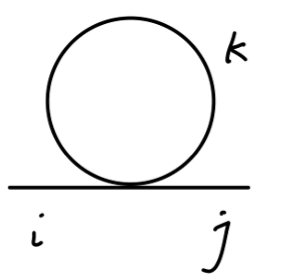
其值为:
=21(−2iλ(δijδkk+δikδjk+δikδjk))∫(2π)dddkk2−ζ21−iλ(N+1)δij(4π)d/2Γ(1−2d)(ζ21)1−2d
其中第三个图为:
其值为:
=(−2iλvδik)(−2iλvδkj)∫(2π)dddkk2−ζ2i(k+p)2−2μ2i4iλ2v2δij(4π)d/2Γ(2−2d)∫01dx(2μ2x+(1−x)ζ2−p2x(1−x)1)2−2d
考虑到其中发散的部分是独立于 p 的,不妨设置 p=0 方便后面的讨论。
对于 counterterm:
其值为:
=iδij(δZp2−δμ−δλv2)iλδij(4π)d/2Γ(1−2d)((2μ2)1−d/23+(ζ2)1−d/2N−1)
如此将以上四个图的贡献加起来,得到 ππ 图在 p=0 时的振幅:

其值为:
(−iλδij){(4π)d/2Γ(1−2d)((2μ2)1−2d1+(ζ2)1−d/2N+1)−4λv2(4π)d/2Γ(2−2d)∫01dx(2μ2x+(1−x)ζ21)2−2d−(4π)d/2Γ(1−2d)((2μ2)1−d/23+(ζ2)1−d/2N−1)}(14)
对上式进行化简,第一行与第三行相加得到:
2iλδij(4π)d/2Γ(1−2d)[(ζ2)1−d/21−(2μ2)1−d/21]
注意到方括号中的式子在 d=2 时相消,因此 d=2 时 Γ 函数的发散将会消失。只剩下了 d=4 的极点,我们可以将上式重写为:
2iλδij(4π)d/2Γ(2−2d)1−d/21[(ζ2)2−d/2ζ2−(2μ2)2−d/22μ2](15)
上式中第一项在 d>2,ζ→0 时,可以忽略。于此同时,(14) 式第二行成为:
ζ→0⟶iλδij4λv2(4π)d/2Γ(2−2d)d/2−11⋅2μ2−ζ2(2μ2)d/2−1−(ζ2)d/2−1iλδij4λv2(4π)d/2Γ(2−2d)d/2−11(2μ2)d/2−2(16)
考虑到 λv2=μ2,我们发现 (15)(16) 式正好消去,因此得到的 ππ 图在 p=0 时的振幅将会是一个有限值。