变换群

变换群与单参数变换群

变换群

微分同胚群
设 XX 是一个光滑流形。若 Φ:X→X\Phi : X \rightarrow X 是一个微分同胚，则称 Φ\Phi 是 XX 的一个 变换。我们可将 XX 的所有变换形成的集合记为 Diff(X)\mathrm{Diff}(X)。以映射的复合为乘法，Diff(X)\mathrm{Diff}(X) 形成一个群（恒元为恒等映射，逆映射存在保证逆元存在）。显然对于 XX 的一个变换，我们可以定义其在流形的光滑张量场上的推前和拖回映射 Φ∗\Phi_* 和 Φ∗\Phi^*。

在很多引力理论中, 我们要求作用量、拉氏量、以及运动方程等是 微分同胚变换不变的 (diffeomorphism invariant) 或 协变的 (covariant)。其意义就是要求它们的作用量、运动方程等在微分同胚变换下是不变的。

李氏变换群
假定 GG 是一个李群，而 XX 是一个光滑流形。设

Φ:G×X→X,(g,p)↦Φ(g,p)\Phi : G \times X \rightarrow X ,\quad (g,p) \mapsto \Phi(g,p)

是一个光滑映射。对每一个群元 gg，定义

Φg:X→X,p↦Φg(p)=Φ(g,p)\Phi_g : X \rightarrow X ,\quad p \mapsto \Phi_g (p) = \Phi(g,p)

若 Φg\Phi_g 满足：

  • Φe\Phi_e = IdX\mathrm{Id}_X，其中 ee 是 GG 的恒元
  • Φgh=Φg∘Φh, ∀g,h∈G\Phi_{gh} = \Phi_g \circ \Phi_h ,\ \forall g,h \in G（或 Φhg=Φg∘Φh, ∀g,h∈G\Phi_{hg} = \Phi_g \circ \Phi_h ,\ \forall g,h \in G）。

则称 GG 是左（或右）作用在光滑流形 XX 上的 变换群。

容易验证 {Φg,g∈G}\{\Phi_g,g\in G\} 的确成群，群乘法即为映射的复合，且有 Φg−1=(Φg)−1\Phi_{g^{-1}} = (\Phi_g)^{-1}，因此每一个 Φg\Phi_g 都存在逆映射，故它是 XX 的一个变换。

由以上定义可以看出下面的映射：

G→Diff(X),g→Φg∈Diff(X)G\rightarrow \mathrm{Diff}(X),\quad g\rightarrow \Phi_g\in \mathrm{Diff}(X)

是一个群同态，且 {Φg,g∈G}\{\Phi_g,g\in G\} 是微分同胚群 Diff(X)\mathrm{Diff}(X) 的一个子群。因此，粗略地说，关于李群 GG 的李变换群（若存在）使得我们能够以李群 GG 为模板在 Diff(X)\mathrm{Diff}(X) 中找出一个与其同构的子群。

群作用的轨道 (orbits)
设 Φ:G×X→X\Phi : G \times X \rightarrow X 是一李氏变换群，则称 {Φ(g,p)∣g∈G}\{\Phi(g,p)|g \in G\} 为群过 p∈Xp \in X 点的轨道，其中 gg 跑遍整个群 GG。

群作用的固定点集 (fixed points)
设 Φ:G×X→X\Phi : G \times X \rightarrow X 是一李氏变换群，则称 {p∣Φ(g,p)=p, ∀g∈G}\{p| \Phi(g,p) = p,\ \forall g \in G\} 为该群作用的固定点集。

迷向子群 (isotropy group)
设 Φ:G×X→X\Phi : G \times X \rightarrow X 是一李氏变换群，则称 {g∣Φ(g,p)=p}\{g| \Phi(g,p) = p\} 为该群作用在 pp 的迷向子集。

有效、自由、和可迁

  • GG 在 XX 上的作用称为 有效的（effective），若对 ∀p∈X, Φg(p)=p\forall p\in X,\ \Phi_g (p) = p 意味着 g=eg = e
  • GG 在 XX 上的作用称为 自由的（free），若除了 g=eg = e 之外，Φg(p)≠p\Phi_g (p)\neq p。
  • GG 在 XX 上的作用称为 可迁的（transitive），若对任意 p,q∈Xp,q \in X，总存在一个 g∈Gg \in G 使得 Φg(p)=q\Phi_g (p) = q。

有效意味着：流形上任意一点的迷向子群平庸。
自由意味着：没有固定点集。
可迁意味着：整个流形 XX 就是一个轨道。

例如考虑 SO(3)SO(3) 在 R3\mathbb{R}^3 上的作用。其固定点集为原点；除原点外任一点的轨道为一个球面；原点的迷向子群为 SO(3)SO(3)，除原点外任意点的迷向子群为 SO(3)SO(3) 群的一个 SO(2)SO(2) 子群。所以：SO(3)SO(3) 在 R3\mathbb{R}^3 上的作用不是有效，不是自由，也不是可迁的。

考虑 SO(3)SO(3) 在二维球面 S2S^2 上的作用：不是有效，但是自由，也可迁。

单参数变换群

有一种特殊的变换群，取 GG 为光滑的阿贝尔群 R\mathbb{R}. 设：

Φ:R×X→X,(t,p)↦Φ(t,p)\Phi : \mathbb{R} \times X \rightarrow X ,\quad (t,p)\mapsto \Phi(t,p)

是光滑映射。对每一个 t∈Rt \in R，定义：

Φt:X→X,p↦Φt(p)=Φ(t,p)\Phi_t : X \rightarrow X ,\quad p \mapsto \Phi_t (p) = \Phi(t,p)

若 Φt\Phi_t 满足：

  • Φ0=IdX,\Phi_0 = \mathrm{Id}_X ,
  • Φt+s=Φt∘Φs, ∀t,s∈R\Phi_{t+s} = \Phi_t \circ \Phi_s ,\ \forall t,s \in R

则称 Φ\Phi 是作用在光滑流形 XX 上的单参数变换群。显然，单参数变换群如果存在，则其在 Diff(X)\mathrm{Diff}(X) 中找出一个 1-维子群。

对于流形 XX 上的任意一点，我们可以定义光滑映射

Φp:R→X,t↦Φp(t)=Φ(t,p)\Phi_p: \mathbb{R} \rightarrow X,\quad t\mapsto \Phi_p(t) = \Phi(t,p)

这样，由单参数变换我们得到一条过 pp 的曲线，这条曲线称为单参数变换过 pp 的轨道。

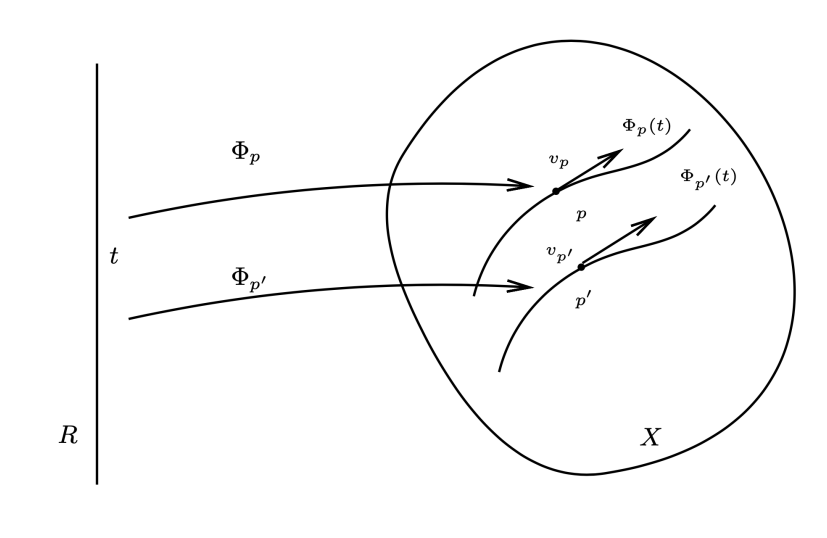
Φt\Phi_t 可表示为：

单参数变换群诱导的矢量场
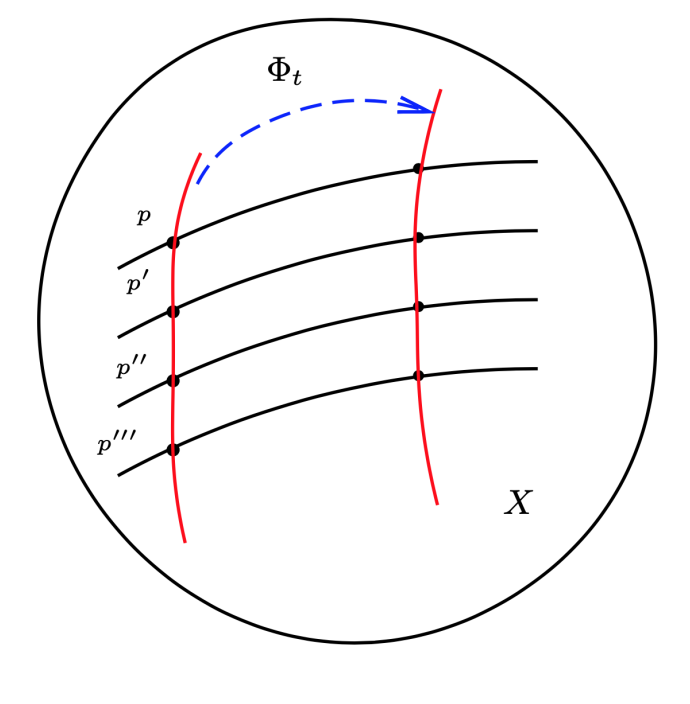
单参数变换群的轨道是流形上的曲线，因此由单参数变换群可以诱导出流形上的矢量场。

vp=d(Φp(t))idt∣t=0∂∂xi∣pv_p=\frac{d(\Phi_p(t))^i}{dt}|_ {t=0} \frac{\partial }{\partial x^i}| _ {p}

其中 (Φp(0))i=xi(p)(\Phi_p(0))^i = x^i(p) 为 pp 点的坐标函数，因此 Φp(t)\Phi_p(t) 是光滑的，故这个矢量场是光滑的。

单参数变换群的任意一条轨道是其诱导出的光滑矢量场的积分曲线。

设 q=Φp(s)=Φ(s,p)q = \Phi_p(s) = \Phi(s,p)，则我们有：

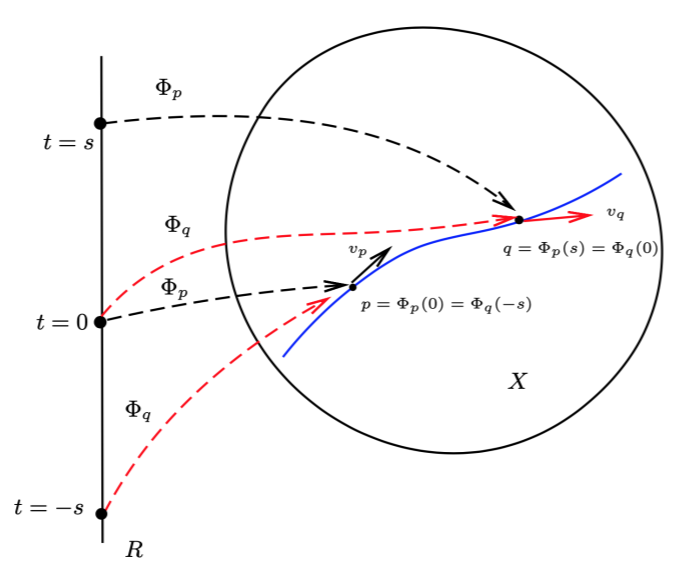
Φq(t)=Φ(t,q)=Φ(t,Φ(s,p))=Φt∘Φs(p)=Φt+s(p)=Φ(t+s,p)=Φp(t+s)\begin{aligned} \Phi_q(t) &= \Phi(t,q) = \Phi(t,\Phi(s,p)) = \Phi_t\circ \Phi_s(p)\\ &= \Phi_{t+s}(p) = \Phi(t+s,p) = \Phi_p(t+s) \end{aligned}

可见过 pp 点的轨道与过 qq 点的轨道在 XX 中的像是一样的，它们的不同在于曲线参数的选取不一样。

按照单参数变换诱导矢量场的定义，对于 XX 上的任意光滑函数ff，在 qq 点的切矢量为：

vq(f)=d(f∘Φq(t))dt∣t=0=d(f∘Φp(t+s))dt∣t=0=d(f∘Φp(t))dt∣t=s\begin{aligned} v_q(f) &= \frac{d (f\circ \Phi_{q}(t))}{dt}|_{t=0}\\ &= \frac{d(f\circ \Phi_p(t+s))}{dt}|_{t=0}\\ &= \frac{d(f\circ \Phi_p(t))}{dt}|_{t=s}\\ \end{aligned}

此式表明：vqv_{q} 恰是过 pp 点的轨道在 qq 点的切矢量，从而单参数变换群过 pp 的轨道是其诱导出的光滑切矢量场的积分曲线。

另外还有：

vq(f)=d(f∘Φp(t+s))dt∣t=0=d(f∘Φs∘Φp(t))dt∣t=0=vp(f∘Φs)=vp((Φs)∗(f))=(Φs)∗vp(f)\begin{aligned} v_q(f)&=\frac{d (f\circ \Phi_{p}(t+s))}{dt}|_{t=0}\\ &=\frac{d (f\circ \Phi_{s}\circ \Phi_p(t))}{dt}|_{t=0}\\ &=v_p(f\circ \Phi_s)\\ &=v_p((\Phi_s)^*(f))\\ &=(\Phi_s)_*v_p(f) \end{aligned}

于是得到：

(Φs)∗vp=vΦs(p)(\Phi_s)_*v_p = v_{\Phi_s(p)}

设 vv 是光滑流形 XX 上的光滑矢量场，而 Φ:X→X\Phi:X\rightarrow X 是一个变换，若 Φ∗v=v\Phi_*v = v，则称 vv 在变换 Φ\Phi 下不变，称为 不变矢量场。上式表明：单参数变换群的诱导切矢量场 vv 在单参数变换 {Φt,t∈R}\{\Phi_t,t\in\mathrm{R}\} 下不变。

李群的单参数子群

单参数子群
李群 GG 的 单参数子群（one parameter subgroup） 是 GG 上的一条可微曲线（这里我们考虑光滑的情况）：

R→G,t↦g(t)\mathbb{R} \rightarrow G, t \mapsto g(t)

且满足

g(t)g(s)=g(t+s),g(0)=eg(t)g(s) = g(t + s),\quad g(0) = e

Killing 矢量场
设 GG 是左作用在 XX 上的李群, 即我们有李变换群 {Φg,g∈G}\{\Phi g ,g \in G\} 李群 GG 的单参数子群生给出一个 XX 上的单参数变换群

{Φg(t),t∈R}⊂Diff(X)\{\Phi_{g(t)} ,t \in R\} \subset \mathrm{Diff}(X)

由此单参数变换群，可以得到其诱导切矢量场。这个矢量场称为流形 XX 上相对于李群 GG 的 Killing 矢量场（基本切矢量场）。

由前面的讨论，我们发现：由一个单参数变换，我们可以得到流形上的一个矢量场。但反过来，由流形上的一个矢量场，我们并不一定能够得到一个关于这个流形的单参数变换。但是它可以生成所谓的局部单参数变换（伪）群。

局部单参数变换群

局部单参数变换（伪）群
设 UU 是光滑流形 XX 的一个开集。若光滑映射

Φ:(−ϵ,ϵ)×U→X,ϵ>0\Phi : (-\epsilon,\epsilon) \times U \rightarrow X ,\quad \epsilon > 0

满足：对任意 p∈U,∣t∣<ϵp \in U, |t| < \epsilon 有：

  • Φ0=IdU\Phi_0 = \mathrm{Id}_U
  • 如果 ∣s∣,∣t∣,∣t+s∣<ϵ|s|,|t|,|t + s| < \epsilon 且 p,Φt(p)∈Up,\Phi_t (p) \in U，存在

Φs∘Φt(p)=Φt+s(p)\Phi_ s \circ \Phi_t(p) = \Phi_ {t+s} (p)

这里，和前面单参数变换的情况一样，我们定义了：

Φt(p)=Φ(t,p)\Phi_t (p) = \Phi(t,p)

定理：
设 vv 是光滑流形 XX 上的光滑切矢量场，则对于任意一点 p∈Xp \in X，存在一个邻域 N(p)N(p) 和一个作用在 N(p)N(p) 上的局部单参数变换群 {Φt,∣t∣<ϵ}\{\Phi_t ,|t| < ϵ\} 使得矢量场 vv 在 N(p)N(p) 上的限制，即：v∣N(p)v|_ {N(p)} 是这个局部单参数变换群的诱导切矢量场。

定理：

设 XX 是紧致的光滑流形，则 XX 上的任意一个光滑切矢量场生成一个单参数变换群。即存在一个单参数变换群使得它的诱导切矢量场恰好是这个给定的切矢量场。

李导数

切矢量场的李导数（Lie derivative）

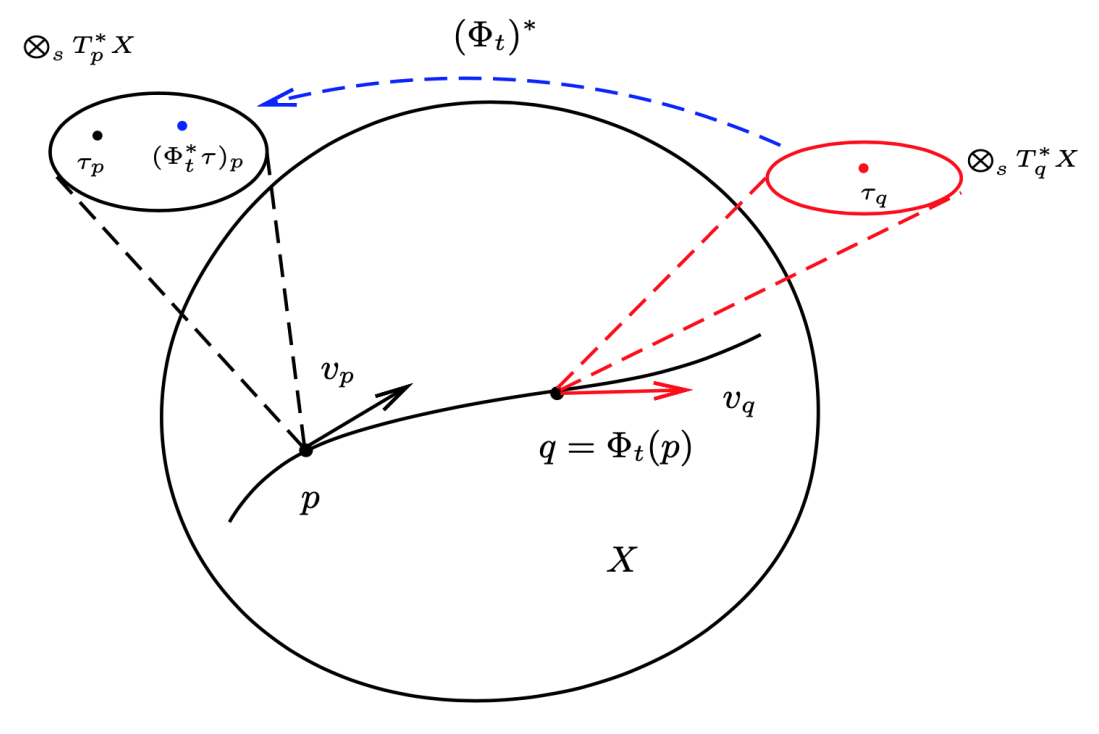
设 vv 和 uu 是光滑流形 XX 上的两个光滑矢量场。vv 在 pp 点的邻域 N(p)N(p) 生成的局部单参数变换记为 Φt\Phi_ t。切矢量场 uu 沿着切矢量场 vv 在 pp 点的李导数定义为：

Lvu∣p=lim⁡t→0(Φ−t)∗uΦt(p)−upt\mathcal{L}_vu| _ p=\lim_{t\rightarrow 0}\frac{(\Phi_{-t})_ * u_{\Phi_{t}(p)}-u_p}{t}

其中推前映射 (Φ−t)∗(\Phi_{-t})_* 将 q=Φt(p)q = \Phi_t(p) 点的切矢量 uqu_q 推到 pp 点处，因为只有相同点的切矢量才可以进行差运算。示意图如下：

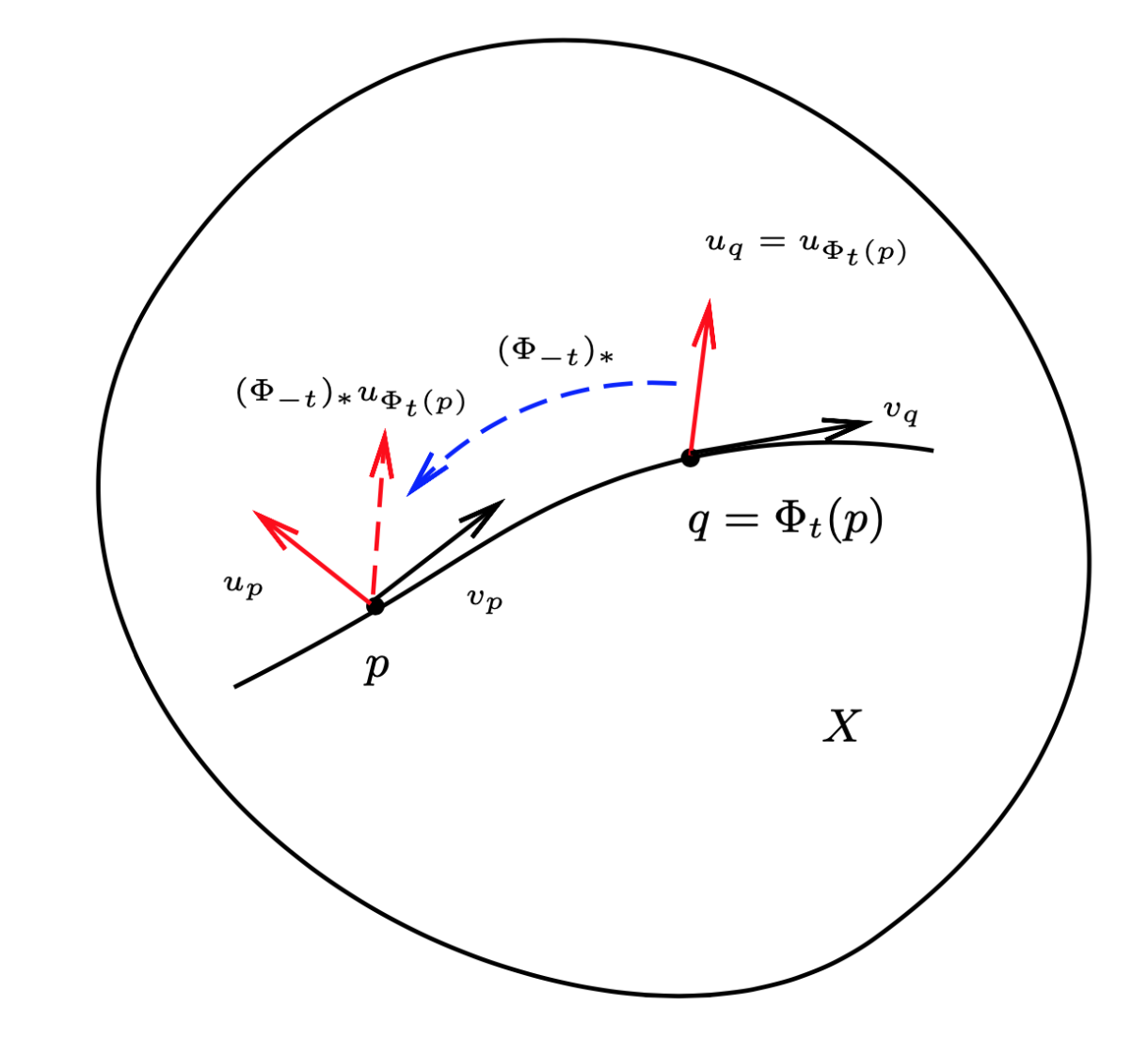
可以证明：

Lvu∣p=[v,u]∣p.\mathcal{L}_v u| _ p = [v,u]|_ p .

上面的讨论和定理对于流形上的任意一点 pp 都是成立的，因此可以将定义进行改写。
切矢量场 uu 沿着切矢量场 vv 的李导数定义为：

Lvu=lim⁡t→0(Φ−t)∗u−ut=[v,u]\mathcal{L}_vu=\lim_{t\rightarrow 0}\frac{(\Phi_{-t}) _ * u-u}{t}=[v,u]

其中 Φt\Phi_t 是由切矢量场 vv 生成的局部单参数变换群。

可见，Lv\mathcal{L}_v 是一个映射：

Lv:X(X)→X(X)\mathcal{L}_v: \mathscr{X}(X) \rightarrow \mathscr{X}(X)

它将一个切矢量场变成另一个切矢量场。李导数 反映了一个切矢量场沿着另一个切矢量场（的积分曲线）的变化率。

对于光滑函数来说，有：

v(f)∣p=d(f∘Φp(t))dt∣t=0=d(f∘Φt(p))dt∣t=0=ddt((Φt)∗f)(p)∣t=0=lim⁡t→0((Φt)∗f)(p)−f(p)t=Lvf\begin{aligned} v(f)|_{p} &= \frac{d(f\circ \Phi_p(t))}{dt}|_{t=0}\\ &= \frac{d(f\circ \Phi_t(p))}{dt}|_{t=0}\\ &= \frac{d}{dt}((\Phi_t)^*f)(p)|_{t=0}\\ &=\lim_{t\rightarrow 0} \frac{((\Phi_t)^*f)(p)-f(p)}{t}\\ &=\mathcal{L}_{v}f\\ \end{aligned}

协变张量的李导数
设 τ\tau 是 s−s- 阶协变张量场，v∈X(X)v \in \mathscr{X} (X)，而 Φt\Phi_ t 是由 vv 生成的局部单参数变换。则 τ\tau 关于切矢量场 vv 的李导数定义为：

Lvτ=lim⁡t→0(Φt)∗τ−τt\mathcal{L}_v\tau=\lim_{t\rightarrow 0}\frac{(\Phi_t)^* \tau-\tau}{t}

逆变张量的李导数
设 τ\tau 是 ss-阶逆变张量场，v∈X(X)v \in X (X)，而 Φt\Phi_t 是由 vv 生成的局部单参数变换. 则 τ\tau 关于切矢量场 vv 的李导数定义为：

Lvτ=lim⁡t→0(Φ−t)∗τ−τt\mathcal{L}_v\tau=\lim_{t\rightarrow 0}\frac{(\Phi_{-t})_ * \tau-\tau}{t}

不管是 $(\Phi_t)^* $，还是 (Φ−t)∗(\Phi_{-t})_*，或是统一简写为 (Φt)∗(\Phi_t)^*，它们都是由微分同胚 Φt\Phi_t 诱导出的线性同构映射。因此，我们可以很自然的定义一般的 (r,s)(r, s)-型张量场 τ\tau 的李导数为：

Lvτ=lim⁡t→0(Φt)∗τ−τt\mathcal{L}_v\tau=\lim_{t\rightarrow 0}\frac{(\Phi_t)^* \tau-\tau}{t}

可以看出：李导数把一个张量场变成同一类型的张量场。

由拖回映射和推前映射的线性、与张量积可交换性、以及和缩并运算的可交换性，我们可得到李导数的如下性质：

  • R−\mathbb{R}- 线性：∀λ1,λ2∈R\forall \lambda_ 1 ,\lambda_ 2\in \mathbb{R}，相同类型的张量 τ1,τ2\tau_ 1 , \tau_ 2 我们有

Lv(λ1τ1+λ2τ2)=λ1Lvτ1+λ2Lvτ2\mathcal{L}_v (\lambda_ 1 \tau_ 1 + \lambda_ 2 \tau_ 2 ) = \lambda_ 1 \mathcal{L}_ v \tau_ 1 + \lambda_ 2 \mathcal{L}_ v \tau_ 2

  • Leibniz 法则：设 τ1\tau_ 1 和 τ2\tau_ 2 是两个张量场，它们的类型可以不同。我们有：

Lv(τ1⊗τ2)=(Lvτ1)⊗τ2+τ1⊗(Lvτ2)\mathcal{L}_ v (\tau_ 1 \otimes \tau_ 2 ) = (\mathcal{L}_ v \tau_ 1 ) \otimes \tau_ 2 + \tau_ 1 \otimes(\mathcal{L}_ v \tau_ 2)

  • 和缩并可交换：

Lv∘C(τ)=C∘Lv(τ)\mathcal{L}_ v \circ C(\tau) = C \circ \mathcal{L}_ v (\tau)

局部坐标下的表示

设在某个坐标卡下，光滑切矢量场 vv 可表示为 v=vi∂∂xiv = v^i\frac{\partial}{\partial x^i}。

对 f∈F(X)f\in \mathscr{F}(X)，得到：

Lvf=v(f)=vi∂f∂xi\mathcal{L}_vf = v(f) = v^i\frac{\partial f}{\partial x^i}

对自然基 ∂∂xi\frac{\partial }{\partial x^i}，有

Lv∂∂xi=[v,∂∂xi]=−∂vj∂xi∂∂xj\mathcal{L}_v\frac{\partial}{\partial x^i}=[v,\frac{\partial}{\partial x^i}]=-\frac{\partial v^j}{\partial x^i}\frac{\partial}{\partial x^j}

对于对偶基 dxidx^i，我们有

C∘Lv(dxi⊗∂∂xj)=Lv∘C(dxi⊗∂∂xj)=Lvδ  ji=0C\circ \mathcal{L}_v(dx^i\otimes \frac{\partial}{\partial x^j}) = \mathcal{L}_v\circ C(dx^i\otimes \frac{\partial}{\partial x^j}) = \mathcal{L}_v \delta^i_{\ \ j} = 0

根据李代数的性质有：

0=C(Lvdxi⊗∂∂xj+dxi⊗Lv∂∂xj)=C(Lvdxi⊗∂∂xj−∂vk∂xjdxi⊗∂∂xk)\begin{aligned} 0 &= C(\mathcal{L}_v dx^i\otimes \frac{\partial}{\partial x^j} + dx^i\otimes \mathcal{L}_v\frac{\partial}{\partial x^j})\\ &= C(\mathcal{L}_v dx^i\otimes \frac{\partial}{\partial x^j} - \frac{\partial v^k}{\partial x^j} dx^i\otimes \frac{\partial}{\partial x^k})\\ \end{aligned}

从而有：

C(Lvdxi⊗∂∂xj)=∂vi∂xjC(\mathcal{L}_v dx^i\otimes \frac{\partial}{\partial x^j}) = \frac{\partial v^i}{\partial x^j}

设 Lvdxi=A  kidxk\mathcal{L}_v dx^i = A^i_{\ \ k}dx^k，则由上式得到：

A  ji=∂vi∂xjA^i_{\ \ j} = \frac{\partial v^i}{\partial x^j}

如此得到李代数作用于对偶基的结果：

Lvdxi=∂vi∂xjdxj\mathcal{L}_v dx^i=\frac{\partial v^i}{\partial x^j}dx^j

这样，利用李代数作用于光滑函数，自然基和其对偶基的结果，我们可以得到任意一个光滑张量场关于 vv 的李导数的局部坐标表示。

李导数其他性质
设 u,v∈X(X), f∈F(X)u,v \in \mathscr{X} (X),\ f \in \mathscr{F}(X)， 则有：

  • Lu+v=Lu+Lv\mathcal{L}_ {u+v} = \mathcal{L}_ {u}+\mathcal{L}_ {v}
  • L[u,v]=Lu∘Lv−Lv∘Lu\mathcal{L}_ {[u,v]} = \mathcal{L}_ {u}\circ \mathcal{L}_ {v}-\mathcal{L}_ {v} \circ \mathcal{L}_ {u}
  • Lfvu=[fv,u]=fLvu−u(f)v\mathcal{L}_ {fv} u = [fv,u] = f\mathcal{L}_ v u - u(f)v

利用李导数与李括号的关系，上述式子是不难证明的。

微分同胚变换与坐标变换

这一部分的目的：明确微分同胚变换 Φ:X→X\Phi:X\rightarrow X 和 XX 上的坐标变换的关系。

微分同胚的两种理解

  • 主动观点（active viewpoint）：点发生变化，即 Φ:p→Φ(p)\Phi : p \rightarrow \Phi(p)，张量 τp\tau_p 被映射到 Φ(p)\Phi(p) 点的张量 Φ∗pτp\Phi_{* p} \tau_p 。在这种观点下，XX 上的张量场 τ\tau 在微分同胚变换下变成 XX 上的另外一个张量场 Φ∗τ\Phi_ {*} \tau，即

τ→Φ∗τ\tau \rightarrow \Phi_ * \tau

这一定义与坐标和张量的分量没有直接关系。

  • 被动观点（passive viewpoint）：
    点没有发生变化，而认为 Φ\Phi（对张量）的作用是对“张量分量” 做了一个坐标变换。张量 τp\tau_ p 的分量在这个坐标变换后恰好等于主动观点中 Φ∗pτp\Phi_ {*p} \tau_ p 的分量。在这一观点下，张量的分量是重要的。

微分同胚变换不变的物理量
若建立在流形 XX 上的一个物理或数学理论中由张量 τ,σ⋯\tau ,\sigma \cdots 等所组成物理量或数学量 G(τ,σ,⋯ )\mathscr{G}(\tau,\sigma ,\cdots) 在微分同胚变换下满足

G(Φ∗τ,Φ∗σ,⋯ )=Φ∗G(τ,σ,⋯ ), ∀Φ∈Diff(X)\mathscr{G}(\Phi_ * \tau ,\Phi_ * \sigma ,\cdots) = \Phi_ * \mathscr{G}(\tau ,\sigma ,\cdots),\quad\ \forall\Phi \in \mathrm{Diff(X)}

则我们称这个量是 微分同胚变换不变的（diffeomorphism invariant）。

微分同胚变换不变和广义协变
上面的微分同胚变换不变可以描述为

Gj1⋯jni1⋯im(τ~j1⋯jsi1⋯ir,σ~j1⋯jqi1⋯ip,⋯ )=G~j1⋯jni1⋯im(τj1⋯jsi1⋯ir,σj1⋯jqi1⋯ip,⋯ )\mathscr{G}^{i_1\cdots i_m}_{\qquad j_1\cdots j_n}(\tilde{\tau}^{i_1\cdots i_r}_{\qquad j_1\cdots j_s},\tilde{\sigma}^{i_1\cdots i_p}_{\qquad j_1\cdots j_q},\cdots)=\tilde{\mathscr{G}}^{i_1\cdots i_m}_{\qquad j_1\cdots j_n}(\tau^{i_1\cdots i_r}_{\qquad j_1\cdots j_s},\sigma^{i_1\cdots i_p}_{\qquad j_1\cdots j_q},\cdots)

因此，这实质上就是要求该物理量或数学量在坐标变换下是广义协变的。

上述讨论对流形 XX 上任意的微分同胚都成立. 若存在一些“特殊的”微分同胚 Φ\Phi 使得：

G(Φ∗τ,Φ∗σ,⋯ )=G(τ,σ,⋯ )\mathscr{G}(\Phi_ * \tau ,\Phi_ * \sigma ,\cdots) = \mathscr{G}(\tau ,\sigma ,\cdots)

我们称 Φ\Phi 是使得 G\mathscr{G} 保持不变的 对称性变换。

我们说微分同胚 Φ\Phi 是保持张量 τ\tau 不变的对称变换若

Φ∗τ=τorΦ∗τ=τ\Phi_* \tau = \tau\quad or\quad \Phi^* \tau =\tau

这等价于说在 Φ\Phi 诱导的坐标变换下 τ\tau 的分量满足

τ~j1⋯jsi1⋯ir=τj1⋯jsi1⋯ir\tilde{\tau}^{i_1\cdots i_r}_{\qquad j_1\cdots j_s}=\tau^{i_1\cdots i_r}_{\qquad j_1\cdots j_s}

微分同胚变换可以看成是一种坐标变换，任意一个光滑切矢量场 vav^ a 生成的局部单参数变换也可以理解成是一种与 vav^ a 相关的坐标变换。这就是所谓的 无穷小坐标变换。

Φt\Phi_ t 所对应的无穷小坐标变换可以写为：

x~i=xi+tvi\tilde{x}^ i = x^ i + tv^i

这就是人们常用的由切矢量场 vav_ a 生成的无穷小坐标变换的写法.若将上面的 Φt\Phi_ t 换为 Φ−t\Phi_{ -t}，立即可得相应的无穷小坐标变换为：

x~i=xi−tvi\tilde{x}^ i = x^ i - tv^i

现在考虑一些“特殊的”切矢量场 vav^a，它们生成的局部单参数变换 Φt\Phi_t是保持 τ\tau 不变的对称性变换。这意味着：

Lvτ=0\mathcal{L}_v\tau = 0

即：

0=vi∂iτj1⋯jsi1⋯ir−(∂kvi1)τj1⋯jski2⋯ir−(∂kvir)τj1⋯jsi1⋯k+(∂j1vl)τlj2⋯jsi1⋯ir−(∂jsvl)τj1⋯js−1li1⋯ir\begin{aligned} 0 =& v^i\partial_i\tau^{i_1\cdots i_r}_{\qquad j_1\cdots j_s}\\ &-(\partial_k v^{i_1})\tau^{ki_2\cdots i_r}_{\qquad j_1\cdots j_s}-(\partial_k v^{i_r})\tau^{i_1\cdots k}_{\qquad j_1\cdots j_s}\\ &+(\partial_{j_1} v^{l})\tau^{i_1\cdots i_r}_{\qquad lj_2\cdots j_s}-(\partial_{j_s} v^{l})\tau^{i_1\cdots i_r}_{\qquad j_1\cdots j_s-1l}\\ \end{aligned}

给出了有关 viv^i 的方程。