微分形式与外微分

微分形式

ss-阶全反对称张量为 ss-形式。这些 ss-形式（s=0,1⋯s = 0,1\cdots）形成外代数。

在光滑流形 XX 的每一点 pp，由该点的切空间 TpXT_ p X 和余切空间 Tp∗XT^ *_ p X，我们可以构造出该点的张量代数。同样，我们也可得到该点 ss-形式形成的线性空间 Λs(TpX)\Lambda_s (T_p X)，进而得到该点的外代数

Λ(TpX)=⨁s=0dim⁡(X)Λs(TpX)\Lambda(T_ p X) = \bigoplus_{s=0}^{\dim (X)}\Lambda_ s (T_ p X)

在 XX 上的每一点“光滑地”指定一个 ss-形式，我们便得到光滑的 ss-形式场，或简称为 ss-形式。XX 上所有的 ss-形式场的集合记为 Λs(X)\Lambda_ s (X)。

我们可以逐点定义加法和数乘，Λs(X)\Lambda_s(X) 形成光滑函数环 F(X)\mathscr{F}(X) 上的模，其中的 Λ1(X)\Lambda_1(X) 在前面我们已经遇到，它是流形上的光滑 11-形式场或余切矢量场的集合。这样，我们可以得到光滑形式场所形成的模：

Λ(X)=⨁s=0dim⁡(X)Λs(X)\Lambda(X) = \bigoplus_{s=0}^{\dim (X)}\Lambda_ s (X)

我们可以通过逐点定义，将 Λ(TpX)\Lambda(T_pX) 上的外积 ∧\land 推广到 Λ(X)\Lambda(X)，使之成为一个代数。

设 ω\omega 是一个 ss-形式，在某个局部坐标卡下，它可以表示为：

ω=1s!ωi1⋯isdxi1∧⋯∧dxis\omega = \frac{1}{s!}\omega_{i_1\cdots i_s}dx^{i_1}\land \cdots \land dx^{i_s}

其中 ωi1⋯is\omega_{i_1\cdots i_s} 是流形上的光滑函数。考虑坐标变换 xi→x~ix^i \rightarrow \tilde{x}^i，这些分量的变换规律为：

ωi1⋯is=∂x~j1∂xi1⋯∂x~js∂xisω~j1⋯js\omega_{i_1\cdots i_s} = \frac{\partial \tilde{x}^{j_1}}{\partial x^{i_1}}\cdots\frac{\partial \tilde{x}^{j_s}}{\partial x^{i_s}}\tilde{\omega}_{j_1\cdots j_s}

外微分

外代数上的阶化算子
设 O:Λ(X)→Λ(X)\mathcal{O} : \Lambda(X) \rightarrow \Lambda(X) 是一个 R\mathbb{R}-线性映射，使得：

O(Λs(X))⊂Λs+p(X)\mathcal{O}(\Lambda_ s (X)) \subset \Lambda_ {s+p} (X)

  • 若 O\mathcal{O} 满足：

O(ω∧θ)=O(ω)∧θ+ω∧O(θ)\mathcal{O}(\omega \land \theta) = \mathcal{O}(\omega) \land \theta + \omega \land \mathcal{O}(\theta)

则称 O\mathcal{O} 是 Λ(X)\Lambda(X) 上一个度数为 pp 的 导子(derivation with a degree pp)。

  • 若 O\mathcal{O} 满足：

O(ω∧θ)=O(ω)∧θ+(−1)deg⁡(ω)ω∧O(θ)\mathcal{O}(\omega \land \theta) = \mathcal{O}(\omega) \land \theta +(-1)^{\deg(\omega)} \omega \land \mathcal{O}(\theta)

则称 O\mathcal{O} 是 Λ(X)\Lambda(X) 上一个度数为 pp 的 反（阶化）导子 (antiderivation, graded derivation)。
其中 deg⁡(ω)\deg(\omega) 是指微分形式 ω\omega 的阶数。

设 ω\omega 是一个光滑的 ss-形式。粗略地说，外微分算子，记为 dd，将 ω\omega 变成一个光滑的 (s+1)(s + 1)-形式，并记为 dωd\omega。

具体来说，外微分算子是一个映射: d:Λ(X)→Λ(X)d : \Lambda(X) \rightarrow \Lambda(X)，使得 d(Λs(X))⊂Λs+1(X)d(\Lambda_ s (X)) \subset \Lambda_ {s+1} (X)
并满足

  • R\mathbb{R}-线性性：对任意 ω,θ∈Λ(X),λ∈R\omega,\theta \in \Lambda(X), \lambda\in R，要求

d(ω+θ)=dω+dθ,d(λω)=λdωd(\omega + \theta) = d\omega + d\theta,\quad d(\lambda\omega) = \lambda d\omega

  • 反（阶化）Leibniz 法则（anti-Leibniz, graded Leibniz）：

d(ω∧θ)=dω∧θ+(−1)deg⁡(ω)ω∧dθd(\omega\land \theta) = d\omega\land \theta+ (-1)^ {\deg(\omega)}\omega\land d\theta

  • 幂零性（Nilpotency）

d2=d∘d=0d^2 = d \circ d = 0

  • 对任意 f∈F(X)=Λ0(X)f \in \mathscr{F}(X) = \Lambda_0 (X)，dfdf 是 ff 的微分。

可以得到：外微分算子是一个度数为 “1” 的反导子。可以进一步证明，以上定义的外微分算子将是唯一的。

在局部坐标下，设 (U,φ)(U,\varphi) 是 XX 上的一个坐标卡，坐标为 xix^i，则 ss-形式 ω\omega 可以表示为：

ω=1s!ωi1⋯isdxi1∧⋯∧dxis\omega = \frac{1}{s!}\omega_{i_1\cdots i_s}dx^{i_1}\land \cdots \land dx^{i_s}

则有：

dω=1s!∂ωi1⋯is∂xidxi1∧⋯∧dxisd\omega = \frac{1}{s!}\frac{\partial \omega_{i_1\cdots i_s}}{\partial x^i}dx^{i_1}\land \cdots \land dx^{i_s}

设 Φ:X→Y\Phi : X \rightarrow Y 是流形 XX 到流形 YY 的光滑映射。则 Φ∗\Phi^* 是由 Λ(Y)\Lambda (Y) 到 Λ(X)\Lambda(X) 的线性映射，且可知 Φ∗\Phi^* 是一个线性同态。设 ω∈Λ(Y)\omega \in \Lambda(Y )，则可以证明

d(Φ∗ω)=Φ∗(dω)d(\Phi^ * \omega) = \Phi^ * (d\omega)

从而 d∘Φ∗=Φ∗∘dd \circ \Phi^ * = \Phi^* \circ d，即外微分算子和拖回映射可交换。

还有一些其他的算子可以看作阶化算子。

李导数
设 v∈X(X)v \in \mathscr{X} (X)，由李导数的 Leibniz 法则，我们知道：

Lv(ω∧θ)=Lvω∧θ+ω∧Lvθ\mathcal{L}_ v (\omega \land \theta) = \mathcal{L}_ v \omega \land \theta + \omega \land \mathcal{L}_ v \theta

又因为李导数不改变张量类型，因此李导数是 Λ(X)\Lambda(X) 上度数为 00 的导子。

内乘算子 (inner product)
设 v∈X(X)v \in \mathscr{X} (X)，内乘 ivi_ v 算子是一个线性算子：

iv:Λ(X)→Λ(X)i_ v : \Lambda(X) \rightarrow \Lambda(X)

使得 iv(Λs(X))⊂Λs−1(X)i_ v (\Lambda_ s (X)) \subset \Lambda_ {s-1} (X)，定义为

(ivω)(u1,⋯ ,us−1)=ω(v,u1,⋯ ,us−1)(i_v \omega)(u_ 1 ,\cdots ,u_ {s-1} ) = \omega(v,u_ 1 ,\cdots ,u_ {s-1})

其中

ui∈X(X),i=1,⋯−1,ω∈Λs(X)u_i \in \mathscr{X}(X), i = 1,\cdots - 1, \omega \in \Lambda_s (X)

若 ω∈Λ0(X),ivω=0\omega \in \Lambda_ 0 (X), i_v \omega = 0
可以证明

iv(ω∧θ)=(ivω)∧θ+(−1)deg⁡(ω)ω∧(ivθ)i_v (\omega \land \theta) = (i_ v \omega) \land \theta + (-1)^ {\deg(\omega)} \omega \land (i v \theta)

因此 ivi_ v 是一个度数为 −1-1 的反导子。

还可证明 ivi_ v 满足幂零性

iv2=iv∘iv=0i^ 2_v= i_v \circ i_ v = 0

李导数、内乘、和外微分满足：

Lv=iv∘d+d∘iv\mathcal{L}_v = i_ v \circ d + d \circ i_ v

这称为 Cartan formula。

由此定理，可知：对 nn-维流形上的 nn-形式 ω\omega，我们有

Lvω=d(ivω)\mathcal{L}_v \omega = d(i_ v \omega)

de Rham 上同调

外代数 Λ(X)\Lambda(X) 和外微分算子形成一个 de Rham 复形，通常可以表示为：

{0}⟶dΛ0(X)⟶dΛ1(X)⟶dΛ2(X)⟶d⋯⟶dΛn(X)⟶d{0}\{0\}\overset{d}{\longrightarrow}\Lambda_0(X)\overset{d}{\longrightarrow}\Lambda_1(X)\overset{d}{\longrightarrow}\Lambda_2(X)\overset{d}{\longrightarrow}\cdots\overset{d}{\longrightarrow}\Lambda_n(X)\overset{d}{\longrightarrow}\{0\}

其中我们已添加了两个实际上不存在的空间 Λ−1(X)\Lambda_{-1} (X) 和 Λn+1(X)\Lambda_ {n+1} (X)，它们都被假定为平庸空间 {0}\{0\}。

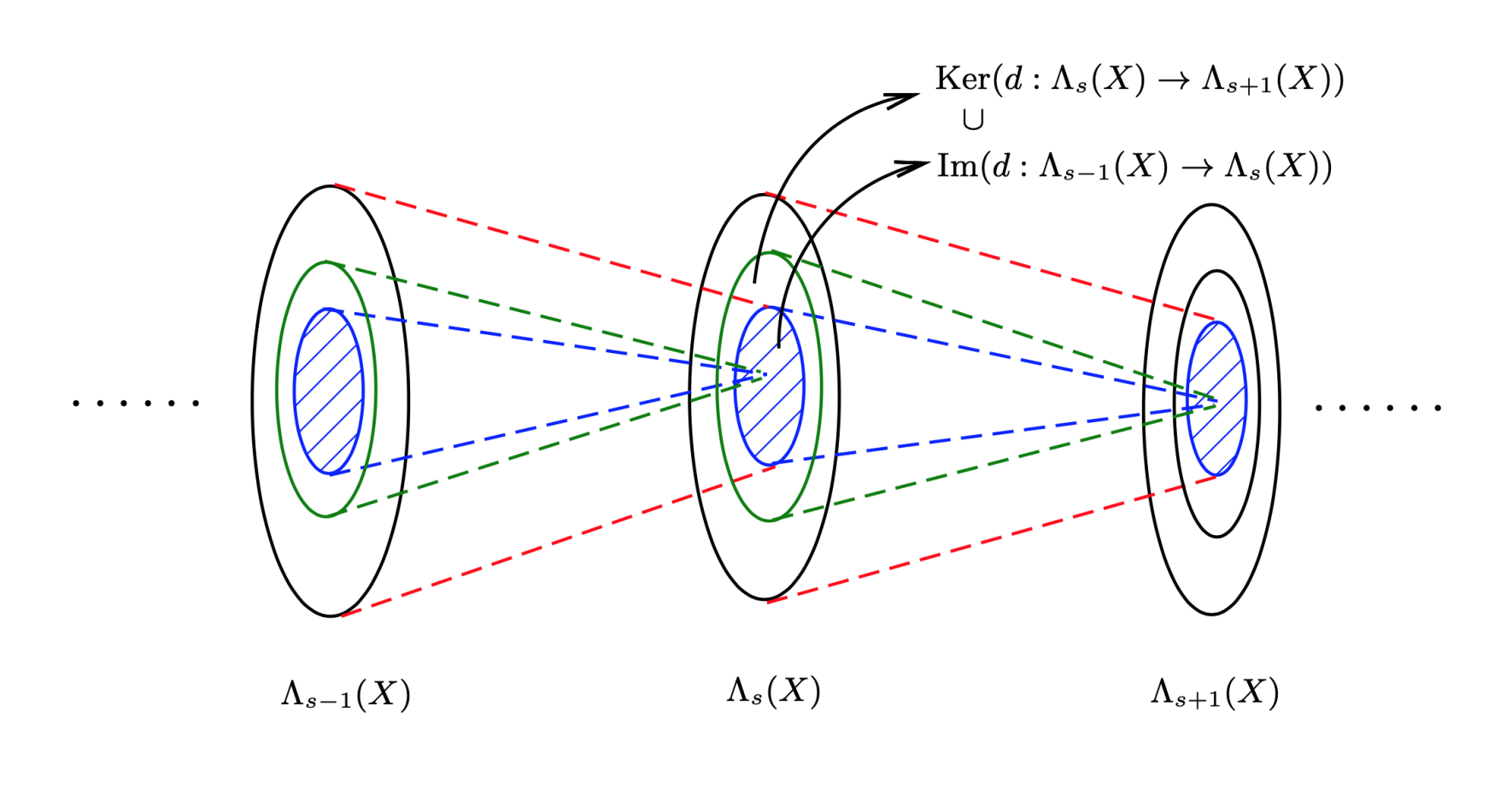
外代数 Λ(X)\Lambda(X) 和其上的外微分算子 dd 形成一个 可微阶化代数，自然地给出一个 de Rham 复形。所谓的 上同调理论 便是建立在类似的这样的序列之上。下我们做一点简单的介绍。

闭形式和恰当形式

  • 闭形式 (closed)
    设 ω∈Λ(X)\omega \in \Lambda(X)，若 dω=0d\omega = 0，则称 ω\omega 为一个闭形式。
  • 恰当形式 (exact)
    若 ω∈Λ(X)\omega \in \Lambda(X) 是一个微分形式 θ∈Λ(X)\theta \in \Lambda(X) 的外微分，即 ω=dθ\omega = d\theta，则称 ω\omega 为一个恰当形式。

由外微分算子的幂零性容易看出：任意恰当形式都是闭形式。

de Rham 上同调群（de Rham cohomology）

令

Zs(X)=Ker(d:Λs(X)→Λs+1(X))={ω∈Λs(X)∣dω=0}Bs(X)=Im(d:Λs−1(X)→Λs(X))={ω∈Λs(X)∣ω=dθ}\begin{aligned} &Z^ s (X) = \mathrm{Ker}(d : \Lambda _ s (X) \rightarrow \Lambda_{s+1} (X)) = \{\omega \in \Lambda_s (X)|d\omega = 0\}\\ &B^ s (X) = \mathrm{Im}(d : \Lambda_ {s-1} (X) \rightarrow \Lambda_ s (X)) = \{\omega \in \Lambda_ s (X)|\omega = d\theta\}\\ \end{aligned}

其中 θ∈Λs−1(X)\theta \in \Lambda_{s-1} (X)。显然 Zs(X)Z^ s (X) 和 Bs(X)B^ s (X) 都具有线性空间结构，当然也具有阿贝尔群结构。而且 Bs(X)B^ s (X) 是 Zs(X)Z^ s (X) 的子群。阿贝尔群的子群都是正规子群，因此我们可以考虑商群：

Hs(X)=Zs(X)/Bs(X)H^ s (X) = Z^ s (X)/B^ s (X)

称为光滑流形 XX 上的第 ss 个 de Rham 上同调群。因为它是两个线性空间的商空间，因此它还具有自然的线性空间结构。

当 s=0s=0 时，容易看出 B0≅{0}B^0\cong\{0\}，而 Z0(X)=RZ^0(X) = \mathbb{R}，若 XX 为连通的光滑流形（外微分为零的光滑函数为常函数）。因此对于连通光滑流形，我们总有：

H0(X)=RH^0(X) = \mathbb{R}

若 XX 是非连通流形，且有 kk-连通部分，则它的第零个上同调群为 H0(X)=RkH_0(X) = \mathbb{R}^k。

总结

  • 可微结构使得我们能够在流形上每一点引入一个线性空间和余切空间，这样我们可以在流形上的每一点都引入一个张量。进一步地，我们可以研究流形上的光滑张量场。
  • 到现在为止，在一个给定的光滑流形上，我们已经讨论了三种算子：李导数、外微分和内乘。它们的定义只依赖于光滑流形的微分结构。换句话说，有了微分结构之后，这些算子是可以自然定义的。在讨论它们的时候，我们不需要引入额外的数学结构。
  • 微分流形是很多其他数学结构建立的平台。在接下来的笔记中，我们将引入联络和度规。它们就是在微分流形上建立的非常有用的数学结构，在广义相对论或其他一些引力理论中都是非常重要的。