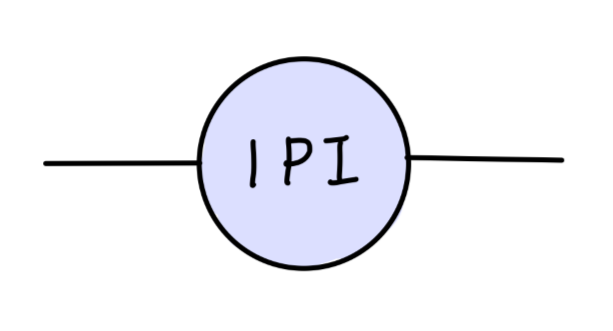
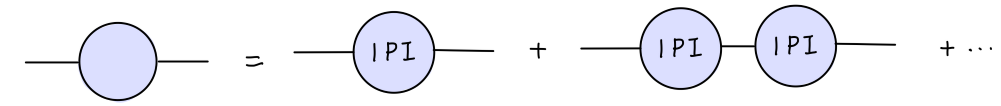上一篇中,我们讨论了对两点关联函数的傅里叶变换。我们将其看作 p 2 p^2 p 2
∫ d 4 x e i p ⋅ x ⟨ Ω ∣ T ϕ ( x ) ϕ ( 0 ) ∣ Ω ⟩ ∼ p 2 → m 2 i Z p 2 − m 2 + i ϵ (1) \int d^4x e^{ip\cdot x} \langle \Omega|T\phi(x)\phi(0)|\Omega\rangle \underset{p^2\rightarrow m^2}{\sim} \frac{iZ}{p^2-m^2+i\epsilon}\tag{1}
∫ d 4 x e i p ⋅ x ⟨ Ω ∣ T ϕ ( x ) ϕ ( 0 ) ∣ Ω ⟩ p 2 → m 2 ∼ p 2 − m 2 + i ϵ i Z ( 1 )
这一篇中,我们想要推广这个结果到高阶关联函数,并给出关联函数与散射矩阵的一般关系。相关理论由 Lehmann, Symanzik 与 Zimmermann 首先得到,被称为 LSZ 约化公式 LSZ reduction formula 。为了简单起见,我们下面以标量场为例进行说明。
例如我们想要计算 2 → n 2\rightarrow n 2 → n n + 2 n+2 n + 2 n + 2 n+2 n + 2
∫ d 4 x e i p ⋅ x ⟨ Ω ∣ T ϕ ( x ) ϕ ( z 1 ) ϕ ( z 2 ) ⋯ ∣ Ω ⟩ (2) \int d^4x e^{ip\cdot x} \langle \Omega|T\phi(x)\phi(z_1)\phi(z_2)\cdots|\Omega\rangle\tag{2}
∫ d 4 x e i p ⋅ x ⟨ Ω ∣ T ϕ ( x ) ϕ ( z 1 ) ϕ ( z 2 ) ⋯ ∣ Ω ⟩ ( 2 )
现在可以将式 ( 2 ) (2) ( 2 ) p p p p 0 p^0 p 0 x 0 x^0 x 0
x 0 < T − x^0<T_{-} x 0 < T −
T − < x 0 < T + T_{-}<x^0<T_{+} T − < x 0 < T +
x 0 > T + x^0>T_{+} x 0 > T +
其中 T − < m i n { z 1 0 , z 2 0 ⋯ } T_{-} < min\{z_1^{0},z_2^{0}\cdots\} T − < m i n { z 1 0 , z 2 0 ⋯ } T + > m a x { z 1 0 , z 2 0 ⋯ } T_{+} > max\{z_1^{0},z_2^{0}\cdots\} T + > m a x { z 1 0 , z 2 0 ⋯ } 2 2 2 p 0 p^0 p 0 exp ( i p 0 x 0 ) \exp(ip^0x^0) exp ( i p 0 x 0 ) 1 , 3 1,3 1 , 3 3 3 3 x 0 x^0 x 0 z i 0 z_i^0 z i 0 ϕ ( x ) \phi(x) ϕ ( x ) ϕ ( x ) \phi(x) ϕ ( x )
1 = ∑ λ ∫ d 3 q ( 2 π ) 3 1 2 E q ( λ ) ∣ λ q ⟩ ⟨ λ q ∣ \bm{1} = \sum_{\lambda} \int \frac{d^3q}{(2\pi)^3}\frac{1}{2E_{\bm{q}}(\lambda)}|\lambda_{\bm{q}}\rangle\langle\lambda_{\bm{q}}|
1 = λ ∑ ∫ ( 2 π ) 3 d 3 q 2 E q ( λ ) 1 ∣ λ q ⟩ ⟨ λ q ∣
这一段的关联函数可以写为:
∫ T + ∞ d x 0 ∫ d 3 x e i p 0 x 0 e − i p ⋅ x ∑ λ ∫ d 3 q ( 2 π ) 3 1 2 E q ( λ ) ⟨ Ω ∣ ϕ ( x ) ∣ λ q ⟩ ⟨ λ q ∣ T { ϕ ( z 1 ) ϕ ( z 2 ) ⋯ } ∣ Ω ⟩ = ∑ λ ∫ T + ∞ d x 0 ∫ d 3 q ( 2 π ) 3 1 2 E q ( λ ) e i p 0 x 0 e − i q 0 x 0 e − ϵ x 0 ⟨ Ω ∣ ϕ ( 0 ) ∣ λ 0 ⟩ ( 2 π ) 3 δ ( 3 ) ( p − q ) ⟨ λ q ∣ T { ϕ ( z 1 ) ϕ ( z 2 ) ⋯ } ∣ Ω ⟩ = ∑ λ 1 2 E p ( λ ) i e i ( p 0 − E p + i ϵ ) T + p 0 − E p ( λ ) + i ϵ ⟨ Ω ∣ ϕ ( 0 ) ∣ λ 0 ⟩ ⟨ λ q ∣ T { ϕ ( z 1 ) ϕ ( z 2 ) ⋯ } ∣ Ω ⟩ \begin{aligned}
&\int_{T_{+}}^{\infty}dx^0 \int d^3x e^{ip^0x^0}e^{-i\bm{p}\cdot\bm{x}}\sum_{\lambda} \int \frac{d^3q}{(2\pi)^3}\frac{1}{2E_{\bm{q}}(\lambda)}\langle\Omega|\phi(x)|\lambda_{\bm{q}}\rangle\langle\lambda_{\bm{q}}|T\{\phi(z_1)\phi(z_2)\cdots\}|\Omega\rangle\\
=& \sum_{\lambda}\int_{T_{+}}^{\infty}dx^0 \int \frac{d^3q}{(2\pi)^3}\frac{1}{2E_{\bm{q}}(\lambda)}e^{ip^0x^0}e^{-iq^0x^0}e^{-\epsilon x^0} \langle \Omega|\phi(0)|\lambda_0\rangle(2\pi)^3\delta^{(3)}(\bm{p}-\bm{q})\langle\lambda_{\bm{q}}|T\{\phi(z_1)\phi(z_2)\cdots\}|\Omega\rangle\\
=& \sum_{\lambda} \frac{1}{2E_{\bm{p}}(\lambda)}\frac{ie^{i(p^0-E_{\bm{p}}+i\epsilon)T_+}}{p^0-E_{\bm{p}}(\lambda)+i\epsilon}\langle\Omega|\phi(0)|\lambda_0\rangle\langle\lambda_{\bm{q}}|T\{\phi(z_1)\phi(z_2)\cdots\}|\Omega\rangle\\
\end{aligned}
= = ∫ T + ∞ d x 0 ∫ d 3 x e i p 0 x 0 e − i p ⋅ x λ ∑ ∫ ( 2 π ) 3 d 3 q 2 E q ( λ ) 1 ⟨ Ω ∣ ϕ ( x ) ∣ λ q ⟩ ⟨ λ q ∣ T { ϕ ( z 1 ) ϕ ( z 2 ) ⋯ } ∣ Ω ⟩ λ ∑ ∫ T + ∞ d x 0 ∫ ( 2 π ) 3 d 3 q 2 E q ( λ ) 1 e i p 0 x 0 e − i q 0 x 0 e − ϵ x 0 ⟨ Ω ∣ ϕ ( 0 ) ∣ λ 0 ⟩ ( 2 π ) 3 δ ( 3 ) ( p − q ) ⟨ λ q ∣ T { ϕ ( z 1 ) ϕ ( z 2 ) ⋯ } ∣ Ω ⟩ λ ∑ 2 E p ( λ ) 1 p 0 − E p ( λ ) + i ϵ i e i ( p 0 − E p + i ϵ ) T + ⟨ Ω ∣ ϕ ( 0 ) ∣ λ 0 ⟩ ⟨ λ q ∣ T { ϕ ( z 1 ) ϕ ( z 2 ) ⋯ } ∣ Ω ⟩
在极点 p 0 = ∣ p ∣ 2 + m 2 p^0 = \sqrt{|\bm{p}|^2+m^2} p 0 = ∣ p ∣ 2 + m 2
∫ d 4 x e i p ⋅ x ⟨ Ω ∣ T ϕ ( x ) ϕ ( z 1 ) ϕ ( z 2 ) ⋯ ∣ Ω ⟩ ∼ p 0 → + E p i p 2 − m 2 + i ϵ Z ⟨ p ∣ T { ϕ ( z 1 ) ⋯ } ∣ Ω ⟩ (3) \int d^4x e^{ip\cdot x} \langle \Omega|T\phi(x)\phi(z_1)\phi(z_2)\cdots|\Omega\rangle \underset{p^0\rightarrow + E_{\bm{p}}}{\sim} \frac{i}{p^2-m^2+i\epsilon}\sqrt{Z}\langle\bm{p}|T\{\phi(z_1)\cdots\}|\Omega\rangle\tag{3}
∫ d 4 x e i p ⋅ x ⟨ Ω ∣ T ϕ ( x ) ϕ ( z 1 ) ϕ ( z 2 ) ⋯ ∣ Ω ⟩ p 0 → + E p ∼ p 2 − m 2 + i ϵ i Z ⟨ p ∣ T { ϕ ( z 1 ) ⋯ } ∣ Ω ⟩ ( 3 )
同理,在区域 1 1 1
∫ d 4 x e i p ⋅ x ⟨ Ω ∣ T ϕ ( x ) ϕ ( z 1 ) ϕ ( z 2 ) ⋯ ∣ Ω ⟩ ∼ p 0 → − E p ⟨ Ω ∣ T { ϕ ( z 1 ) ⋯ } ∣ − p ⟩ Z i p 2 − m 2 + i ϵ (4) \int d^4x e^{ip\cdot x} \langle \Omega|T\phi(x)\phi(z_1)\phi(z_2)\cdots|\Omega\rangle \underset{p^0\rightarrow - E_{\bm{p}}}{\sim} \langle\Omega|T\{\phi(z_1)\cdots\}|-\bm{p}\rangle\sqrt{Z}\frac{i}{p^2-m^2+i\epsilon}\tag{4}
∫ d 4 x e i p ⋅ x ⟨ Ω ∣ T ϕ ( x ) ϕ ( z 1 ) ϕ ( z 2 ) ⋯ ∣ Ω ⟩ p 0 → − E p ∼ ⟨ Ω ∣ T { ϕ ( z 1 ) ⋯ } ∣ − p ⟩ Z p 2 − m 2 + i ϵ i ( 4 )
为了得到有关剩余的场量坐标 z 1 , z 2 , ⋯ z_1,z_2,\cdots z 1 , z 2 , ⋯ φ ( k ) \varphi(\bm{k}) φ ( k ) k = p \bm{k} = \bm{p} k = p
∫ d 4 x e i p 0 x 0 e − i p ⋅ x → ∫ d 3 k ( 2 π ) 3 ∫ d 4 x e i p 0 x 0 e − i k ⋅ x φ ( k ) (5) \int d^4x e^{ip^0x^0}e^{-i\bm{p}\cdot\bm{x}}\rightarrow \int \frac{d^3k}{(2\pi)^3} \int d^4x e^{ip^0x^0}e^{-i\bm{k}\cdot\bm{x}}\varphi(\bm{k})\tag{5}
∫ d 4 x e i p 0 x 0 e − i p ⋅ x → ∫ ( 2 π ) 3 d 3 k ∫ d 4 x e i p 0 x 0 e − i k ⋅ x φ ( k ) ( 5 )
当 φ ( k ) \varphi(\bm{k}) φ ( k ) δ \delta δ ( 3 ) (3) ( 3 )
∫ d 3 k ( 2 π ) 3 ∫ d 4 x e i p 0 x 0 e − i k ⋅ x φ ( k ) ⟨ Ω ∣ T ϕ ( x ) ϕ ( z 1 ) ϕ ( z 2 ) ⋯ ∣ Ω ⟩ = ∑ λ ∫ d 3 k ( 2 π ) 3 φ ( k ) 1 2 E k ( λ ) i p 0 − E k ( λ ) + i ϵ ⟨ Ω ∣ ϕ ( 0 ) ∣ λ 0 ⟩ ⟨ λ k ∣ T { ϕ ( z 1 ) ⋯ } ∣ Ω ⟩ ∼ p 0 → + E p ∫ d 3 k ( 2 π ) 3 φ ( k ) i p ~ 2 − m 2 + i ϵ Z ⟨ k ∣ T { ϕ ( z 1 ) ⋯ } ∣ Ω ⟩ \begin{aligned}
&\int \frac{d^3k}{(2\pi)^3} \int d^4x e^{ip^0x^0}e^{-i\bm{k}\cdot\bm{x}}\varphi(\bm{k}) \langle \Omega|T\phi(x)\phi(z_1)\phi(z_2)\cdots|\Omega\rangle\\
=& \sum_{\lambda}\int \frac{d^3k}{(2\pi)^3} \varphi(\bm{k}) \frac{1}{2E_{\bm{k}}(\lambda)} \frac{i}{ p^0 - E_{\bm{k}}(\lambda)+ i\epsilon}\langle \Omega|\phi(0)|\lambda_0\rangle\langle \lambda_{\bm{k}}|T\{\phi(z_1)\cdots\}|\Omega\rangle \\
\underset{p^0\rightarrow + E_{\bm{p}}}{\sim} & \int \frac{d^3k}{(2\pi)^3} \varphi(\bm{k})\frac{i}{\tilde{p}^2-m^2+i\epsilon}\sqrt{Z}\langle\bm{k}|T\{\phi(z_1)\cdots\}|\Omega\rangle\\
\end{aligned}
= p 0 → + E p ∼ ∫ ( 2 π ) 3 d 3 k ∫ d 4 x e i p 0 x 0 e − i k ⋅ x φ ( k ) ⟨ Ω ∣ T ϕ ( x ) ϕ ( z 1 ) ϕ ( z 2 ) ⋯ ∣ Ω ⟩ λ ∑ ∫ ( 2 π ) 3 d 3 k φ ( k ) 2 E k ( λ ) 1 p 0 − E k ( λ ) + i ϵ i ⟨ Ω ∣ ϕ ( 0 ) ∣ λ 0 ⟩ ⟨ λ k ∣ T { ϕ ( z 1 ) ⋯ } ∣ Ω ⟩ ∫ ( 2 π ) 3 d 3 k φ ( k ) p ~ 2 − m 2 + i ϵ i Z ⟨ k ∣ T { ϕ ( z 1 ) ⋯ } ∣ Ω ⟩
其中 p ~ = ( p 0 , k ) \tilde{p} = (p_0,\bm{k}) p ~ = ( p 0 , k ) ( n + 2 ) (n+2) ( n + 2 )
( ∏ i ∫ d 3 k i ( 2 π ) 3 ∫ d 4 x i e i p ~ i ⋅ x i φ i ( k i ) ) ⟨ Ω ∣ T { ϕ ( x 1 ) ϕ ( x 2 ) ⋯ } ∣ Ω ⟩ (6) (\prod_i\int\frac{d^3k_i}{(2\pi)^3}\int d^4x_i e^{i \tilde{p}_i\cdot x_i}\varphi_i(\bm{k}_i))\langle\Omega|T\{\phi(x_1)\phi(x_2)\cdots\}|\Omega\rangle \tag{6}
( i ∏ ∫ ( 2 π ) 3 d 3 k i ∫ d 4 x i e i p ~ i ⋅ x i φ i ( k i ) ) ⟨ Ω ∣ T { ϕ ( x 1 ) ϕ ( x 2 ) ⋯ } ∣ Ω ⟩ ( 6 )
我们在 x = 0 x = 0 x = 0 x i 0 < T − x_i^0 < T_{-} x i 0 < T − x i 0 > T + x_i^0 > T_{+} x i 0 > T + x i 0 x_i^0 x i 0
x i 0 < T − x_i^0<T_{-} x i 0 < T −
T − < x i 0 < T + T_{-}<x_i^0<T_{+} T − < x i 0 < T +
x i 0 > T + x_i^0>T_{+} x i 0 > T +
对于区域 2 2 2 p i 0 p_i^0 p i 0 1 , 3 1,3 1 , 3 x i 0 x_i^0 x i 0 1 1 1 3 3 3 x 1 x_1 x 1 x 2 x_2 x 2 3 3 3 1 1 1
T { ϕ ( x 1 ) ϕ ( x 2 ) ϕ ( x 3 ) ⋯ } = T { ϕ ( x 1 ) ϕ ( x 2 ) } T { ϕ ( x 3 ) ⋯ } T\{\phi(x_1)\phi(x_2)\phi(x_3)\cdots\} = T\{\phi(x_1)\phi(x_2)\}T\{\phi(x_3)\cdots\}
T { ϕ ( x 1 ) ϕ ( x 2 ) ϕ ( x 3 ) ⋯ } = T { ϕ ( x 1 ) ϕ ( x 2 ) } T { ϕ ( x 3 ) ⋯ }
设两粒子本征态为 λ K \lambda_{\bm{K}} λ K
( 1 ) t w o p a r t i c l e s = ∑ λ ∫ d 3 K ( 2 π ) 3 1 2 E K ∣ λ K ⟩ ⟨ λ K ∣ (\bm{1})_{two\ particles} = \sum_{\lambda} \int \frac{d^3K}{(2\pi)^3}\frac{1}{2E_{\bm{K}}}|\lambda_{\bm{K}}\rangle\langle\lambda_{\bm{K}}|
( 1 ) t w o p a r t i c l e s = λ ∑ ∫ ( 2 π ) 3 d 3 K 2 E K 1 ∣ λ K ⟩ ⟨ λ K ∣
对该 ( n + 2 ) (n+2) ( n + 2 ) x 1 , x 2 x_1,x_2 x 1 , x 2
∑ λ ∫ d 3 K ( 2 π ) 3 1 2 E K ( ∏ i = 1 , 2 ∫ d 3 k i ( 2 π ) 3 ∫ d 4 x i e i p ~ i ⋅ x i φ i ( k i ) ) × ⟨ Ω ∣ T { ϕ ( x 1 ) ϕ ( x 2 ) } ∣ λ K ⟩ ⟨ λ K ∣ T { ϕ ( x 3 ) ⋯ } ∣ Ω ⟩ (7) \begin{aligned}
\sum_{\lambda} \int \frac{d^3K}{(2\pi)^3}\frac{1}{2E_{\bm{K}}} (&\prod_{i=1,2}\int\frac{d^3k_i}{(2\pi)^3}\int d^4x_i e^{i \tilde{p}_i\cdot x_i}\varphi_i(\bm{k}_i))\\
&\times \langle\Omega|T\{\phi(x_1)\phi(x_2)\}|\lambda_{\bm{K}}\rangle\langle\lambda_{\bm{K}}|T\{\phi(x_3)\cdots\}|\Omega\rangle\\
\end{aligned}\tag{7}
λ ∑ ∫ ( 2 π ) 3 d 3 K 2 E K 1 ( i = 1 , 2 ∏ ∫ ( 2 π ) 3 d 3 k i ∫ d 4 x i e i p ~ i ⋅ x i φ i ( k i ) ) × ⟨ Ω ∣ T { ϕ ( x 1 ) ϕ ( x 2 ) } ∣ λ K ⟩ ⟨ λ K ∣ T { ϕ ( x 3 ) ⋯ } ∣ Ω ⟩ ( 7 )
若 λ K \lambda_{\bm{K}} λ K λ K \lambda_{\bm{K}} λ K
∣ λ K ⟩ = ∣ λ q 1 ⟩ ∣ λ q 2 ⟩ |\lambda_{\bm{K}}\rangle = |\lambda_{\bm{q}_1}\rangle|\lambda_{\bm{q}_2}\rangle
∣ λ K ⟩ = ∣ λ q 1 ⟩ ∣ λ q 2 ⟩
并且可以将时序符号去掉(无因果性)。
如此,我们可以将 ( 7 ) (7) ( 7 )
∑ λ 1 , λ 2 ∫ d 3 q 1 ( 2 π ) 3 1 2 E q 1 ∫ d 3 q 2 ( 2 π ) 3 1 2 E q 2 ( ∏ i = 1 , 2 ∫ d 3 k i ( 2 π ) 3 ∫ d 4 x i e i p ~ i ⋅ x i φ i ( k i ) ) × ⟨ Ω ∣ ϕ ( x 1 ) ∣ λ q 1 ⟩ ⟨ Ω ∣ ϕ ( x 1 ) ∣ λ q 2 ⟩ ⟨ λ q 1 λ q 2 ∣ T { ϕ ( x 3 ) ⋯ } ∣ Ω ⟩ ∼ k i 0 → E k i ( ∏ i = 1 , 2 ∫ d 3 k i ( 2 π ) 3 φ i ( k i ) i p ~ i 2 − m 2 + i ϵ ⋅ Z ) ⟨ k 1 k 2 ∣ T { ϕ ( x 3 ) ⋯ } ∣ Ω ⟩ (8) \begin{aligned}
&\sum_{\lambda_1,\lambda_2} \int \frac{d^3q_1}{(2\pi)^3}\frac{1}{2E_{\bm{q_1}}}\int \frac{d^3q_2}{(2\pi)^3}\frac{1}{2E_{\bm{q_2}}} (\prod_{i=1,2}\int\frac{d^3k_i}{(2\pi)^3}\int d^4x_i e^{i \tilde{p}_i\cdot x_i}\varphi_i(\bm{k}_i))\\
&\times \langle\Omega|\phi(x_1)|\lambda_{\bm{q_1}}\rangle\langle\Omega|\phi(x_1)|\lambda_{\bm{q_2}}\rangle\langle\lambda_{\bm{q}_1}\lambda_{\bm{q}_2}|T\{\phi(x_3)\cdots\}|\Omega\rangle\\
\underset{\bm{k}_i^0\rightarrow E_{\bm{k}_i}}{\sim}& (\prod_{i=1,2} \int \frac{d^3k_i}{(2\pi)^3}\varphi_i(\bm{k}_i)\frac{i}{\tilde{p}_i^2-m^2+i\epsilon}\cdot \sqrt{Z})\langle \bm{k}_1\bm{k}_2|T\{\phi(x_3)\cdots\}|\Omega\rangle\\
\end{aligned}\tag{8}
k i 0 → E k i ∼ λ 1 , λ 2 ∑ ∫ ( 2 π ) 3 d 3 q 1 2 E q 1 1 ∫ ( 2 π ) 3 d 3 q 2 2 E q 2 1 ( i = 1 , 2 ∏ ∫ ( 2 π ) 3 d 3 k i ∫ d 4 x i e i p ~ i ⋅ x i φ i ( k i ) ) × ⟨ Ω ∣ ϕ ( x 1 ) ∣ λ q 1 ⟩ ⟨ Ω ∣ ϕ ( x 1 ) ∣ λ q 2 ⟩ ⟨ λ q 1 λ q 2 ∣ T { ϕ ( x 3 ) ⋯ } ∣ Ω ⟩ ( i = 1 , 2 ∏ ∫ ( 2 π ) 3 d 3 k i φ i ( k i ) p ~ i 2 − m 2 + i ϵ i ⋅ Z ) ⟨ k 1 k 2 ∣ T { ϕ ( x 3 ) ⋯ } ∣ Ω ⟩ ( 8 )
现在令 φ ( k i ) \varphi(\bm{k}_i) φ ( k i ) δ \delta δ
( ∏ i = 1 , 2 i p i 2 − m 2 + i ϵ ⋅ Z ) ⟨ p 1 p 2 ∣ T { ϕ ( x 3 ) ⋯ } ∣ Ω ⟩ (\prod_{i=1,2} \frac{i}{p_i^2-m^2+i\epsilon}\cdot \sqrt{Z})\langle \bm{p}_1\bm{p}_2|T\{\phi(x_3)\cdots\}|\Omega\rangle
( i = 1 , 2 ∏ p i 2 − m 2 + i ϵ i ⋅ Z ) ⟨ p 1 p 2 ∣ T { ϕ ( x 3 ) ⋯ } ∣ Ω ⟩
对于处于区域 1 1 1 x 3 , ⋯ x_3,\cdots x 3 , ⋯
( ∏ i = 1 , 2 i p i 2 − m 2 + i ϵ ⋅ Z ) ( ∏ i = 3 , ⋯ i p i 2 − m 2 + i ϵ ⋅ Z ) o u t ⟨ p 1 p 2 ∣ − p 3 ⋯ ⟩ i n (\prod_{i=1,2} \frac{i}{p_i^2-m^2+i\epsilon}\cdot \sqrt{Z})(\prod_{i=3,\cdots} \frac{i}{p_i^2-m^2+i\epsilon}\cdot \sqrt{Z})_{out}\langle \bm{p}_1\bm{p}_2|-\bm{p}_3\cdots\rangle_{in}
( i = 1 , 2 ∏ p i 2 − m 2 + i ϵ i ⋅ Z ) ( i = 3 , ⋯ ∏ p i 2 − m 2 + i ϵ i ⋅ Z ) o u t ⟨ p 1 p 2 ∣ − p 3 ⋯ ⟩ i n
最后一项不是别的,正是散射矩阵!我们将这个结果一般化:
∏ 1 n ∫ d 4 x i e i p i ⋅ x i ∏ 1 m ∫ d 4 y i e − i k i ⋅ y i ⟨ Ω ∣ T { ϕ ( x 1 ) ⋯ ϕ ( x n ) ϕ ( y 1 ) ⋯ ϕ ( y m ) } ∣ Ω ⟩ ∼ p i 0 → E p i , k i 0 → E k i ( ∏ i = 1 n Z i p i 2 − m 2 + i ϵ ) ( ∏ j = 1 m Z i k j 2 − m 2 + i ϵ ) ⟨ p 1 ⋯ p n ∣ S ∣ k 1 ⋯ k m ⟩ (9) \begin{aligned}
&\prod_{1}^{n}\int d^4x_i e^{ip_i\cdot x_i} \prod_{1}^{m}\int d^4y_i e^{-ik_i\cdot y_i}\langle\Omega|T\{\phi(x_1)\cdots \phi(x_n)\phi(y_1)\cdots \phi(y_m)\}|\Omega\rangle\\
\underset{\bm{p}_i^0\rightarrow E_{\bm{p}_i},\bm{k}_i^0\rightarrow E_{\bm{k}_i}}{\sim}& (\prod_{i=1}^{n} \frac{\sqrt{Z} i}{p_i^2-m^2+i\epsilon})(\prod_{j=1}^{m} \frac{\sqrt{Z} i}{k_j^2-m^2+i\epsilon})\langle \bm{p}_1\cdots \bm{p}_n|S|\bm{k}_1\cdots\bm{k}_m\rangle \tag{9}
\end{aligned}
p i 0 → E p i , k i 0 → E k i ∼ 1 ∏ n ∫ d 4 x i e i p i ⋅ x i 1 ∏ m ∫ d 4 y i e − i k i ⋅ y i ⟨ Ω ∣ T { ϕ ( x 1 ) ⋯ ϕ ( x n ) ϕ ( y 1 ) ⋯ ϕ ( y m ) } ∣ Ω ⟩ ( i = 1 ∏ n p i 2 − m 2 + i ϵ Z i ) ( j = 1 ∏ m k j 2 − m 2 + i ϵ Z i ) ⟨ p 1 ⋯ p n ∣ S ∣ k 1 ⋯ k m ⟩ ( 9 )
这就是 LSZ 约化公式 。它给出了一种计算散射矩阵的方法:对关联函数做合适的傅里叶变换,并找到在对应的多粒子态 mass shell 附近的系数。
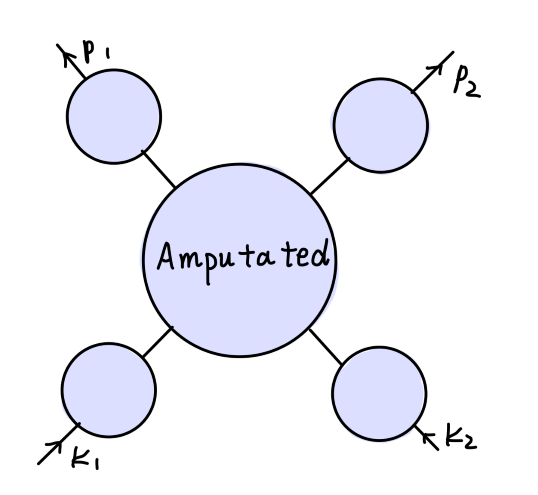
下面结合费曼图对式 ( 9 ) (9) ( 9 ) − i M 2 ( p 2 ) -iM^2(p^2) − i M 2 ( p 2 )
那么考虑如下图的值:
计算结果为:
i p 2 − m 0 2 − M 2 ( p 2 ) ∼ p 0 → E p i Z p 2 − m 2 \frac{i}{p^2 - m_0^2 - M^2(p^2)} \underset{p^0\rightarrow E_{\bm{p}}}{\sim} \frac{iZ}{p^2-m^2}
p 2 − m 0 2 − M 2 ( p 2 ) i p 0 → E p ∼ p 2 − m 2 i Z
对于一个四点关联函数来说,其对应的费曼图为:
其将包含如下的结构:
i Z p 1 2 − m 2 i Z p 2 2 − m 2 i Z k 1 2 − m 2 i Z k 2 2 − m 2 \frac{iZ}{p_1^2-m^2}\frac{iZ}{p_2^2-m^2}\frac{iZ}{k_1^2-m^2}\frac{iZ}{k_2^2-m^2}
p 1 2 − m 2 i Z p 2 2 − m 2 i Z k 1 2 − m 2 i Z k 2 2 − m 2 i Z
与 LSZ 理论相比较,得到:
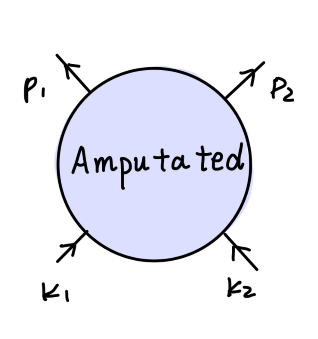
⟨ p 1 p 2 ∣ S ∣ k 1 k 2 ⟩ = ( Z ) 4 i M a m p u t a t e d \langle \bm{p}_1\bm{p}_2|S|\bm{k}_1\bm{k}_2\rangle = (\sqrt{Z})^{4}i\mathcal{M}_{amputated}
⟨ p 1 p 2 ∣ S ∣ k 1 k 2 ⟩ = ( Z ) 4 i M a m p u t a t e d
其中 i M a m p u t a t e d i\mathcal{M}_{amputated} i M a m p u t a t e d
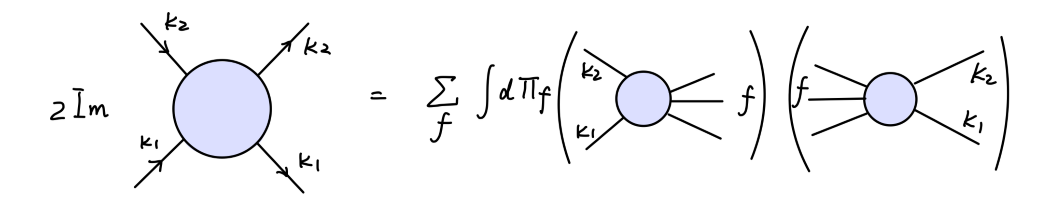
在 量子场论笔记(九):散射矩阵 中利用散射矩阵的幺正性,我们给出了光学定理。这里再用费曼图的语言进行简单说明。
利用散射矩阵的幺正性 S † S = 1 S^\dagger S =1 S † S = 1
S = 1 + i T − i ( T − T † ) = T † T \begin{aligned}
S &= 1+iT\\
-i(T-T^\dagger) &= T^\dagger T\\
\end{aligned}
S − i ( T − T † ) = 1 + i T = T † T
左右两边分别用出射态、入射态作用,最后结果为:
− i [ M ( a → b ) − M ∗ ( b → a ) ] = ∑ f ∫ d Π f M ∗ ( b → f ) M ( a → f ) (10) -i[\mathcal{M}(a\rightarrow b) - \mathcal{M}^*(b\rightarrow a)] = \sum_f \int d\Pi_f \mathcal{M}^*(b\rightarrow f)\mathcal{M}(a\rightarrow f)\tag{10}
− i [ M ( a → b ) − M ∗ ( b → a ) ] = f ∑ ∫ d Π f M ∗ ( b → f ) M ( a → f ) ( 1 0 )
用费曼图表示为:
对于费曼图对散射矩阵的贡献,其大部分情况下都是实的。除非当其中某些粒子在壳时,分母中引入的 i ϵ i\epsilon i ϵ M \mathcal{M} M s = E c m 2 s = E_{cm}^2 s = E c m 2 M \mathcal{M} M s s s s 0 s_0 s 0 s < s 0 , s ∈ R s < s_0,s\in\mathbb{R} s < s 0 , s ∈ R M ( s ) \mathcal{M}(s) M ( s ) M \mathcal{M} M
M ( s ) = [ M ( s ∗ ) ] ∗ (11) \mathcal{M}(s) = [\mathcal{M}(s^*)]^*\tag{11}
M ( s ) = [ M ( s ∗ ) ] ∗ ( 1 1 )
两边均为 s s s
R e M ( s + i ϵ ) = R e M ( s − i ϵ ) R e M ( s + i ϵ ) = − I m M ( s − i ϵ ) (12) \begin{aligned}
&\mathrm{Re}\mathcal{M}(s+i\epsilon) = \mathrm{Re}\mathcal{M}(s-i\epsilon)\\
&\mathrm{Re}\mathcal{M}(s+i\epsilon) = - \mathrm{Im}\mathcal{M}(s-i\epsilon)\\
\end{aligned}\tag{12}
R e M ( s + i ϵ ) = R e M ( s − i ϵ ) R e M ( s + i ϵ ) = − I m M ( s − i ϵ ) ( 1 2 )
因此在 s ⩾ s 0 s\geqslant s_0 s ⩾ s 0
D i s c M ( s ) = M ( s + i ϵ ) − M ( s − i ϵ ) = 2 i I m M ( s + i ϵ ) (13) \begin{aligned}
\mathrm{Disc}\mathcal{M}(s) &= \mathcal{M}(s+i\epsilon) - \mathcal{M}(s-i\epsilon)\\
&= 2i\mathrm{Im}\mathcal{M}(s+i\epsilon)\\
\end{aligned}\tag{13}
D i s c M ( s ) = M ( s + i ϵ ) − M ( s − i ϵ ) = 2 i I m M ( s + i ϵ ) ( 1 3 )
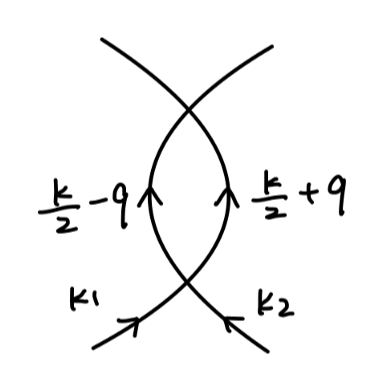
下面以 ϕ 4 \phi^4 ϕ 4 M \mathcal{M} M
费曼图
考虑一个在 s-channel 上具有一个圈的费曼图。
通过 wick rotation,该费曼图的值写为:
i δ M = λ 2 2 ∫ d 4 q ( 2 π ) 4 1 ( k / 2 − q ) 2 − m 2 + i ϵ 1 ( k / 2 + q ) 2 − m 2 + i ϵ (14) \begin{aligned}
i\delta \mathcal{M} = \frac{\lambda^2}{2}\int \frac{d^4q}{(2\pi)^4} \frac{1}{(k/2-q)^2 - m^2 + i\epsilon}\frac{1}{(k/2+q)^2 - m^2 + i\epsilon}\tag{14}
\end{aligned}
i δ M = 2 λ 2 ∫ ( 2 π ) 4 d 4 q ( k / 2 − q ) 2 − m 2 + i ϵ 1 ( k / 2 + q ) 2 − m 2 + i ϵ 1 ( 1 4 )
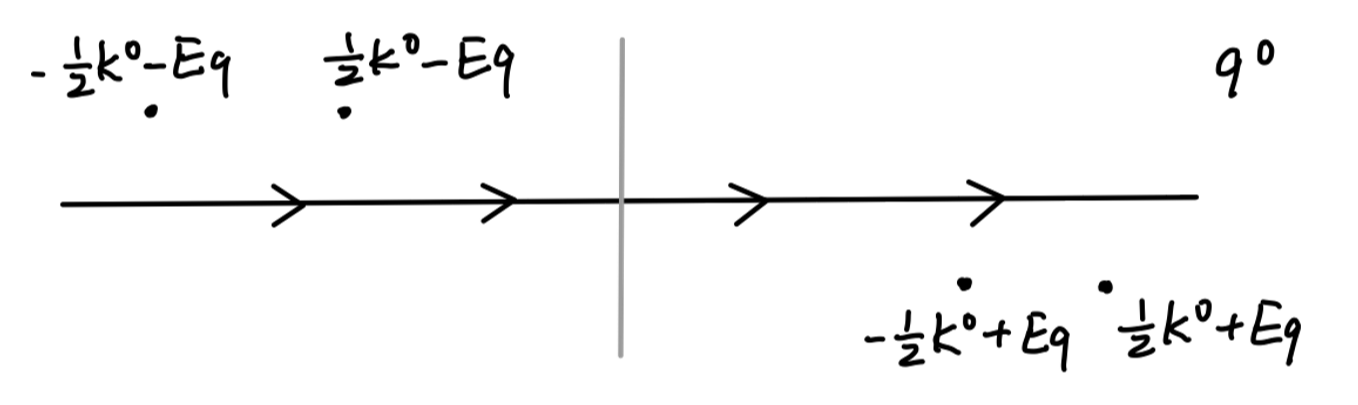
不妨在质心系中考虑问题,此时取 k = ( k 0 , 0 ) k = (k^0,\bm{0}) k = ( k 0 , 0 )
q 0 = 1 2 k 0 ± ( E q − i ϵ ) q 0 = − 1 2 k 0 ± ( E q − i ϵ ) \begin{aligned}
q^0 = \frac{1}{2}k^0 \pm (E_{\bm{q}} -i\epsilon)\\
q^0 = -\frac{1}{2}k^0 \pm (E_{\bm{q}} -i\epsilon)\\
\end{aligned}
q 0 = 2 1 k 0 ± ( E q − i ϵ ) q 0 = − 2 1 k 0 ± ( E q − i ϵ )
我们选取积分围线向下闭合。如此以下有两个极点被包括:
q 0 = ± 1 2 k 0 + E q − i ϵ q^0 = \pm\frac{1}{2}k^0 + E_{\bm{q}} -i\epsilon
q 0 = ± 2 1 k 0 + E q − i ϵ
其中,只有极点 q 0 = − 1 2 k 0 + E q − i ϵ q^0 = -\frac{1}{2}k^0 + E_{\bm{q}} -i\epsilon q 0 = − 2 1 k 0 + E q − i ϵ
i δ M = − 2 π i λ 2 2 ∫ d 3 q ( 2 π ) 4 1 2 E q 1 ( k 0 − E q ) 2 − E q 2 = − 2 π i λ 2 2 ∫ d 3 q ( 2 π ) 4 1 2 E q 1 ( k 0 − E q ) 2 − E q 2 = − 2 π i λ 2 2 4 π ( 2 π ) 4 ∫ m ∞ d E q E q ∣ q ∣ 1 2 E q 1 k 0 ( k 0 − 2 E q ) (15) \begin{aligned}
i\delta \mathcal{M} &= -2\pi i\frac{\lambda^2}{2}\int \frac{d^3q}{(2\pi)^4}\frac{1}{2E_{\bm{q}}}\frac{1}{(k^0-E_{\bm{q}})^2 - E_{\bm{q}}^2}\\
&= -2\pi i\frac{\lambda^2}{2}\int \frac{d^3q}{(2\pi)^4}\frac{1}{2E_{\bm{q}}}\frac{1}{(k^0-E_{\bm{q}})^2 - E_{\bm{q}}^2}\\
&= -2\pi i\frac{\lambda^2}{2}\frac{4\pi}{(2\pi)^4}\int_{m}^{\infty} dE_{\bm{q}}E_{\bm{q}}|\bm{q}| \frac{1}{2E_{\bm{q}}}\frac{1}{k^0(k^0-2E_{\bm{q}})}\\
\end{aligned}\tag{15}
i δ M = − 2 π i 2 λ 2 ∫ ( 2 π ) 4 d 3 q 2 E q 1 ( k 0 − E q ) 2 − E q 2 1 = − 2 π i 2 λ 2 ∫ ( 2 π ) 4 d 3 q 2 E q 1 ( k 0 − E q ) 2 − E q 2 1 = − 2 π i 2 λ 2 ( 2 π ) 4 4 π ∫ m ∞ d E q E q ∣ q ∣ 2 E q 1 k 0 ( k 0 − 2 E q ) 1 ( 1 5 )
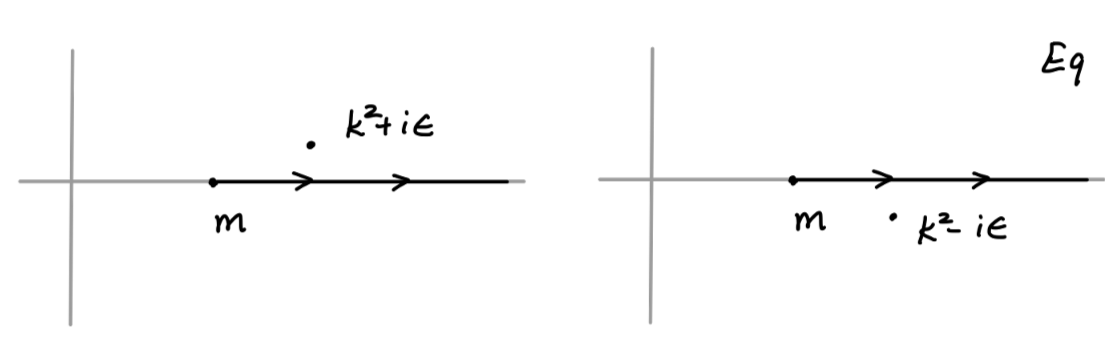
应用留数定理的过程等价于作如下替代:
1 ( k / 2 + q ) 2 − m 2 + i ϵ → − 2 π i δ ( ( k / 2 + q ) 2 − m 2 ) \frac{1}{(k/2+q)^2-m^2+i\epsilon} \rightarrow -2\pi i\delta((k/2+q)^2-m^2)
( k / 2 + q ) 2 − m 2 + i ϵ 1 → − 2 π i δ ( ( k / 2 + q ) 2 − m 2 )
最后一行表达式中出现了有关 E q E_{\bm{q}} E q E q = k 0 / 2 E_{\bm{q}} = k_0/2 E q = k 0 / 2 E q E_{\bm{q}} E q m m m k 0 < 2 m k_0 < 2m k 0 < 2 m E q E_{\bm{q}} E q k 0 2 \frac{k^0}{2} 2 k 0 k 0 > 2 m k^0 > 2m k 0 > 2 m
应用以下公式:
1 k 0 − 2 E q ± i ϵ = P 1 k 0 − 2 E q ∓ i π δ ( k 0 − 2 E q ) \frac{1}{k^0 - 2E_{\bm{q}} \pm i\epsilon} = P\frac{1}{k^0 - 2E_{\bm{q}}} \mp i\pi \delta(k^0-2E_{\bm{q}})
k 0 − 2 E q ± i ϵ 1 = P k 0 − 2 E q 1 ∓ i π δ ( k 0 − 2 E q )
其中不连续的部分来自于 δ \delta δ δ M \delta M δ M
1 ( k / 2 − q ) 2 − m 2 + i ϵ → − 2 π i δ ( ( k / 2 − q ) 2 − m 2 ) \frac{1}{(k/2-q)^2-m^2+i\epsilon} \rightarrow -2\pi i\delta((k/2-q)^2-m^2)
( k / 2 − q ) 2 − m 2 + i ϵ 1 → − 2 π i δ ( ( k / 2 − q ) 2 − m 2 )
再次回到 ( 15 ) (15) ( 1 5 )
i δ M = λ 2 2 ∫ d 4 p 1 ( 2 π ) 4 ∫ d 4 p 2 ( 2 π ) 4 1 p 1 2 − m 2 + i ϵ 1 p 2 2 − m 2 + i ϵ δ ( 4 ) ( p 1 + p 2 − k ) i\delta \mathcal{M} = \frac{\lambda^2}{2}\int \frac{d^4p_1}{(2\pi)^4}\int \frac{d^4p_2}{(2\pi)^4} \frac{1}{p_1^2 - m^2 + i\epsilon}\frac{1}{p_2^2 - m^2 + i\epsilon}\delta^{(4)}(p_1+p_2-k)
i δ M = 2 λ 2 ∫ ( 2 π ) 4 d 4 p 1 ∫ ( 2 π ) 4 d 4 p 2 p 1 2 − m 2 + i ϵ 1 p 2 2 − m 2 + i ϵ 1 δ ( 4 ) ( p 1 + p 2 − k )
为了计算 δ M \delta \mathcal{M} δ M
1 p i 2 − m 2 + i ϵ → − 2 π i δ ( p i 2 − m 2 ) (16) \frac{1}{p_i^2-m^2+i\epsilon} \rightarrow -2\pi i\delta(p_i^2-m^2)\tag{16}
p i 2 − m 2 + i ϵ 1 → − 2 π i δ ( p i 2 − m 2 ) ( 1 6 )
得到:
i δ M = − λ 2 2 ∫ d 3 p 1 ( 2 π ) 3 1 2 E 1 ∫ d 3 p 2 ( 2 π ) 3 1 2 E 2 δ ( 4 ) ( p 1 + p 2 − k ) i\delta \mathcal{M} = -\frac{\lambda^2}{2}\int \frac{d^3p_1}{(2\pi)^3}\frac{1}{2E_1} \int \frac{d^3p_2}{(2\pi)^3} \frac{1}{2E_2}\delta^{(4)}(p_1+p_2-k)
i δ M = − 2 λ 2 ∫ ( 2 π ) 3 d 3 p 1 2 E 1 1 ∫ ( 2 π ) 3 d 3 p 2 2 E 2 1 δ ( 4 ) ( p 1 + p 2 − k )
其中,λ 2 \lambda^2 λ 2
∣ M ( k ) ∣ 2 = λ 2 |\mathcal{M}(k)|^2 = \lambda^2
∣ M ( k ) ∣ 2 = λ 2
因此有:
D i s c M ( k ) = i 2 ∫ d 3 p 1 ( 2 π ) 3 1 2 E 1 ∫ d 3 p 2 ( 2 π ) 3 1 2 E 2 ∣ M ( k ) ∣ 2 δ ( 4 ) ( p 1 + p 2 − k ) \mathrm{Disc}\mathcal{M}(k) = \frac{i}{2}\int \frac{d^3p_1}{(2\pi)^3}\frac{1}{2E_1} \int \frac{d^3p_2}{(2\pi)^3} \frac{1}{2E_2} |\mathcal{M}(k)|^2 \delta^{(4)}(p_1+p_2-k)
D i s c M ( k ) = 2 i ∫ ( 2 π ) 3 d 3 p 1 2 E 1 1 ∫ ( 2 π ) 3 d 3 p 2 2 E 2 1 ∣ M ( k ) ∣ 2 δ ( 4 ) ( p 1 + p 2 − k )
到此在 ϕ 4 \phi^4 ϕ 4 ( 10 ) (10) ( 1 0 )
Cutkosky 证明了如下计算不连续性的普遍方法:
将费曼图进行所有可能的分割,使得被分割的传播子能够同时在壳。
对于每一个被分割的传播子,做替代 1 / ( p i 2 − m 2 + i ϵ ) → − 2 π i δ ( p i 2 − m 2 ) 1/(p_i^2-m^2+i\epsilon) \rightarrow -2\pi i\delta(p_i^2-m^2) 1 / ( p i 2 − m 2 + i ϵ ) → − 2 π i δ ( p i 2 − m 2 )
将所有可能的分割方式的贡献求和。
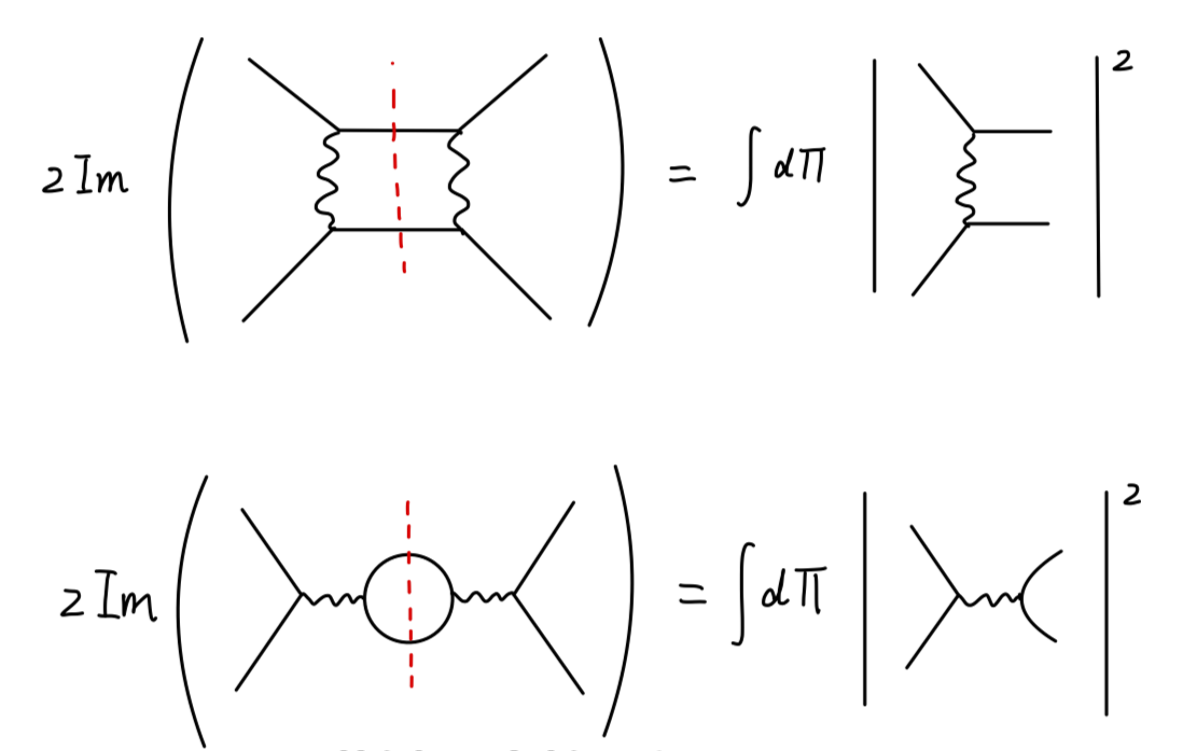
以 Bhabha 散射为例,根据光学定理有:
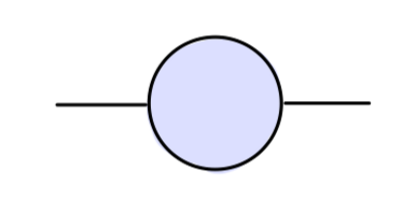
下面我们应用光学定理处理关于一个标量粒子的两点关联函数:
其值为:
i p 2 − m 0 2 − M 2 ( p 2 ) \frac{i}{p^2-m_0^2-M^2(p^2)}
p 2 − m 0 2 − M 2 ( p 2 ) i
利用 LSZ 约化公式,有:
M ( p → p ) = − Z M 2 ( p 2 ) (17) \mathcal{M}(p\rightarrow p) = -ZM^2(p^2)\tag{17}
M ( p → p ) = − Z M 2 ( p 2 ) ( 1 7 )
对于这个标量粒子是稳定的情况(不发生衰变),那么将没有可能的末态对 ( 10 ) (10) ( 1 0 ) M 2 ( p 2 ) M^2(p^2) M 2 ( p 2 )
m 2 − m 0 2 − M 2 ( m 2 ) = 0 (18) m^2 - m_0^2 -M^2(m^2) = 0 \tag{18}
m 2 − m 0 2 − M 2 ( m 2 ) = 0 ( 1 8 )
将具有一个实值极点 m m m
对于这个标量粒子不稳定的情况(粒子可以发生衰变,生成多个更轻的粒子),M 2 ( p 2 ) M^2(p^2) M 2 ( p 2 ) ( 18 ) (18) ( 1 8 )
m 2 − m 0 2 − R e M 2 ( m 2 ) = 0 (19) m^2 - m_0^2 - \mathrm{Re} M^2(m^2) = 0 \tag{19}
m 2 − m 0 2 − R e M 2 ( m 2 ) = 0 ( 1 9 )
如此,我们可以得到:
i Z p 2 − m 2 − i Z I m M 2 ( p 2 ) (20) \frac{iZ}{p^2-m^2 - iZ\mathrm{Im}M^2(p^2)} \tag{20}
p 2 − m 2 − i Z I m M 2 ( p 2 ) i Z ( 2 0 )
在极点附近,散射截面将具有形式:
σ ∝ ∣ 1 s − m 2 − i Z I m M 2 ( p 2 ) ∣ \sigma\propto |\frac{1}{s-m^2-iZ\mathrm{Im}M^2(p^2)}|
σ ∝ ∣ s − m 2 − i Z I m M 2 ( p 2 ) 1 ∣
根据 Breit-Wigner 公式,在共振态附近的散射截面为:
σ ∝ ∣ 1 p 2 − m 2 + i m Γ ∣ 2 \sigma \propto |\frac{1}{p^2-m^2+im\Gamma}|^2
σ ∝ ∣ p 2 − m 2 + i m Γ 1 ∣ 2
那么可以得到衰变速率的表达式:
Γ = − Z m I m M 2 ( m 2 ) (21) \Gamma = -\frac{Z}{m}\mathrm{Im}M^2(m^2) \tag{21}
Γ = − m Z I m M 2 ( m 2 ) ( 2 1 )
这个表达式根据 ( 10 ) (10) ( 1 0 )
Γ = 1 2 m ∑ f ∫ d Π f ∣ M ( p → f ) ∣ 2 (22) \Gamma = \frac{1}{2m}\sum_f\int d\Pi_f |\mathcal{M}(p\rightarrow f)|^2 \tag{22}
Γ = 2 m 1 f ∑ ∫ d Π f ∣ M ( p → f ) ∣ 2 ( 2 2 )